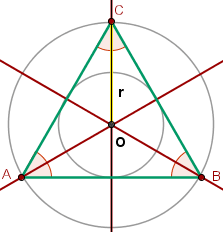
Нарисуйте равносторонний треугольник с заданным центром

в данный момент я могу ответить только на ваш второй вопрос. Просто сделай тест пересечения точек, при условии, что вы сохранили очки, которые определяют ваш треугольник. Вы можете найти много относительных алгоритмов в книгах по компьютерной графике.

редактировать: Я подумал о методологии решения вашей основной проблемы (найдите 3 точки, которые определяют равносторонний треугольник с CX, cy и радиусом в качестве данных). Он полагается на свойство, что сумма 3 углов любой треугольник равен 180 градусам. Мне нужно некоторое время, чтобы сделать дополнительную проверку, чтобы убедиться, что это правильно. Затем я отредактирую свой ответ, чтобы опубликовать его.

Edit-Полный Ответ: реализация этого алгоритмического эскиза основывается на выбранном вами языке программирования и графическом API:

• переведите центр 2D-системы координат (предположим, что он по часовой стрелке) в центр центроидной окружности.
• хранить 2 точки, которые определяют 2 отрезки прямой линии, вместе с центр круга. Объединение этих сегментов может дать вам диаметр круга. Оба сегмента имеют центр круг как их 1 определяющая точка. Другие 2 определяющие точки (которые необходимо сохранить) на окружности (используйте радиус длины окружности, чтобы найти их).
• Поверните 2 точки На окружность на 60 градусов, одну из них по часовой стрелке и против часовой стрелки. Хранить их новый координирует. Нарисуйте линию, которая их соединяет. У вас есть 2 из 3 вершины треугольника.
• выполните обратный перевод центра системы координат.
• оставшаяся вершина треугольника является точкой пересечения радиус окружности и два отрезка линии, каждый из которых начинается со своего соответствующая известная вершина треугольника.
• наконец, сохраните вершины и нарисуйте треугольник.

надеюсь, это поможет. Я попытаюсь добавить некоторые чертежи, чтобы уточнить немного больше шагов этой методологии. Кроме того, я запрограммирую и протестирую эти шаги, чтобы убедиться, что правильно решить вашу проблему.

мне нужно было нарисовать равносторонний треугольник с помощью SVG и Javascript...

Я попытался ответить на первый вопрос Ксантикса, чтобы построить равносторонний треугольник с заданной центральной точкой (cx,cy) и радиусом окружности (r), который, как было указано, легко решает координаты точки C (cx, cy + r).

однако я не мог понять, как получить уравнения вращения для решения любых координат для точек A & B, поэтому мое решение таково: следует.

математическое время-решить для x

предположим, что cx = 9, cy = 9, r = 6 и горизонтальное основание.

сначала найдите длину сторон треугольника (a,b, c):

9r^2 = a^2 + b^2 + c^2

r^2 = 36, 9r^2 = 324, 324/3 = 108, sqrt(432) = 10.39

как только мы узнаем длину каждой стороны треугольника (s = 10.39), мы можем вычислить координаты X. Добавить s/2 (5.2) в cx для Bx (14.2) и вычесть s / 2 из cx для Ax (3.8).

X решено теперь нужно y

говоря о s / 2, если мы разделим треугольник пополам вертикально (от точки C до середины между точками A & B), мы можем решить для y (в конечном счете, давая нам Ay и By):

a^2 + b^2 = c^2

a^2 + 27.04 (1/2 s squared) = 107.95 (length s squared)

a^2 = 80.91

sqrt(80.91) = 8.99

вычесть это значение y из cy + r (15 - 8.99 = 6.01) дает нам наш новый график y для обеих точек A и B.

Center ( 9.00, 9.00)
C      ( 9.00,15.00)
B      (14.20, 6.01)
A      ( 3.80, 6.01)

вывод

как только мы знаем длину сторон эквилатериального треугольника, можно вычислить координаты точки, заданной центральной точкой, радиус окружности, и горизонтальное основание.

для любого ленивого (как я) , кто просто хочет координаты для равностороннего треугольника на единичном круге:

A: (-0.866, -0.5)
B: (0.866, -0.5)
C: (0.0, 1.0)

для другой позиции и/или радиуса умножьте все значения на r, затем добавить cx до x координаты и cy до ys.

Это мои методы рисования треугольника на java (android):

mA = new PointD();
mB = new PointD();
mC = new PointD();
mCos120 = Math.cos(AppHelper.toRadians(120));
mSin120 = Math.sin(AppHelper.toRadians(120));
mCos240 = Math.cos(AppHelper.toRadians(240));
mSin240 = Math.sin(AppHelper.toRadians(240));

double r = 30; // this is distance from the center to one of triangle's point.
mA.set(0 + r, 0);
mB.x = mA.x * mCos120 - mA.y  * mSin120;
mB.y = mA.x * mSin120 + mA.y * mCos120;
mC.x = mA.x * mCos240 - mA.y * mSin240;
mC.y = mA.x * mSin240 + mA.y * mCos240;

mA = AppHelper.toScreenCoordinates(mCenterPoint, mA);
mB = AppHelper.toScreenCoordinates(mCenterPoint, mB);
mC = AppHelper.toScreenCoordinates(mCenterPoint, mC);

mPlayPath.reset();
mPlayPath.moveTo(mA.getX(), mA.getY());
mPlayPath.lineTo(mB.getX(), mB.getY());
mPlayPath.lineTo(mC.getX(), mC.getY());
mPlayPath.lineTo(mA.getX(), mA.getY());
mPlayPath.close();

public static PointD toScreenCoordinates(PointD center, PointD point) {
    return new PointD(point.x + center.x, center.y - point.y);
}

где PointD похож на PointF, но с двойным типом.