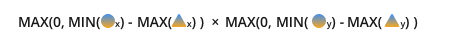Насколько пересекаются два прямоугольника?

формула для пересечения будут

SI= Max(0, Min(XA2, XB2) - Max(XA1, XB1)) * Max(0, Min(YA2, YB2) - Max(YA1, YB1))

тогда союз будет S=SA+SB-SI

и, наконец, соотношение будет SI / S.

предполагая два прямоугольника A и B, узнайте, насколько они перекрываются, и если да, верните размер области:

IF A.right < B.left OR A.left > B.right
    OR A.bottom < B.top OR A.top > B.bottom THEN RETURN 0

width := IF A.right > B.right THEN B.right - A.left ELSE A.right - B.left
height := IF A.bottom > B.bottom THEN B.bottom - A.top ELSE A.bottom - B.top

RETURN width * height

предполагая, что прямоугольник должен быть параллелен x и y axis, как это кажется, ситуация из предыдущих комментариев и ответов.

Я пока не могу опубликовать комментарий, но я хотел бы отметить, что оба предыдущих ответа, похоже, игнорируют случай, когда один боковой прямоугольник полностью находится в стороне от другого прямоугольника. Пожалуйста, поправьте меня, если я ошибаюсь.

рассмотрим случай

a: (1,1), (4,4)
b: (2,2), (5,3)

в этом случае мы видим, что для пересечение, высота должна быть bTop - bBottom потому что вертикальная часть b полностью содержится в a.

нам просто нужно добавить больше случаев следующим образом: (код может быть закорочен, если вы рассматриваете верх и низ как то же самое, что справа и слева, так что вам не нужно дублировать условный кусок дважды, но это должно сделать.)

if aRight <= bLeft or bRight <= aLeft or aTop <= bBottom or bTop <= aBottom:
    # There is no intersection in these cases
    return 0
else:
    # There is some intersection

    if aRight >= bRight and aLeft <= bLeft:
        # From x axis point of view, b is wholly contained in a
        width = bRight - bLeft
    elif bRight >= aRight and bLeft <= aLeft:
        # From x axis point of view, a is wholly contained in b
        width = aRight - aLeft
    elif aRight >= bRight:
        width = bRight - aLeft
    else:
        width = aRight - bLeft

    if aTop >= bTop and aBottom <= bBottom:
        # From y axis point of view, b is wholly contained in a
        height = bTop - bBottom
    elif bTop >= aTop and bBottom <= aBottom:
        # From y axis point of view, a is wholly contained in b
        height = aTop - aBottom
    elif aTop >= bTop:
        height = bTop - aBottom
    else:
        height = aTop - bBottom

return width * height

просто фиксируя предыдущие ответы так, чтобы соотношение было между 0 и 1 (используя Python):

    # (x1,y1) top-left coord, (x2,y2) bottom-right coord, (w,h) size
    A = {'x1': 0, 'y1': 0, 'x2': 99, 'y2': 99, 'w': 100, 'h': 100}
    B = {'x1': 0, 'y1': 0, 'x2': 49, 'y2': 49, 'w':  50, 'h':  50}

    # overlap between A and B
    SA = A['w']*A['h']
    SB = B['w']*B['h']
    SI = np.max([ 0, 1 + np.min([A['x2'],B['x2']]) - np.max([A['x1'],B['x1']]) ]) * np.max([ 0, 1 + np.min([A['y2'],B['y2']]) - np.max([A['y1'],B['y1']]) ])
    SU = SA + SB - SI
    overlap_AB = float(SI) / float(SU)
    print 'overlap between A and B: %f' % overlap_AB

    # overlap between A and A
    B = A
    SB = B['w']*B['h']
    SI = np.max([ 0, 1 + np.min([A['x2'],B['x2']]) - np.max([A['x1'],B['x1']]) ]) * np.max([ 0, 1 + np.min([A['y2'],B['y2']]) - np.max([A['y1'],B['y1']]) ])
    SU = SA + SB - SI
    overlap_AA = float(SI) / float(SU)
    print 'overlap between A and A: %f' % overlap_AA

выход будет:

    overlap between A and B: 0.250000
    overlap between A and A: 1.000000

[ymin_a, xmin_a, ymax_a, xmax_a] = list(bbox_a)
[ymin_b, xmin_b, ymax_b, xmax_b] = list(bbox_b)

x_intersection = min(xmax_a, xmax_b) - max(xmin_a, xmin_b) + 1
y_intersection = min(ymax_a, ymax_b) - max(ymin_a, ymin_b) + 1

if x_intersection <= 0 or y_intersection <= 0:
    return 0
else:
    return x_intersection * y_intersection

@User3025064 является правильным и является самым простым решением, однако исключительность должна быть проверена сначала для прямоугольников, которые не пересекаются, например, для прямоугольников A & B (в Visual Basic):

If A.Top =< B.Bottom or A.Bottom => B.Top or A.Right =< B.Left or A.Left => B.Right then
    Exit sub   'No intersection
else
    width = ABS(Min(XA2, XB2) - Max(XA1, XB1))
    height = ABS(Min(YA2, YB2) - Max(YA1, YB1))
    Area = width * height      'Total intersection area.
End if

ответ @user3025064 является правильным ответом. Принятый ответ непреднамеренно переворачивает внутренние вызовы MAX и MIN. Нам также не нужно сначала проверять, пересекаются ли они или нет, если мы используем представленную формулу MAX(0,x) в отличие от ABS(x). Если они не пересекаются, MAX (0,x) возвращает ноль, что делает область пересечения 0 (т. е. непересекающейся).

Я предлагаю, чтобы @Yves Daoust исправил свой ответ, потому что он является принятым, который появляется для всех, кто ищет эту проблему. Еще раз, вот правильная формула для пересечения:

SI = Max(0, Min(XA2, XB2) - Max(XA1, XB1)) * Max(0, Min(YA2, YB2) - Max(YA1, YB1))

остальное как обычно. Союз:

SU = SA + SB - SI

и соотношение:

SI/SU

хотя принятый ответ верен, я думаю, что стоит изучить этот ответ таким образом, чтобы сделать обоснование ответа совершенно очевидным. Это слишком распространенный алгоритм, чтобы иметь неполный (или, что еще хуже, спорный) ответ. Более того, бросив мимолетный взгляд на данную формулу, вы можете упустить красоту, расширяемость и принимаемые решения.

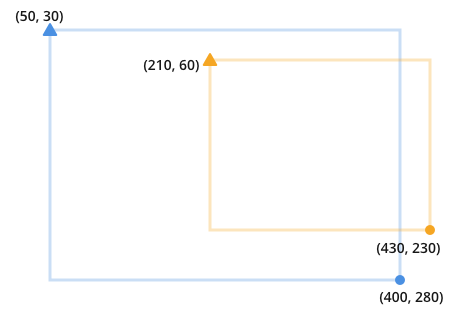
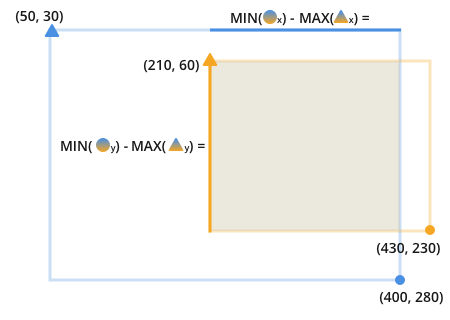
во-первых, рассмотрим один из способов определения двумерной коробка с:

• (x, y) для верхней левой точки
• (x, y) для нижней правой точки

Это может выглядеть так:

Я указываю на верхний левый треугольник и нижний правый круг. Это позволяет избежать непрозрачного синтаксиса, такого как x1, x2 для этого примера.

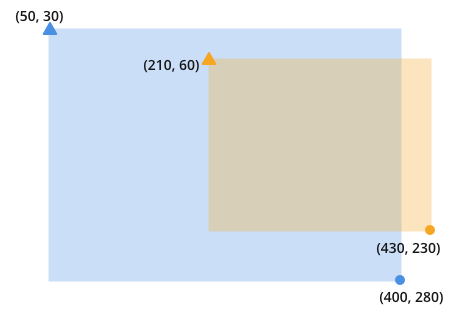
два перекрывающихся прямоугольника могут выглядеть так это:

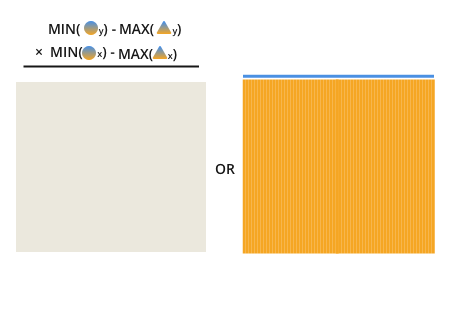
обратите внимание, что для поиска перекрытия вы ищете место, где оранжевый и синий сталкиваются:

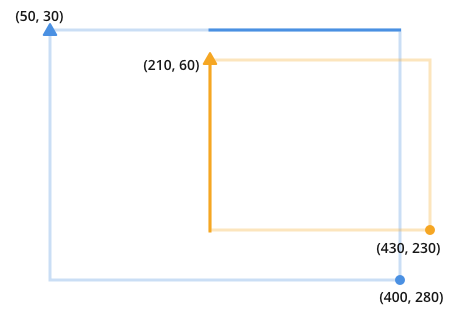
как только вы узнаете это, становится очевидным, что перекрытие является результатом нахождения и умножения этих двух затемненных линий:

длина каждой линии является минимальным значением точки окружности между линиями мы хотим сравнить, минус максимальное значение точек треугольника.

другими словами, длина линии, которая может поместиться на обе линии, которые мы сравниваем, производится путем вычитания ближайшей точки На самой длинной стороне линии из самой дальней точки На самой близкой стороне линии.

найти этих линий дает полную информацию о перекрывающихся областях.

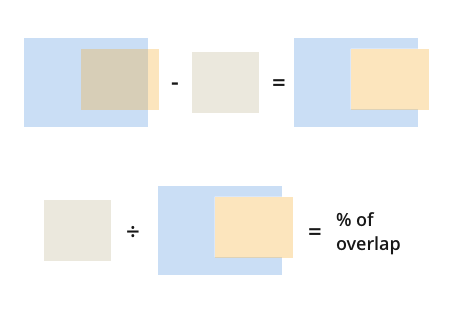
как только у вас есть это, найти процент перекрытия тривиально:

но подождите, если оранжевый прямоугольник не перекрывается с синим, то у вас будет проблема:

в этом примере, вы получаете -850 для наших перекрывающиеся области, что не может быть. Еще хуже, если обнаружение не перекрывается ни с тем, ни с другим размер (ни на оси x, ни на оси y), то вы все равно получите положительное число, потому что и размеры отрицательный. Вот почему вы видите Max(0, ...) * Max(0, ...) как часть решения; это гарантирует, что если какое-либо из перекрытий отрицательно, вы получите 0 от своей функции.

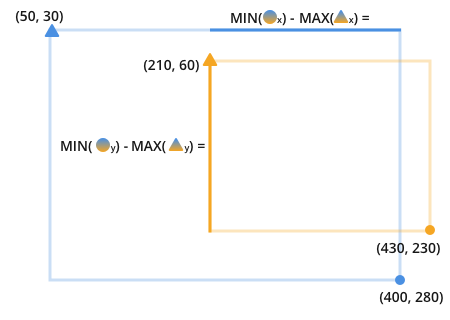
окончательная формула в соответствии с нашими символов:

стоит отметить, что с помощью max(0, ...) функция может быть не нужна. Вы можете хотите знать, если что-то перекрывается вдоль одного из его измерений, а не все из них; если вы используете max, вы уничтожите эту информацию. По этой причине, подумайте, как вы хотите иметь дело с непересекающимися образами. Обычно функция max подходит для использования, но стоит знать, что она делает.

наконец, обратите внимание, что, поскольку это сравнение касается только линейных измерений, его можно масштабировать до произвольных размеров или произвольных перекрывающихся четырехугольников.

подведем итоги:

intersecting_area = 
max(0, min(orange.circle.x, blue.circle.x) - max(orange.triangle.x, blue.triangle.x)) * max(0, min(orange.circle.y, blue_circle.y) - max(orange.triangle.y, blue.triangle.y))

percent_coverage = intersecting_area / (orange_area + blue_area - intersecting_area)