Найти пути между двумя заданными узлами?
скажем, у меня есть узлы, подключенные ниже, как я могу получить количество путей, которые существуют между заданными точками и деталями пути?
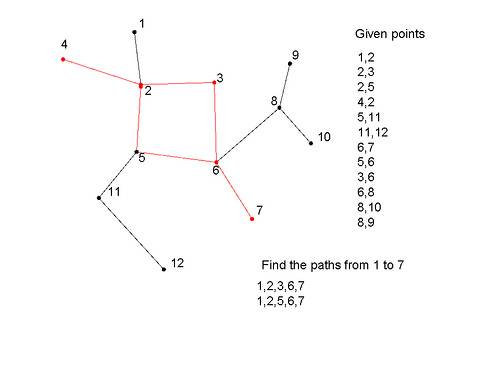
1,2 //node 1 and 2 are connected
2,3
2,5
4,2
5,11
11,12
6,7
5,6
3,6
6,8
8,10
8,9
найти пути от 1 до 7:
ответ: 2 пути найдены, и они
1,2,3,6,7
1,2,5,6,7
реализации здесь приятно, что я собираюсь использовать то же самое
вот фрагмент из приведенной выше ссылки в python
# a sample graph
graph = {'A': ['B', 'C','E'],
'B': ['A','C', 'D'],
'C': ['D'],
'D': ['C'],
'E': ['F','D'],
'F': ['C']}
class MyQUEUE: # just an implementation of a queue
def __init__(self):
self.holder = []
def enqueue(self,val):
self.holder.append(val)
def dequeue(self):
val = None
try:
val = self.holder[0]
if len(self.holder) == 1:
self.holder = []
else:
self.holder = self.holder[1:]
except:
pass
return val
def IsEmpty(self):
result = False
if len(self.holder) == 0:
result = True
return result
path_queue = MyQUEUE() # now we make a queue
def BFS(graph,start,end,q):
temp_path = [start]
q.enqueue(temp_path)
while q.IsEmpty() == False:
tmp_path = q.dequeue()
last_node = tmp_path[len(tmp_path)-1]
print tmp_path
if last_node == end:
print "VALID_PATH : ",tmp_path
for link_node in graph[last_node]:
if link_node not in tmp_path:
#new_path = []
new_path = tmp_path + [link_node]
q.enqueue(new_path)
BFS(graph,"A","D",path_queue)
-------------results-------------------
['A']
['A', 'B']
['A', 'C']
['A', 'E']
['A', 'B', 'C']
['A', 'B', 'D']
VALID_PATH : ['A', 'B', 'D']
['A', 'C', 'D']
VALID_PATH : ['A', 'C', 'D']
['A', 'E', 'F']
['A', 'E', 'D']
VALID_PATH : ['A', 'E', 'D']
['A', 'B', 'C', 'D']
VALID_PATH : ['A', 'B', 'C', 'D']
['A', 'E', 'F', 'C']
['A', 'E', 'F', 'C', 'D']
VALID_PATH : ['A', 'E', 'F', 'C', 'D']
8 ответов
поиск в ширину пересекает график и фактически находит все пути от начального узла. Однако обычно BFS не сохраняет все пути. Вместо этого он обновляет функцию prededecessor π, чтобы сохранить кратчайший путь. Вы можете легко изменить алгоритм так, что π(n) не только магазин один предшественник, но список возможных предшественников.
тогда все возможные пути кодируются в этой функции, и, пересекая π рекурсивно, вы получаете все возможные комбинации путей.
один хороший псевдокод, который использует эту запись можно найти в введение в алгоритмы по Кормена et al. и впоследствии использовался во многих университетских сценариях по этому вопросу. Поиск Google для "BFS псевдокода предшественника π" корней этот хит на Stack Exchange.
для тех, кто не является экспертом PYTHON, тот же код в C++
//@Author :Ritesh Kumar Gupta
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
vector<vector<int> >GRAPH(100);
inline void print_path(vector<int>path)
{
cout<<"[ ";
for(int i=0;i<path.size();++i)
{
cout<<path[i]<<" ";
}
cout<<"]"<<endl;
}
bool isadjacency_node_not_present_in_current_path(int node,vector<int>path)
{
for(int i=0;i<path.size();++i)
{
if(path[i]==node)
return false;
}
return true;
}
int findpaths(int source ,int target ,int totalnode,int totaledge )
{
vector<int>path;
path.push_back(source);
queue<vector<int> >q;
q.push(path);
while(!q.empty())
{
path=q.front();
q.pop();
int last_nodeof_path=path[path.size()-1];
if(last_nodeof_path==target)
{
cout<<"The Required path is:: ";
print_path(path);
}
else
{
print_path(path);
}
for(int i=0;i<GRAPH[last_nodeof_path].size();++i)
{
if(isadjacency_node_not_present_in_current_path(GRAPH[last_nodeof_path][i],path))
{
vector<int>new_path(path.begin(),path.end());
new_path.push_back(GRAPH[last_nodeof_path][i]);
q.push(new_path);
}
}
}
return 1;
}
int main()
{
//freopen("out.txt","w",stdout);
int T,N,M,u,v,source,target;
scanf("%d",&T);
while(T--)
{
printf("Enter Total Nodes & Total Edges\n");
scanf("%d%d",&N,&M);
for(int i=1;i<=M;++i)
{
scanf("%d%d",&u,&v);
GRAPH[u].push_back(v);
}
printf("(Source, target)\n");
scanf("%d%d",&source,&target);
findpaths(source,target,N,M);
}
//system("pause");
return 0;
}
/*
Input::
1
6 11
1 2
1 3
1 5
2 1
2 3
2 4
3 4
4 3
5 6
5 4
6 3
1 4
output:
[ 1 ]
[ 1 2 ]
[ 1 3 ]
[ 1 5 ]
[ 1 2 3 ]
The Required path is:: [ 1 2 4 ]
The Required path is:: [ 1 3 4 ]
[ 1 5 6 ]
The Required path is:: [ 1 5 4 ]
The Required path is:: [ 1 2 3 4 ]
[ 1 2 4 3 ]
[ 1 5 6 3 ]
[ 1 5 4 3 ]
The Required path is:: [ 1 5 6 3 4 ]
*/
алгоритм Дейкстры больше относится к взвешенным путям, и похоже, что плакат хотел найти все пути, а не только самые короткие.
для этого приложения я бы построил график (ваше приложение звучит так, как будто его не нужно направлять) и использовать ваш любимый метод поиска. Похоже, вы хотите все пути, а не только угадать самый короткий, поэтому используйте простой рекурсивный алгоритм по вашему выбору.
единственная проблема с этим, если график может быть циклический.
с подключения:
- 1, 2
- 1, 3
- 2, 3
- 2, 4
пока ищущ путь от 1 - >4, Вы смогли иметь цикл 1 -> 2 -> 3 -> 1.
в этом случае я бы сохранил стек как пересекающий узлы. Вот список с шагами для этого графика и полученного стека (извините за форматирование-нет опции таблицы):
текущего узла (возможные следующие узлы минус откуда мы пришли) [stack]
- 1 (2, 3) [1]
- 2 (3, 4) [1, 2]
- 3 (1) [1, 2, 3]
- 1 (2, 3) [1, 2, 3, 1] //ошибки - повторяющиеся числа в стек - цикл обнаружены
- 3 () [1, 2, 3] // отступил к третьему узлу и вытащил 1 из стопки. Нет больше узлов, чтобы исследовать от вот!--10-->
- 2 (4) [1, 2] // отступил к узлу 2 и вытащил 1 из стека.
- 4 () [1, 2, 4] // Target node found-стек записей для пути. Нет больше узлов, чтобы исследовать отсюда
- 2 () [1, 2] //отступил к узлу 2 и вытащил 4 из стека. Нет больше узлов, чтобы исследовать отсюда
- 1 (3) [1] //назад-шагнул к узлу 1 и выскочил 2 из стек.
- 3 (2) [1, 3]
- 2 (1, 4) [1, 3, 2]
- 1 (2, 3) [1, 3, 2, 1] //ошибки - повторяющиеся числа в стек - цикл обнаружены
- 2 (4) [1, 3, 2] //назад-шагнул к узлу 2 и выскочил 1 из стека
- 4 () [1, 3, 2, 4] Target node found-стек записей для пути. Нет больше узлов, чтобы исследовать от вот!--10-->
- 2 () [1, 3, 2] //отступил к узлу 2 и вытащил 4 из стека. Нет больше узлов
- 3 () [1, 3] // отступил к узлу 3 и вытащил 2 из стека. Нет больше узлов
- 1 () [1] // отступил к узлу 1 и вытащил 3 из стека. Нет больше узлов
- сделано с 2 записанными путями [1, 2, 4] и [1, 3, 2, 4]
исходный код немного громоздкий, и вы можете использовать коллекции.вместо этого deque, если вы хотите использовать BFS, чтобы найти, существует ли путь между 2 точками на графике. Вот быстрое решение, которое я взломал:
Примечание: этот метод может продолжаться бесконечно, если нет пути между двумя узлами. Я проверил не все случаи, ИММ.
from collections import deque
# a sample graph
graph = {'A': ['B', 'C','E'],
'B': ['A','C', 'D'],
'C': ['D'],
'D': ['C'],
'E': ['F','D'],
'F': ['C']}
def BFS(start, end):
""" Method to determine if a pair of vertices are connected using BFS
Args:
start, end: vertices for the traversal.
Returns:
[start, v1, v2, ... end]
"""
path = []
q = deque()
q.append(start)
while len(q):
tmp_vertex = q.popleft()
if tmp_vertex not in path:
path.append(tmp_vertex)
if tmp_vertex == end:
return path
for vertex in graph[tmp_vertex]:
if vertex not in path:
q.append(vertex)
в прологе (в частности, SWI-Prolog)
:- use_module(library(tabling)).
% path(+Graph,?Source,?Target,?Path)
:- table path/4.
path(_,N,N,[N]).
path(G,S,T,[S|Path]) :-
dif(S,T),
member(S-I, G), % directed graph
path(G,I,T,Path).
дана матрица смежности:
{0, 1, 3, 4, 0, 0}
{0, 0, 2, 1, 2, 0}
{0, 1, 0, 3, 0, 0}
{0, 1, 1, 0, 0, 1}
{0, 0, 0, 0, 0, 6}
{0, 1, 0, 1, 0, 0}
следующий код Wolfram Mathematica решает проблему поиска всех простых путей между двумя узлами графа. Я использовал простую рекурсию и два глобальных var для отслеживания циклов и хранения желаемого результата. код не был оптимизирован только для ясности кода. "печать" должна быть полезной, чтобы уточнить, как она работает.
cycleQ[l_]:=If[Length[DeleteDuplicates[l]] == Length[l], False, True];
getNode[matrix_, node_]:=Complement[Range[Length[matrix]],Flatten[Position[matrix[[node]], 0]]];
builtTree[node_, matrix_]:=Block[{nodes, posAndNodes, root, pos},
If[{node} != {} && node != endNode ,
root = node;
nodes = getNode[matrix, node];
(*Print["root:",root,"---nodes:",nodes];*)
AppendTo[lcycle, Flatten[{root, nodes}]];
If[cycleQ[lcycle] == True,
lcycle = Most[lcycle]; appendToTree[root, nodes];,
Print["paths: ", tree, "\n", "root:", root, "---nodes:",nodes];
appendToTree[root, nodes];
];
];
appendToTree[root_, nodes_] := Block[{pos, toAdd},
pos = Flatten[Position[tree[[All, -1]], root]];
For[i = 1, i <= Length[pos], i++,
toAdd = Flatten[Thread[{tree[[pos[[i]]]], {#}}]] & /@ nodes;
(* check cycles!*)
If[cycleQ[#] != True, AppendTo[tree, #]] & /@ toAdd;
];
tree = Delete[tree, {#} & /@ pos];
builtTree[#, matrix] & /@ Union[tree[[All, -1]]];
];
];
для вызова кода: initNode = 1; endNode = 6; lcycle = {}; дерево = {{initNode}}; builtTree[initNode, matrix];
пути: {{1}} корень: 1 - - - узлы: {2,3,4}
пути: {{1,2},{1,3},{1,4}} корень: 2 - - - узлы: {3,4,5}
пути: {{1,3},{1,4},{1,2,3},{1,2,4},{1,2,5}} корень: 3 - - - узлы: {2,4}
пути: {{1,4},{1,2,4},{1,2,5},{1,3,4},{1,2,3,4},{1,3,2,4},{1,3,2,5}} корень: 4 - - - узлы: {2,3,6}
пути: {{1,2,5},{1,3,2,5},{1,4,6},{1,2,4,6},{1,3,4,6},{1,2,3,4,6},{1,3,2,4,6},{1,4,2,5},{1,3,4,2,5},{1,4,3,2,5}} корень: 5 - - - узлы: {6}
результаты:{{1, 4, 6}, {1, 2, 4, 6}, {1, 2, 5, 6}, {1, 3, 4, 6}, {1, 2, 3, 4, 6}, {1, 3, 2, 4, 6}, {1, 3, 2, 5, 6}, {1, 4, 2, 5, 6}, {1, 3, 4, 2, 5, 6}, {1, 4, 3, 2, 5, 6}}
...К сожалению, я не могу загрузить изображения, чтобы показать результаты в лучшем случае : (
Если вы хотите все пути, используйте рекурсию.
используя список смежности, желательно создать функцию f (), которая пытается заполнить текущий список посещенных вершин. Вот так:
void allPaths(vector<int> previous, int current, int destination)
{
previous.push_back(current);
if (current == destination)
//output all elements of previous, and return
for (int i = 0; i < neighbors[current].size(); i++)
allPaths(previous, neighbors[current][i], destination);
}
int main()
{
//...input
allPaths(vector<int>(), start, end);
}
из-за того, что вектор передается по значению (и, следовательно, любые изменения, внесенные в рекурсивной процедуры не постоянный), все возможные комбинации перечисленных.
вы можете получить немного эффективности, передав вектор по ссылке (и, следовательно, не нужно копировать вектор снова и снова), но вам нужно будет убедиться, что все будет popped_back () вручную.
еще одна вещь: если график имеет циклы, это не будет работать. (Я предполагаю, что в этом случае вы захотите найти все простой пути, затем), прежде чем добавить что-то в вектор, сначала проверьте, если он уже там.
Если вы хотите, чтобы все короткий пути, используйте Конрада предложение с этим алгоритмом.
то, что вы пытаетесь сделать, по существу, найти путь между двумя вершинами в (направленном?) график проверить алгоритм Дейкстры Если вам нужен кратчайший путь или напишите простую рекурсивную функцию, если вам нужны любые пути.
