найти точку пересечения двух линий, нарисованных с помощью houghlines opencv

вы не хотите получать пересечения параллельных линий; только пересечения вертикальных линий с горизонтальными линиями. Кроме того, поскольку у вас есть вертикальные линии, вычисление наклона, скорее всего, приведет к взрыву или INF-склонам, поэтому вы не должны использовать y = mx+b уравнения. Вам нужно сделать две вещи:

1. сегментируйте свои линии на два класса на основе их угла.
2. вычислить пересечения каждой линии в одном классе с строки в других классах.

С HoughLines, у вас уже есть результат как rho, theta таким образом, вы можете легко сегментировать на два класса угла с theta. Вы можете использовать, например,cv2.kmeans() С theta как ваши данные, которые вы хотите разделить.

затем, чтобы вычислить пересечения, вы можете использовать формулу для вычисление пересечений с учетом двух точек от каждой строки. Вы уже вычисляете две точки из каждой строки:(x1, y1), (x2, y2) так что вы можете просто храните их и используйте. Edit: на самом деле, как показано ниже в моем коде, есть формула, которую вы можете использовать для вычисления пересечений строк с rho, theta форма HoughLines дает.

я ответил:аналогичный вопрос раньше с некоторым кодом python, который вы можете проверить; обратите внимание, что это использовало HoughLinesP что дает вам только линейные сегменты.

пример кода

вы не предоставили свое исходное изображение, поэтому я не могу использовать это. Вместо этого я буду использовать стандартное изображение судоку, используемое OpenCV в своих учебниках преобразования и порога Hough:

во-первых, мы просто прочитали этот изображения и преобразование его с помощью адаптивной пороговой обработки, как то, что используется в этот учебник OpenCV:

import cv2
import numpy as np

img = cv2.imread('sudoku.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
blur = cv2.medianBlur(gray, 5)
adapt_type = cv2.ADAPTIVE_THRESH_GAUSSIAN_C
thresh_type = cv2.THRESH_BINARY_INV
bin_img = cv2.adaptiveThreshold(blur, 255, adapt_type, thresh_type, 11, 2)

тогда мы найдем линии Хоу с cv2.HoughLines():

rho, theta, thresh = 2, np.pi/180, 400
lines = cv2.HoughLines(bin_img, rho, theta, thresh)

теперь, если мы хотим найти пересечения, на самом деле мы хотим найти пересечения только перпендикулярных линий. Нам не нужны пересечения в основном параллельных линий. Поэтому нам нужно разделить наши линии. В этом конкретном примере вы можете легко проверить, является ли линия горизонтальной или вертикальной на основе простого теста; вертикальные линии будут иметь theta около 0 или около 180; горизонтальное линии будут иметь theta около 90. Однако, если вы хотите сегментировать их на основе произвольного количества углов, автоматически, без определения этих углов, я думаю, что лучшая идея-использовать cv2.kmeans().

есть одна хитрая вещь, чтобы получить права. HoughLines возвращает строки rho, theta форма (Гессе нормальная форма), и theta возвращено между 0 и 180 градусами, и линии вокруг 180 и 0 градусов подобны (они оба близки к горизонтальным линиям), поэтому нам нужен какой-то способ получить эту периодичность в kmeans.

если мы построим угол на единичном круге, но умножим угол на два, тогда углы первоначально вокруг 180 градусов станут близкими к 360 градусам и, таким образом, будут иметь x, y значения на единичной окружности почти одинаковы для углов при 0. Таким образом, мы можем получить некоторую приятную "близость" здесь, построив 2*angle с координатами на единичной окружности. Тогда мы можем бежать cv2.kmeans() по этим пунктам и сегменту автоматически с тем, сколько штук мы хотим.

Итак, давайте построим функцию для сегментации:

from collections import defaultdict
def segment_by_angle_kmeans(lines, k=2, **kwargs):
    """Groups lines based on angle with k-means.

    Uses k-means on the coordinates of the angle on the unit circle 
    to segment `k` angles inside `lines`.
    """

    # Define criteria = (type, max_iter, epsilon)
    default_criteria_type = cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER
    criteria = kwargs.get('criteria', (default_criteria_type, 10, 1.0))
    flags = kwargs.get('flags', cv2.KMEANS_RANDOM_CENTERS)
    attempts = kwargs.get('attempts', 10)

    # returns angles in [0, pi] in radians
    angles = np.array([line[0][1] for line in lines])
    # multiply the angles by two and find coordinates of that angle
    pts = np.array([[np.cos(2*angle), np.sin(2*angle)]
                    for angle in angles], dtype=np.float32)

    # run kmeans on the coords
    labels, centers = cv2.kmeans(pts, k, None, criteria, attempts, flags)[1:]
    labels = labels.reshape(-1)  # transpose to row vec

    # segment lines based on their kmeans label
    segmented = defaultdict(list)
    for i, line in zip(range(len(lines)), lines):
        segmented[labels[i]].append(line)
    segmented = list(segmented.values())
    return segmented

теперь использовать его, мы можем просто звоните:

segmented = segment_by_angle_kmeans(lines)

что приятно здесь мы можем указать произвольное количество групп, указав необязательный аргумент k (по умолчанию k = 2 поэтому я не указал его здесь).

если мы построим линии из каждой группы с другим цвет:

и теперь все, что осталось, это найти пересечения каждой линии в первой группе с пересечением каждой линии во второй группе. Поскольку линии находятся в нормальной форме Гессена, существует хорошая формула линейной алгебры для вычисления пересечения линий из этой формы. См.здесь. Давайте создадим здесь две функции: одну, которая находит пересечение только двух линий, и одну функцию, которая петляет через все строки в группах и использует эту более простую функцию для двух строк:

def intersection(line1, line2):
    """Finds the intersection of two lines given in Hesse normal form.

    Returns closest integer pixel locations.
    See https://stackoverflow.com/a/383527/5087436
    """
    rho1, theta1 = line1[0]
    rho2, theta2 = line2[0]
    A = np.array([
        [np.cos(theta1), np.sin(theta1)],
        [np.cos(theta2), np.sin(theta2)]
    ])
    b = np.array([[rho1], [rho2]])
    x0, y0 = np.linalg.solve(A, b)
    x0, y0 = int(np.round(x0)), int(np.round(y0))
    return [[x0, y0]]


def segmented_intersections(lines):
    """Finds the intersections between groups of lines."""

    intersections = []
    for i, group in enumerate(lines[:-1]):
        for next_group in lines[i+1:]:
            for line1 in group:
                for line2 in next_group:
                    intersections.append(intersection(line1, line2)) 

    return intersections

тогда, чтобы использовать его, это просто:

intersections = segmented_intersections(segmented)

и, построив все перекрестки, получаем:

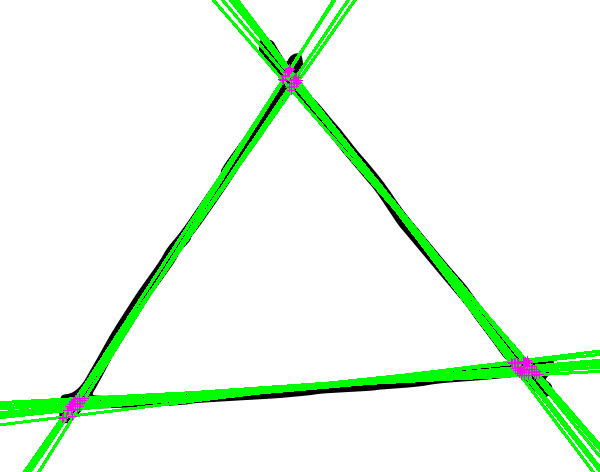
как упоминалось выше, этот код может сегментировать линии более чем на две группы углов. Вот он работает на рисованном треугольнике и вычисляет точки пересечения обнаруженных линий с помощью k=3: