Нелинейная регрессия e^(-x) с использованием scipy, python, numpy
приведенный ниже код дает мне плоскую линию для линии наилучшего соответствия, а не хорошую кривую вдоль модели e^(-x), которая будет соответствовать данным. Может ли кто-нибудь показать мне, как исправить код ниже, чтобы он соответствовал моим данным?
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize
def _eNegX_(p,x):
x0,y0,c,k=p
y = (c * np.exp(-k*(x-x0))) + y0
return y
def _eNegX_residuals(p,x,y):
return y - _eNegX_(p,x)
def Get_eNegX_Coefficients(x,y):
print 'x is: ',x
print 'y is: ',y
# Calculate p_guess for the vectors x,y. Note that p_guess is the
# starting estimate for the minimization.
p_guess=(np.median(x),np.min(y),np.max(y),.01)
# Calls the leastsq() function, which calls the residuals function with an initial
# guess for the parameters and with the x and y vectors. Note that the residuals
# function also calls the _eNegX_ function. This will return the parameters p that
# minimize the least squares error of the _eNegX_ function with respect to the original
# x and y coordinate vectors that are sent to it.
p, cov, infodict, mesg, ier = scipy.optimize.leastsq(
_eNegX_residuals,p_guess,args=(x,y),full_output=1,warning=True)
# Define the optimal values for each element of p that were returned by the leastsq() function.
x0,y0,c,k=p
print('''Reference data:
x0 = {x0}
y0 = {y0}
c = {c}
k = {k}
'''.format(x0=x0,y0=y0,c=c,k=k))
print 'x.min() is: ',x.min()
print 'x.max() is: ',x.max()
# Create a numpy array of x-values
numPoints = np.floor((x.max()-x.min())*100)
xp = np.linspace(x.min(), x.max(), numPoints)
print 'numPoints is: ',numPoints
print 'xp is: ',xp
print 'p is: ',p
pxp=_eNegX_(p,xp)
print 'pxp is: ',pxp
# Plot the results
plt.plot(x, y, '>', xp, pxp, 'g-')
plt.xlabel('BPM%Rest')
plt.ylabel('LVET/BPM',rotation='vertical')
plt.xlim(0,3)
plt.ylim(0,4)
plt.grid(True)
plt.show()
return p
# Declare raw data for use in creating regression equation
x = np.array([1,1.425,1.736,2.178,2.518],dtype='float')
y = np.array([3.489,2.256,1.640,1.043,0.853],dtype='float')
p=Get_eNegX_Coefficients(x,y)
1 ответов
похоже, что это проблема с вашими первоначальными догадками; что-то вроде (1, 1, 1, 1) отлично работает: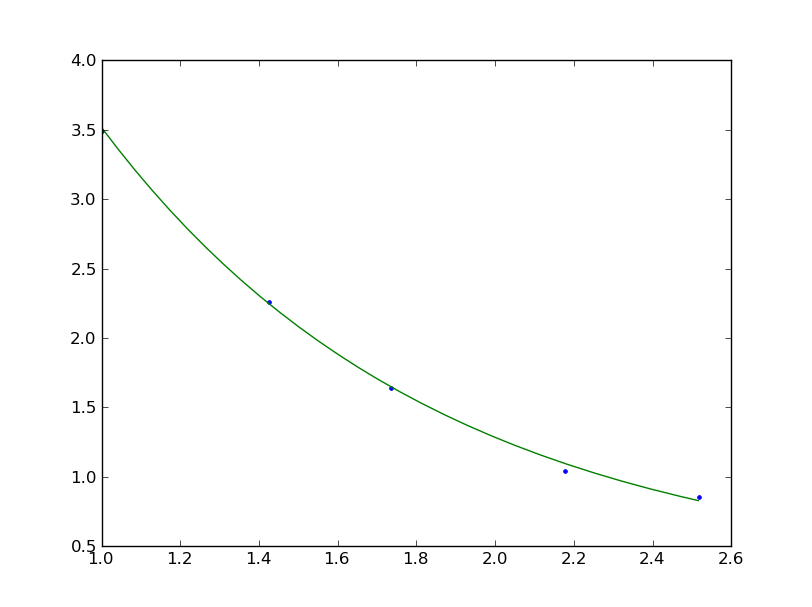
У вас есть
p_guess=(np.median(x),np.min(y),np.max(y),.01)
функции
def _eNegX_(p,x):
x0,y0,c,k=p
y = (c * np.exp(-k*(x-x0))) + y0
return y
так это test_data_maxe^ ( -.01(x - test_data_median)) + test_data_min
Я не знаю много об искусстве выбора хороших стартовых параметров, но я могу сказать несколько вещей. leastsq находит локальный минимум здесь-ключ в выборе этих значений-найти правильная гора, чтобы подняться, а не пытаться сократить работу, которую должен делать алгоритм минимизации. Ваша первоначальная догадка выглядит так (green):
(1.736, 0.85299999999999998, 3.4889999999999999, 0.01)
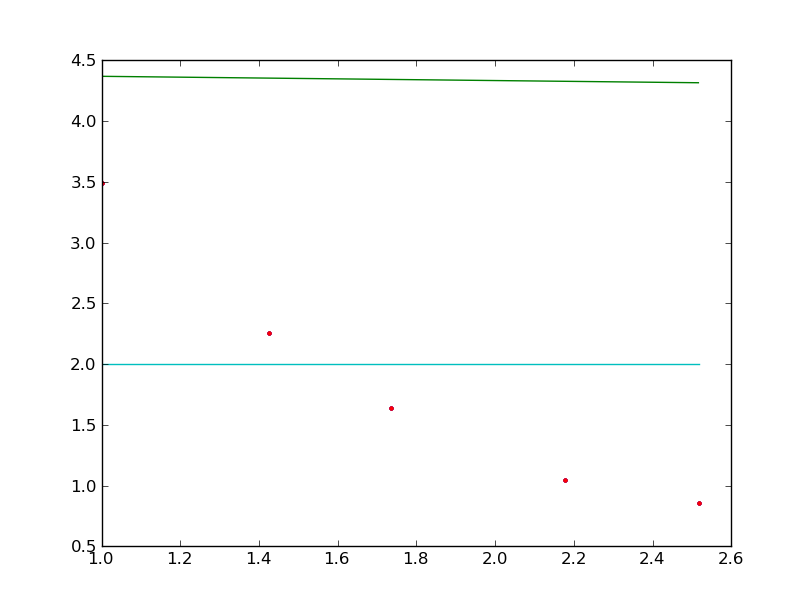
что приводит к вашей плоской линии (синий):
(-59.20295956, 1.8562 , 1.03477144, 0.69483784)
больший прирост был достигнут при регулировке высоты линии, чем при увеличении значения k. Если вы знаете, что подходите к такого рода данным, используйте больший k. Если вы не знаете, я думаю, вы можете попытаться найти достойное значение k, взяв пробу данные или работа со склона между средней частью первой половины и второй половиной, но я не знаю, как это сделать.
Edit: вы также можете начать с нескольких догадок, выполнить минимизацию несколько раз и взять строку с самыми низкими остатками.
