Нормальный вектор трех точек
Эй, математические выродки, у меня есть проблема, которая ставила меня в тупик некоторое время. Это для личного проекта.
У меня три точки: красная, зеленая и синяя. Они расположены на картонной карточке так, что красная точка находится в левом нижнем углу (0,0), синяя точка-в правом нижнем углу (1,0), а зеленая точка-в левом верхнем углу. Представьте, что вы отступаете назад и фотографируете карту под углом. Если вы должны были найти центр каждой точки На картинке (скажем, единицы пиксели), как бы вы нашли нормальный вектор лица карты на картинке (относительно камеры)?
теперь несколько вещей, которые я подобрал об этой проблеме:
- точки (в реальной жизни) всегда под прямым углом. На картинке они только под прямым углом, если камера была повернута вокруг красной точки вдоль " оси " (ось-линия, созданная красными и синими или красными и зелеными точками).
- есть точки только на одной стороне карта. Таким образом, вы знаете, вы никогда не будете смотреть на это.
- расстояние карты до камеры не имеет значения. Если бы я знал глубину каждой точки, это было бы намного проще (просто простое перекрестное произведение, нет?).
- вращение карты не имеет никакого отношения к тому, что я ищу. В том, что я делал, чтобы попытаться понять это, вращение можно найти с помощью нормального вектора в конце. Будет ли вращение часть (или произведение) нахождения нормального вектора мне неизвестна.
надеюсь, что есть кто-то, кто либо сделал это, либо является математическим гением. Двое моих друзей помогают мне в этом, и до сих пор нам это не удавалось.
6 ответов
Я разработал его в своей старой версии MathCAD:
alt текст http://i47.tinypic.com/4fjhs.jpg
Edit: неверная формулировка на скриншоте MathCAD: "Known:g и b are перпендикулярно друг с другом"
в MathCAD я забыл последний шаг выполнения кросс-продукта, который я скопирую здесь из моего предыдущего ответа:
теперь мы решили для X-Y-Z переведенные точки g и b, ваши оригинальный вопрос хотел нормальный самолет.
Если крест g x b, мы получим вектор нормальный для обоих:
| u1 u2 u3 | g x b = | g1 g2 g3 | | b1 b2 b3 | = (g2b3 - b2g3)u1 + (b1g3 - b3g1)u2 + (g1b2 - b1g2)u3все значения известны, подключите их (я не буду писать версию с g3 и В3 заменить, так как это просто слишком длинный и уродливый, чтобы быть полезным.
но на практике, я думаю, вам придется решить его численно, регулируя gz и bz чтобы наилучшим образом соответствовать условиям:
g · b = 0
и
|g/=/b|
поскольку пиксели не являются алгебраически совершенными.
пример
используя изображение астронавтов Apollo 13, оснащающих один из квадратов командного модуля Канистра с гидроксидом лития для работы в Лэм, я расположил углы:
alt текст http://i48.tinypic.com/2heahit.jpg
используя их в качестве основы для плоскости X-Y:
alt текст http://i47.tinypic.com/wj9zsx.jpg
Я записал местоположения пикселей с помощью Photoshop, с положительным X справа и положительным Y вниз (чтобы сохранить правое правило Z"на" картинка):
g = (79.5, -48.5, gz)
b = (-110.8, -62.8, bz)
пробивание двух начальных формул в Excel и использование пакета инструментов анализа для"свернуть " ошибка при регулировке gz и bz, он придумал два значения Z:
g = (79.5, -48.5, 102.5)
b = (-110.8, -62.8, 56.2)
что позволяет мне вычислить другие интересные значения.
длина g и b в пикселях:
|g| = 138.5
|b| = 139.2
вектор нормали:
g x b = (3710, -15827, -10366)
единица нормальные (длина 1):
uN = (0.1925, -0.8209, -0.5377)
масштабирование нормально до той же длины (в пикселях), что и g и b (138.9):
нормальный = (26.7, -114.0, -74.7)
теперь, когда у меня есть нормальный, который имеет ту же длину, что и g и b, я нарисовал их на той же картинке:
alt-текст http://i47.tinypic.com/2qjzp0i.jpg
Я думаю, у вас будет новая проблема: искажение, введенное объективом камеры. Три точки не идеально проецируются на 2-мерную фотографическую плоскость. Существует сферическое искажение, которое делает прямые линии более не прямыми, делает равные длины более не равными и делает нормали немного отклоненными от нормы.
Microsoft research имеет алгоритм, чтобы выяснить, как исправить для камеры искажение:
гибкий новый метод для калибровки камеры
но это выше моего понимания:
мы предлагаем гибкий новый метод к легко откалибруйте камеру. Это хорошо подходит для использования без специализированных знание 3D геометрии или компьютер видение. Техника только требует камера для наблюдения за плоским рисунком показано на нескольких (не менее двух) разные ориентации. Либо камера или плоскостная картина могут быть свободно перемещаться. Движение не должно быть известный. Радиальное искажение объектива моделированный. Предлагаемая процедура состоит из решения закрытой формы, с последующим нелинейным уточнением на основе максимального правдоподобия критерий. Оба компьютерного моделирования и реальные данные были использованы для проверки предлагаемая техника и очень хорошая получены результаты. Сравнимый с классическими методами, которые используют дорогие оборудования как 2 или три ортогональные плоскости, предлагаемые техника проста в использовании и гибкий. Он продвигает 3D компьютерных видения один шаг от лабораторных условий к реальное использование.
у них есть образец изображения, где можно увидеть искажение:

Примечание
- вы не знаете, видите ли вы "верхнюю" часть картона или "нижнюю", поэтому Нормаль может быть отражена вертикально (т. е. z = - z)
обновление
Гай нашел ошибку в производных алгебраических формулах. Исправление этого приводит к формулам, которые я, не думаю, имеют простую закрытую форму. Это не так уж плохо, так как его все равно нельзя решить точно; но численно.
вот скриншот из Excel, где я начинаю с двух правил knowns:
g · b = 0
и
|g/=/b|
запись 2-го в качестве разницы (сумма" ошибка"), вы можете добавить оба и использовать это значение в качестве числа, чтобы иметь решатель excel свернуть:
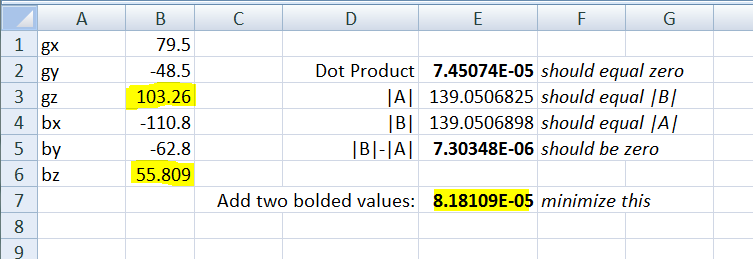
Это означает, что вам придется написать свой собственный числовой итерационный решатель. я смотрю на свой численные методы для инженеров учебник из университета; я знаю, что он содержит алгоритмы для решения рекурсивных уравнения без простой замкнутой формы.
из его звуков, у вас есть три точки p1, p2 и p3 определение плоскости, и вы хотите, чтобы найти нормальный вектор к плоскости.
представление точек в виде векторов от начала координат, an уравнение нормального вектора будет
n = (p2 - p1) x (p3 - p1)
(где x-перекрестное произведение двух векторов)
Если вы хотите, чтобы вектор указывал наружу от перед карты, затем Ала правое правило, установить
p1 = красная точка
p2 = синяя (внизу справа) точка
p3 = зеленый (вверху слева) точка
@ Ian Boyd...Мне понравилось ваше объяснение, только я застрял на Шаге 2, Когда вы сказали, чтобы решить для bz. У тебя все еще было bz в вашем ответе, и я не думаю, что вы должны есть!--1-->bz в вашем ответе...
bz должно быть +/- квадратный корень gx2 + gy2 + gz2 - bx2 - by2
после того, как я сделал это сам, мне было очень трудно заменить bz в первое уравнение, когда вы решили для гz, потому что при замене bz, сейчас вы получите:
gz = - (gxbx + gyby) / sqrt (gx2 + gy2 + gz2 - bx2 - by2 )
часть, которая затрудняет это, заключается в том, что есть gz в квадратном корне, поэтому вы должны отделить его и объединить gz вместе, и решить для gz что я и сделал, только я не думаю, что мой способ решения был правильным, потому что, когда я написал свою программу для расчета gz для меня, я использовал свой gx и gy значения, чтобы увидеть, соответствует ли мой ответ вашему, и это не так.
так что я подумал, не могли бы вы мне помочь, потому что мне действительно нужно, чтобы это сработало для одного из моих проектов. Спасибо!
просто думаю на ногах здесь.
ваши эффективные входы-это кажущееся соотношение RB / RG [+], кажущийся угол BRG и угол, который (скажем) RB делает с вашей координатной осью Y экрана (я что-то пропустил). Вам нужны компоненты нормализованного нормального (heh!) вектор, который я считаю только двумя независимыми значениями (хотя у вас остается двусмысленность спереди-сзади, если карта просматривается).[++]
поэтому я предполагаю, что это вероятный...
отсюда я работаю над предположением, что кажущийся угол RB всегда равен 0, и мы можем повернуть окончательное решение вокруг оси z позже.
начните с карты, расположенной параллельно плоскости просмотра и ориентированной "естественным" способом (т. е. вы верхний против Нижнего и левого против правого назначений уважаются). Мы можем достичь всех интересных позиций карты, вращаясь на \theta вокруг начальной оси x (для -\pi/2 < \theta < \pi/2), а затем поворачивать на \phi вокруг начальной оси y (для -\pi/2 < \phi < \pi/2). Заметим, что мы сохранили видимое направление вектора RB.
следующий шаг вычислить кажущееся отношение и кажущийся угол после в терминах \theta и \phi и инвертирует результат.[+++]
нормальным будет R_y(\phi)R_x(\theta)(0, 0, 1) на R_i примитивная матрица вращения вокруг оси i.
[+] абсолютные длины не учитываются, потому что это просто говорит вам расстояние до карты.
[++] Еще одно предположение: расстояние от карты до плоскости просмотра намного больше, чем размер карты.
[++ + ] здесь важна проекция, которую вы используете от трехмерного пространства до плоскости просмотра. Это трудная часть, но не то, что мы можем сделать для вас, если вы не скажете, какую проекцию вы используете. Если вы используете реальную камеру, то это перспективная проекция и освещается практически в любой книге по 3D-графике.
правильный, нормальный вектор не изменяется по расстоянию, но проекция картона на картинке тут изменение по расстоянию (просто: если у вас есть небольшой картон, ничего не меняется. Если у вас есть картон шириной в 1 милю и высотой в 1 милю, и вы поворачиваете его так, чтобы одна сторона была ближе, а другая-дальше, ближняя сторона увеличивается, а дальняя сторона сокращается на картинке. Вы можете сразу увидеть, что прямоугольник не остается прямоугольником, а трапеция)
наиболее точный способ для малых углов и камеры, центрированной на середине, - измерить соотношение ширины / высоты между "нормальным" изображением и угловым изображением на средних линиях (потому что они не деформированы).
мы определяем x как слева направо, y как вниз до вверх, z как далеко до Ближнего.
затем
x = arcsin (measuredWidth/normWidth) красно-синий
y = arcsin (measuredHeight/normHeight) красно-зеленый
Зет= sqrt (1.0-x^2-y^2)
я рассчитаю завтра более точное решение, но сейчас я слишком устал...
вы можете использовать u,v, n co-oridnates. Установите точку обзора в положение "глаза" или "камеры", затем переведите координаты x,y,z в u,v,n. Оттуда вы можете определить нормали,а также перспективные и видимые поверхности,если хотите (u', v', n'). Кроме того, имейте в виду, что 2D = 3D с z=0. Наконец, убедитесь, что вы используете однородные координаты.
