Nullability (Регулярные Выражения)

в "производных регулярных выражений" Бжозовского и в других местах функция δ (R), возвращающая λ, если R обнуляется, и ∅ в противном случае включает такие предложения, как:

δ(R1 + R2) = δ(R1) + δ(R2)
δ(R1 · R2) = δ(R1) ∧ δ(R2)

понятно, что если оба R1 и R2 значение null тогда (R1 * R2) является недействительным, и если либо R1 или R2 может принимать значение null тогда (R1 + R2) иметь значение null. Мне непонятно, что предполагают вышеуказанные пункты в смысле, однако. Моя первая мысль, отображение ( + ), ( · ) или булевых операций в регулярные множества бессмысленно, так как в базовом случае

δ(a) = ∅ (for all a ∈ Σ)
δ(λ) = λ
δ(∅) = ∅

и λ не является множеством (и не является множеством возвращаемого типа δ, который является регулярным выражением). Кроме того, это отображение не указано, и для него есть отдельная нотация. Я понимаю ничтожность, но я теряюсь в определении суммы, произведения и булевых операций в определении δ: как λ или ∅ возвращаются из δ(R1) δ δ (R2), например, в определении off δ (R1 * R2)?

6
derivative nullable regex

3 ответов

Я думаю, что вы попадаетесь на нотационных вольностях, принятых автором. Возвращаемый тип δ (R), безусловно, является множеством или, скорее, языком. Если вы посмотрите на определение:

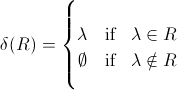
alt text

вы можете видеть, что существует несоответствие в возвращаемом типе, формально λ является элементом, но ∅ является пустым языком... Что он должен сказать:

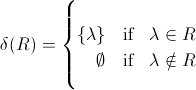
alt text

тот факт, что автор использует λ как для пустой строки, так и для язык, содержащий только пустую строку, дополнительно подтверждается его определением оператора Kleene star:

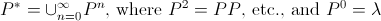
alt text

ясно, что последняя часть должна быть 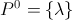alt text если мы хотим быть педантичным.

учитывая, что возвращаемый тип δ(R) является множеством или, скорее, языком, уравнения, которые вы даете, имеют смысл и выражают именно то, что вы описали.

2

я думаю, вы были правы карте + и ^ в boolean or и and соответственно. Похоже, две строки, которые вы процитировали, имеют дело с чередование (сумма) и объединение (продукта):

δ(R1 + R2) = δ(R1) + δ(R2)

на чередование of R1 и R2 аннулируется, если R1 допускает R2аннулируется, или оба R1 и R2 допускают.

δ(R1 · R2) = δ(R1) ∧ δ(R2)

на объединение of R1 и R2 только аннулируется, если оба R1 и R2 допускают.

посмотреть здесь для реализации Haskell этих правил.

3

(Я не могу заглянуть в статью Бжозовского, чтобы лучше понять, что там подразумевается), но я могу предложить 2 способа интерпретировать эту нотацию (кроме gettingalong с нотацией, я вижу, нет никаких сомнений: предполагаемый смысл этого определения хорошо понят):

1) слева от определения у нас есть только "синтаксические" шаблоны для регулярных выражений. Справа, мы производим наборы; помните, что регулярное выражение-это способ обозначения языка (набор), и поэтому этот способ записать определение становится понятным: справа мы просто используем некоторые (простые) регулярные выражения в качестве короткого способа ссылки на наборы. То есть, означает пустой язык (пустое множество) и λ (если понял как регулярное выражение) означает язык, содержащий только пустое слово (набор с этим элементом).

операции-это просто операции над множествами: вероятно, объединение и пересечение.

Если нотация интерпретируемый таким образом, нет никакого противоречия с используемой нотацией, чтобы бросить вызов базовому случаю: опять же, "a" - это регулярное выражение, которое означает язык со словом "a".

2) Мы строим обычного expressons справа, в первую очередь, но автор расширил операций, построения регулярных выражений с клином, который имеет семантику пересечения языков.

2