NumPy PolyFit и PolyVal в нескольких измерениях?

предположим, что n-мерный массив наблюдений, которые преобразуются в 2d-массив с каждой строкой, являющейся одним набором наблюдений. Используя этот подход reshape,np.polyfit можно вычислить коэффициенты соответствия 2-го порядка для всего ndarray (векторизованного):

fit = np.polynomial.polynomialpolyfit(X, Y, 2)

где Y-форма (304000, 21), а X-вектор. Это приводит к массиву (304000,3) коэффициентов, fit.

используя итератор можно назвать np.polyval(fit, X) для каждой строки. Это неэффективно, когда векторизованный подход может существовать. Мог ли fit результат будет применен ко всему массиву наблюдений без итерации? Если да, то как?

это по линии это так вопрос.

6
arrays numpy python scipy

2 ответов

np.polynomial.polynomial.polyval принимает многомерные массивы коэффициент:

>>> x = np.random.rand(100)
>>> y = np.random.rand(100, 25)
>>> fit = np.polynomial.polynomial.polyfit(x, y, 2)
>>> fit.shape # 25 columns of 3 polynomial coefficients
(3L, 25L)
>>> xx = np.random.rand(50)
>>> interpol = np.polynomial.polynomial.polyval(xx, fit)
>>> interpol.shape # 25 rows, each with 50 evaluations of the polynomial
(25L, 50L)

и конечно же:

>>> np.all([np.allclose(np.polynomial.polynomial.polyval(xx, fit[:, j]),
...                     interpol[j]) for j in range(25)])
True
7

np.polynomial.polynomial.polyval - это прекрасный (и удобный) подход к эффективной оценке полиномиальных фитингов.

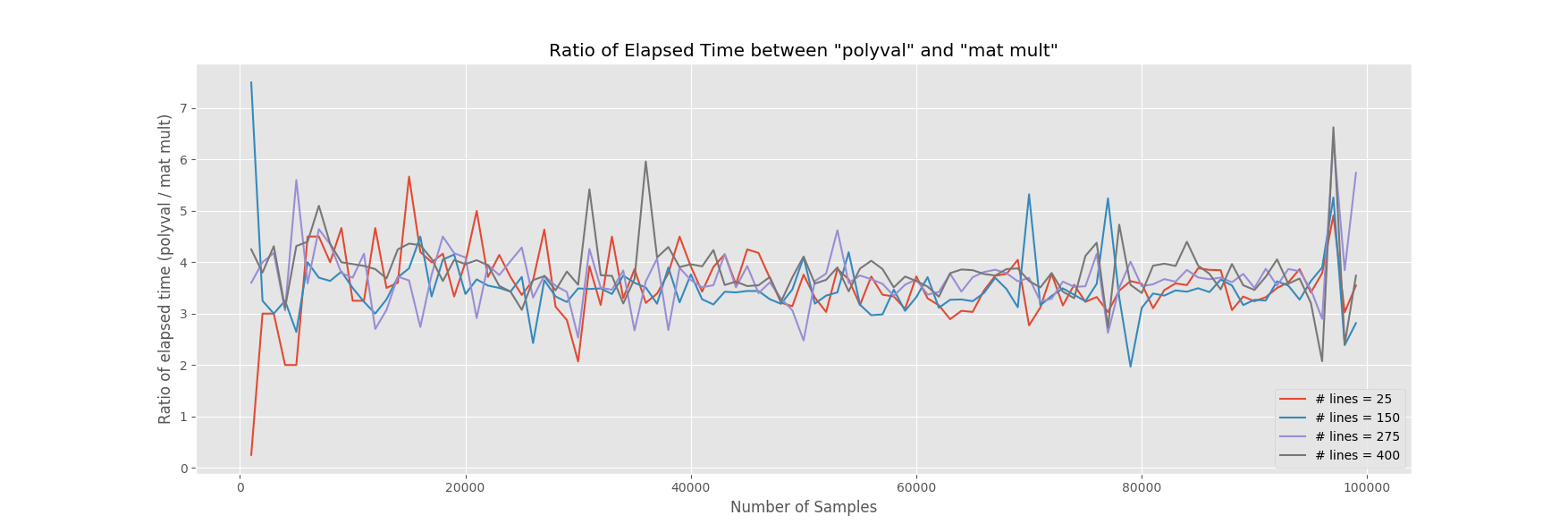
однако, если "speediest" - это то, что вы ищете, просто построение полиномиальных входов и использование рудиментарных функций умножения матрицы numpy приводит к несколько более быстрым ( примерно в 4 раза быстрее) вычислительным скоростям.

настройка

используя ту же настройку, что и выше, мы создадим 25 разных строк арматура.

>>> num_samples = 100000
>>> num_lines = 100
>>> x = np.random.randint(0,100,num_samples)
>>> y = np.random.randint(0,100,(num_samples, num_lines))
>>> fit = np.polyfit(x,y,deg=2)
>>> xx = np.random.randint(0,100,num_samples*10)

библиотеки numpy это polyval функции

res1 = np.polynomial.polynomial.polyval(xx, fit)

Умножение Базовой Матрицы

inputs = np.array([np.power(xx,d) for d in range(len(fit))])
res2 = fit.T.dot(inputs)

времени функции

используя те же параметры выше... 

%timeit _ = np.polynomial.polynomial.polyval(xx, fit)
1 loop, best of 3: 247 ms per loop

%timeit inputs = np.array([np.power(xx, d) for d in range(len(fit))]);_ = fit.T.dot(inputs)
10 loops, best of 3: 72.8 ms per loop

бить мертвую лошадь...

enter image description here

средний Рему эффективности ~3.61 X более быстро. Колебания скорости, вероятно, происходят от случайных компьютерных процессов в фоновом режиме.

0