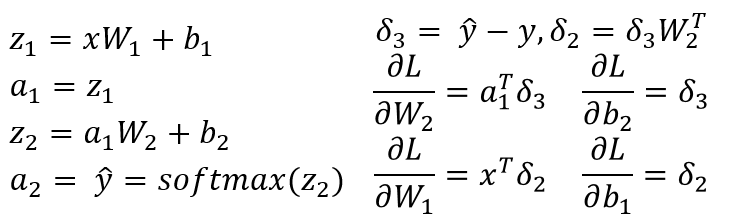numpy: вычислить производную функции softmax
я пытаюсь понять backpropagation в простой 3-х слоистой нейронной сети с MNIST.
есть входной слой с weights и bias. Этикетки MNIST это 10 вектор класса.
второй слой-это linear tranform. Третий слой -softmax activation чтобы получить результат Как вероятности.
Backpropagation вычисляет производную на каждом шаге и называете это градиент.
предыдущие слои добавляет global или previous градиент к local gradient. У меня возникли проблемы с вычислением local gradient на softmax
несколько ресурсов в интернете проходят через объяснение softmax и его производных и даже дают образцы кода самого softmax
def softmax(x):
"""Compute the softmax of vector x."""
exps = np.exp(x)
return exps / np.sum(exps)
производная объясняется относительно when i = j и когда i != j. Это простой фрагмент кода, который я придумал и надеялся проверить мой понимание:
def softmax(self, x):
"""Compute the softmax of vector x."""
exps = np.exp(x)
return exps / np.sum(exps)
def forward(self):
# self.input is a vector of length 10
# and is the output of
# (w * x) + b
self.value = self.softmax(self.input)
def backward(self):
for i in range(len(self.value)):
for j in range(len(self.input)):
if i == j:
self.gradient[i] = self.value[i] * (1-self.input[i))
else:
self.gradient[i] = -self.value[i]*self.input[j]
затем self.gradient - это local gradient, который является вектором. Правильно ли это? Есть ли лучший способ написания этого?
3 ответов
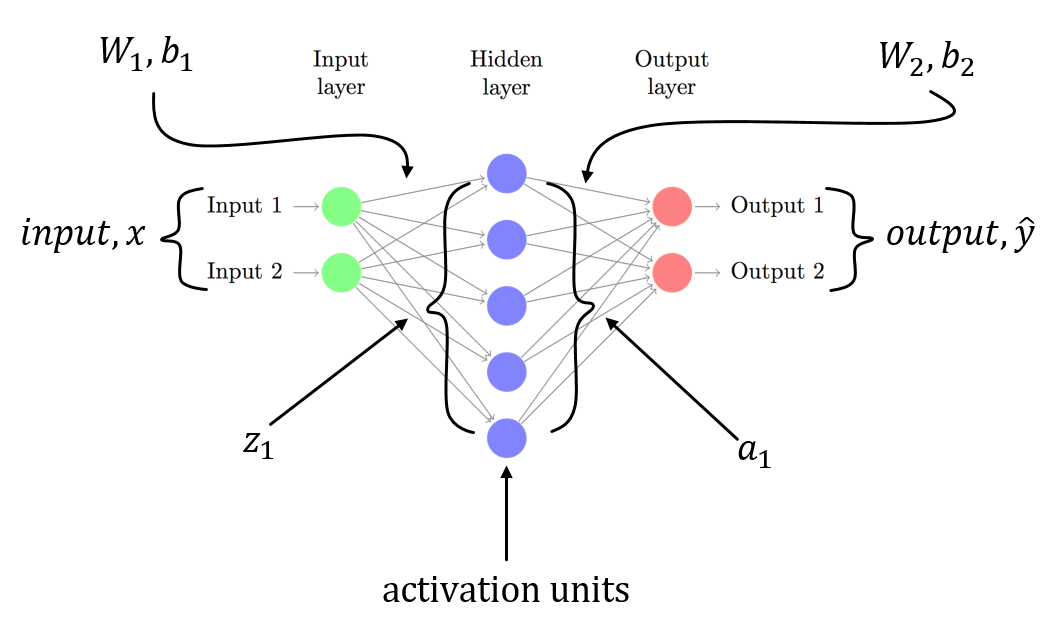
Я предполагаю, что у вас есть 3-слойный NN с W1, b1 for связано с линейным преобразованием из входного слоя в скрытый слой и W2, b2 связан с линейным преобразованием из скрытого слоя в выходной слой. Z1 и Z2 - это входной вектор для скрытого слоя и выходного слоя. a1 и a2 представляет выход скрытого слоя и выходного слоя. a2 ваш прогнозируемый выход. delta3 и delta2 несколько ошибок (backpropagated), и вы можете увидеть градиенты функции потерь относительно параметров модели.
это общий сценарий для 3-слойного NN (входной слой, только один скрытый слой и один выходной слой). Вы можете выполнить описанную выше процедуру для вычисления градиентов, которые должны быть легко вычислены! С другой ответ на этот пост уже указал на проблему в коде, я не повторяюсь тот же.
как я уже сказал, У вас есть n^2 частные производные.
если вы делаете математику, вы увидите, что dSM[i]/dx[k] is SM[i] * (dx[i]/dx[k] - SM[i]) так что вы должны иметь:
if i == j:
self.gradient[i,j] = self.value[i] * (1-self.value[i])
else:
self.gradient[i,j] = -self.value[i] * self.value[j]
вместо
if i == j:
self.gradient[i] = self.value[i] * (1-self.input[i])
else:
self.gradient[i] = -self.value[i]*self.input[j]
кстати, это можно вычислить более сжато так:
SM = self.value.reshape((-1,1))
jac = np.diag(self.value) - np.dot(SM, SM.T)
np.exp не стабилен, потому что он имеет Inf. Таким образом, вы должны вычесть максимум в x.
def softmax(x):
"""Compute the softmax of vector x."""
exps = np.exp(x - x.max())
return exps / np.sum(exps)
Если x-матрица, проверьте функцию softmax в этом notebook(https://github.com/rickiepark/ml-learn/blob/master/notebooks/5.%20multi-layer%20perceptron.ipynb)