Объединение нескольких смежных прямоугольников в один многоугольник
фон: Я работаю над сайтом для небольшого торгового центра, который имеет несколько прямоугольных "единиц" в аренду. Когда приходит "магазин", он может арендовать один или несколько" единиц", и я хотел бы создать карту, состоящую из магазинов (без ненанесенных единиц)
4 ответов
О'Рурк изучил проблему, связанную с этой (наряду со многими другими, которые относятся к вычислительной геометрии) и, как следствие, создал очень красивый метод для ее эффективного решения. Его метод описан в статье уникальность ортогональных точек соединения и также ясно проиллюстрировано на http://www.cs.mcgill.ca / ~cs644/Godfried/2005/Fall/sdroui9/p0_introduction.html. Обратите внимание, что он говорит, что многоугольник не должен делиться вершинами чтобы применить этот метод, но это происходит очень часто в обсуждаемой здесь проблеме. Таким образом, все, что нам нужно сделать, это устранить вершины, которые являются общими. Обратите внимание, что это все еще создает многоугольник, и это многоугольник, который требуется в результате. Также обратите внимание, что список прямоугольников не должен содержать дубликатов (я предполагаю, что это так, иначе предварительно обработайте его, чтобы сделать список уникальным).
я использовал Python для его кода, и если есть какие-либо сомнения в его значении, не стесняйтесь спрашивать.
Ниже приводится обзор осуществления. Начнем со списка прямоугольников, описанных в соответствии с нотацией OP. Затем мы получаем четыре вершины каждого прямоугольника, отбрасывая общие вершины по пути. Это эффективно достигается с помощью set. Теперь мы просто применяем упомянутый алгоритм. Обратите внимание, что я использую две хэш-таблицы, edges_h (для горизонтальных углов) и edges_v (для вертикальных ребер) для хранения ребер многоугольника. Эти хэш-таблицы эффективно работают как неориентированный граф. Таким образом, после получения всех ребер легко и быстро получить упорядоченные вершины многоугольника. Выберите любой (ключ, значение) из хэш-таблицы edges_h, например. Теперь следующая упорядоченная вершина-это вершина, заданная edges_v[value] = next_value и далее по edges_h[next_value] и так далее. Повторите этот процесс, пока мы не достигнем первой выбранной вершины, и это будет сделано.
быстрый взгляд на упомянутый алгоритм:
- сортировка точек по наименьшему x, наименьшему y
- пройдите через каждый столбец и создайте ребра между вершинами 2i и 2i + 1 в этом столбце
- сортировка точек по наименьшему y, наименьшему x
- пройдите через каждую строку и создайте ребра между вершинами 2i и 2i + 1 в этой строке.
# These rectangles resemble the OP's illustration.
rect = ([[0, 10], [10, 0]],
[[10, 13], [19, 0]],
[[19, 10], [23, 0]])
points = set()
for (x1, y1), (x2, y2) in rect:
for pt in ((x1, y1), (x2, y1), (x2, y2), (x1, y2)):
if pt in points: # Shared vertice, remove it.
points.remove(pt)
else:
points.add(pt)
points = list(points)
def y_then_x(a, b):
if a[1] < b[1] or (a[1] == b[1] and a[0] < b[0]):
return -1
elif a == b:
return 0
else:
return 1
sort_x = sorted(points)
sort_y = sorted(points, cmp=y_then_x)
edges_h = {}
edges_v = {}
i = 0
while i < len(points):
curr_y = sort_y[i][1]
while i < len(points) and sort_y[i][1] == curr_y: //6chars comments, remove it
edges_h[sort_y[i]] = sort_y[i + 1]
edges_h[sort_y[i + 1]] = sort_y[i]
i += 2
i = 0
while i < len(points):
curr_x = sort_x[i][0]
while i < len(points) and sort_x[i][0] == curr_x:
edges_v[sort_x[i]] = sort_x[i + 1]
edges_v[sort_x[i + 1]] = sort_x[i]
i += 2
# Get all the polygons.
p = []
while edges_h:
# We can start with any point.
polygon = [(edges_h.popitem()[0], 0)]
while True:
curr, e = polygon[-1]
if e == 0:
next_vertex = edges_v.pop(curr)
polygon.append((next_vertex, 1))
else:
next_vertex = edges_h.pop(curr)
polygon.append((next_vertex, 0))
if polygon[-1] == polygon[0]:
# Closed polygon
polygon.pop()
break
# Remove implementation-markers from the polygon.
poly = [point for point, _ in polygon]
for vertex in poly:
if vertex in edges_h: edges_h.pop(vertex)
if vertex in edges_v: edges_v.pop(vertex)
p.append(poly)
for poly in p:
print poly
результатом является список упорядоченных вершин многоугольника:
[(0, 0), (0, 10), (10, 10), (10, 13), (19, 13), (19, 10), (23, 10), (23, 0)]
мы также можем поэкспериментировать с более сложным макетом:
rect = ([[1, 2], [3, 1]], [[1, 4], [2, 2]], [[1, 6], [2, 4]], [[2, 6], [3, 5]],
[[3, 8], [4, 4]], [[2, 8], [3, 7]], [[3, 10], [5, 8]], [[3, 4], [9, 3]],
[[4, 5], [7, 4]], [[6, 8], [7, 5]], [[6, 9], [8, 8]], [[8, 9], [10, 6]],
[[9, 6], [10, 3]])
что представлен в виде следующего набора прямоугольников:
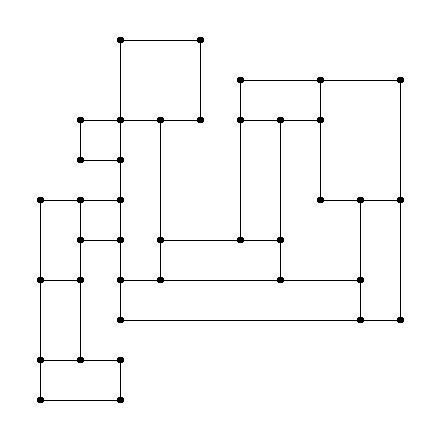
и метод производит следующие списки:
[(6, 9), (6, 5), (4, 5), (4, 8), (5, 8), (5, 10), (3, 10), (3, 8),
(2, 8), (2, 7), (3, 7), (3, 6), (1, 6), (1, 1), (3, 1), (3, 2),
(2, 2), (2, 5), (3, 5), (3, 3), (10, 3), (10, 9)]
[(9, 4), (9, 6), (8, 6), (8, 8), (7, 8), (7, 4)]
который, если он нарисован, представляет полигоны в синем и красном соответственно, как в:
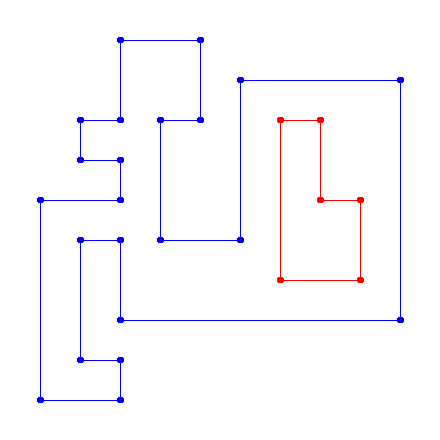
как простые ориентиры идут:
- 1000 прямоугольников: ~ 0.04 секунд
- 10000 прямоугольников: ~ 0.62 секунд
- 100000 прямоугольников: ~ 8.68 секунды!--22-->
эти тайминги просто в среднем 10 запусков на занятой устаревшей машине. Прямоугольники генерировались случайным образом.
EDIT:
реализация в PHP при необходимости.
вот мое решение:
RectUnion.в PHP
<?php
class RectUnion {
private $x, $y;
private $sides;
private $points;
function __construct() {
$this->x = array();
$this->y = array();
$this->sides = array();
$this->points = array();
}
function addRect($r) {
extract($r);
$this->x[] = $x1;
$this->x[] = $x2;
$this->y[] = $y1;
$this->y[] = $y2;
if ($x1 > $x2) { $tmp = $x1; $x1 = $x2; $x2 = $tmp; }
if ($y1 > $y2) { $tmp = $y1; $y1 = $y2; $y2 = $tmp; }
$this->sides[] = array($x1, $y1, $x2, $y1);
$this->sides[] = array($x2, $y1, $x2, $y2);
$this->sides[] = array($x1, $y2, $x2, $y2);
$this->sides[] = array($x1, $y1, $x1, $y2);
}
function splitSides() {
$result = array();
$this->x = array_unique($this->x);
$this->y = array_unique($this->y);
sort($this->x);
sort($this->y);
foreach ($this->sides as $i => $s) {
if ($s[0] - $s[2]) { // Horizontal
foreach ($this->x as $xx) {
if (($xx > $s[0]) && ($xx < $s[2])) {
$result[] = array($s[0], $s[1], $xx, $s[3]);
$s[0] = $xx;
}
}
} else { // Vertical
foreach ($this->y as $yy) {
if (($yy > $s[1]) && ($yy < $s[3])) {
$result[] = array($s[0], $s[1], $s[2], $yy);
$s[1] = $yy;
}
}
}
$result[] = $s;
}
return($result);
}
function removeDuplicates($sides) {
$x = array();
foreach ($sides as $i => $s) {
@$x[$s[0].','.$s[1].','.$s[2].','.$s[3]]++;
}
foreach ($x as $s => $n) {
if ($n > 1) {
unset($x[$s]);
} else {
$this->points[] = explode(",", $s);
}
}
return($x);
}
function drawPoints($points, $outfile = null) {
$xs = $this->x[count($this->x) - 1] + $this->x[0];
$ys = $this->y[count($this->y) - 1] + $this->y[0];
$img = imagecreate($xs, $ys);
if ($img !== FALSE) {
$wht = imagecolorallocate($img, 255, 255, 255);
$blk = imagecolorallocate($img, 0, 0, 0);
$red = imagecolorallocate($img, 255, 0, 0);
imagerectangle($img, 0, 0, $xs - 1, $ys - 1, $red);
$oldp = $points[0];
for ($i = 1; $i < count($points); $i++) {
$p = $points[$i];
imageline($img, $oldp['x'], $oldp['y'], $p['x'], $p['y'], $blk);
$oldp = $p;
}
imageline($img, $oldp['x'], $oldp['y'], $points[0]['x'], $points[0]['y'], $blk);
if ($outfile == null) header("content-type: image/png");
imagepng($img, $outfile);
imagedestroy($img);
}
}
function drawSides($sides, $outfile = null) {
$xs = $this->x[count($this->x) - 1] + $this->x[0];
$ys = $this->y[count($this->y) - 1] + $this->y[0];
$img = imagecreate($xs, $ys);
if ($img !== FALSE) {
$wht = imagecolorallocate($img, 255, 255, 255);
$blk = imagecolorallocate($img, 0, 0, 0);
$red = imagecolorallocate($img, 255, 0, 0);
imagerectangle($img, 0, 0, $xs - 1, $ys - 1, $red);
foreach ($sides as $s => $n) {
if (is_array($n)) {
$r = $n;
} else {
$r = explode(",", $s);
}
imageline($img, $r['x1'], $r['y1'], $r['x2'], $r['y2'], $blk);
}
if ($outfile == null) header("content-type: image/png");
imagepng($img, $outfile);
imagedestroy($img);
}
}
function getSides($sides = FALSE) {
if ($sides === FALSE) {
foreach ($this->sides as $r) {
$result[] = array('x1' => $r[0], 'y1' => $r[1], 'x2' => $r[2], 'y2' => $r[3]);
}
} else {
$result = array();
foreach ($sides as $s => $n) {
$r = explode(",", $s);
$result[] = array('x1' => $r[0], 'y1' => $r[1], 'x2' => $r[2], 'y2' => $r[3]);
}
}
return($result);
}
private function _nextPoint(&$points, $lastpt) {
@extract($lastpt);
foreach ($points as $i => $p) {
if (($p[0] == $x) && ($p[1] == $y)) {
unset($points[$i]);
return(array('x' => $p[2], 'y' => $p[3]));
} else if (($p[2] == $x) && ($p[3] == $y)) {
unset($points[$i]);
return(array('x' => $p[0], 'y' => $p[1]));
}
}
return false;
}
function getPoints($points = FALSE) {
if ($points === FALSE) $points = $this->points;
$result = array(
array('x' => $points[0][0], 'y' => $points[0][1])
);
$lastpt = array('x' => $points[0][2], 'y' => $points[0][3]);
unset($points[0]);
do {
$result[] = $lastpt;
} while ($lastpt = $this->_nextPoint($points, $lastpt));
return($result);
}
}
?>
слияние.в PHP
<?php
require_once("RectUnion.php");
function generateRect($prev, $step) {
$rect = array(
'x1' => $prev['x2'],
'x2' => $prev['x2'] + rand($step, $step * 10),
'y1' => rand($prev['y1'] + 2, $prev['y2'] - 2),
'y2' => rand($step * 2, $step * 10)
);
return($rect);
}
$x0 = 50; // Pixels
$y0 = 50; // Pixels
$step = 20; // Pixels
$nrect = 10; // Number of rectangles
$rects = array(
array("x1" => 50, "y1" => 50, "x2" => 100, "y2" => 100)
);
for ($i = 1; $i < $nrect - 1; $i++) {
$rects[$i] = generateRect($rects[$i - 1], $step);
}
$start_tm = microtime(true);
$ru = new RectUnion();
foreach ($rects as $r) {
$ru->addRect($r);
}
$union = $ru->removeDuplicates($ru->splitSides());
$stop_tm = microtime(true);
$ru->drawSides($ru->getSides(), "before.png");
if (FALSE) { // Lines
$sides = $ru->getSides($union);
$ru->drawSides($sides, "after.png");
} else { // Points
$points = $ru->getPoints();
$ru->drawPoints($points, "after.png");
}
?>
<!DOCTYPE html>
<html>
<body>
<fieldset>
<legend>Before Union</legend>
<img src='before.png'>
</fieldset>
<fieldset>
<legend>After Union</legend>
<img src='after.png'>
</fieldset>
<h4>Elapsed Time: <?= round($stop_tm - $start_tm, 4) ?> seconds</h4>
<?php if (isset($sides)): ?>
<h4>Sides:</h4>
<pre><?= print_r($sides, true) ?></pre>
<?php elseif (isset($points)): ?>
<h4>Points:</h4>
<pre><?= print_r($points, true) ?></pre>
<?php endif ?>
</body>
</html>
как это работает?
скрипт идентифицирует и удаляет все "перекрытия" сегментов. Например: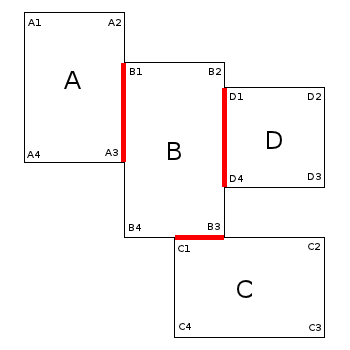
во-первых, стороны каждого прямоугольника разделены на пересечениях со сторонами adiacent прямоугольника.
Например, рассмотрим сторону B2-B3 прямоугольника B: метод " splitSides разбивает его на сегменты B2-D1, D1-D4 и D4-B3.
Затем метод "removeDuplicates" удаляет все перекрывающиеся (дублирующиеся) сегменты.
Например, сегмент D1-D4 является дубликатом, так как он отображается либо в прямоугольнике B, либо в прямоугольнике D.
Наконец, метод " getSides "возвращает список оставшихся сегментов, а метод" getPoints " возвращает список точек многоугольника.
Методы "draw" предназначены только для графического представления результат, и требовать расширение GD работает:
о работе
вот несколько раз выполнения:
- 10 прямоугольников: 0,003 секунды
- 100 прямоугольников: 0,220 секунды
- 1000 прямоугольников: 4,407 секунд
- 2000 прямоугольников: 13,448 секунд
путем профилирования выполнения с помощью отладчик xdebug, у меня есть следующие результаты:
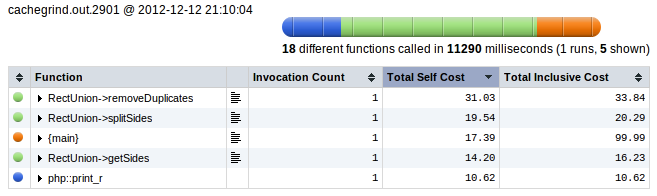
Я не буду использовать математику для решения этой проблемы, а только анализ.
рассмотрим следующее изображение :
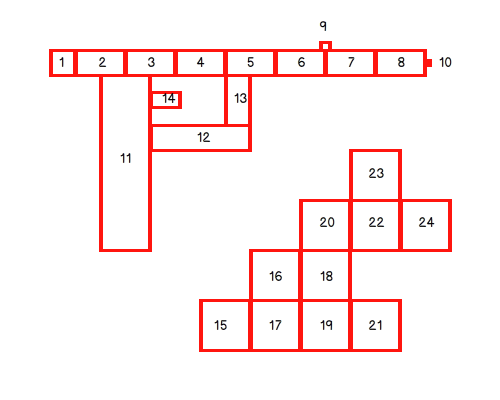
здесь у нас есть 2 примера сразу, чтобы быть уверенными, что мы рассмотрим все случаи.
на первом изображении у нас есть особый случай : прямоугольников нет 3, 4, 5, 11, 12, 13 создает пустую область, это может быть пространство дыма в вашем случае.
во втором изображении у нас есть угол между прямоугольниками № 16, 17, 18, 19... это будет иметь значение позже.
как я решил проблему использует следующие вещи :
угол-это точка, которая была записана от 2 до 8 раз : по крайней мере 2, потому что, если мы представим прямоугольник ABCD, угол B будет разделен с AB и BC (поэтому пиксель был помещен 2 раза). Он может быть записан в 8 раз в случае прямоугольников, 16, 17, 18, 19, где одна точка является общей с 4 прямоугольника, поэтому 8 сторон.
сторона-это набор точек, которые можно записать 1 или 2 раза (без учета углов) : 1 раз, если сторона одна, а не близко к другой стороне, и 2 раза, если сторона близка к другой. И сторона, которая не близка к другой, близка к внешней: она должна принимать часть конечного многоугольника.
Итак, вот логика:
- мы создаем виртуальное пространство того же размера, что и все изображение, заполненное нулями (0 ).
-
мы пишем все прямоугольники, но вместо записи пикселей мы увеличиваем значение виртуального пикселя
21111111112 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2111111111622222222261111111112 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 21111111116222222222611111111141111111112 1 2 1 1 2 1 1 2 1 1 2 1 1 2 1 1 2 1 1 2 1 1 2 1 1 2 1 (...)
(извините, похоже, что у моего отступа есть проблемы с инструментом форматирования SO)
- мы удаляем все виртуальные точки, которые имеют значение больше 2, за исключением углов, которые мы установили в 1
на данный момент, у нас одни полигоны и точки (где есть угол в середине нескольких других прямоугольников).
11111111111
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
11111111111 11111111111
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
11111111111 111111111111111111111
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
11111111111 1 11111111111
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
11111111111111111111111111111111111111111
теперь нам нужно искать один или несколько полигонов (у нас может быть несколько полигонов, когда мы находимся в случае 11 12 13 14 3 4 5 прямоугольников). Это значит, искать точку в нашем виртуальном образе.
если точка одна (см. выше), у нее нет точки вверху, слева, внизу или справа, это угол (мы сохранили наш угол ранее) в середине нескольких другие прямоугольники. Это довольно сложно, но работает, если все ваши прямоугольники больше 4 пикселей.
когда мы находим точку, мы сохраняем ее, пытаемся повторить одно направление (сверху / слева/справа / снизу) и идти вперед, удаляя точки в этом направлении, пока не будет больше точки : это один угол многоугольника. Мы продолжаем этот путь до тех пор, пока невозможно двигаться в любом направлении : это означает, что мы находимся в конце многоугольника.
теперь, вы получаете 2-мерный массив: первое измерение-это список полигонов (в случае первого примера), а второе измерение-список точек, описывающих ваш многоугольник. Для каждого полигона вам просто нужно перебрать эти точки и присоединить текущую к следующей, чтобы получить полигон.
как насчет результата сейчас ?
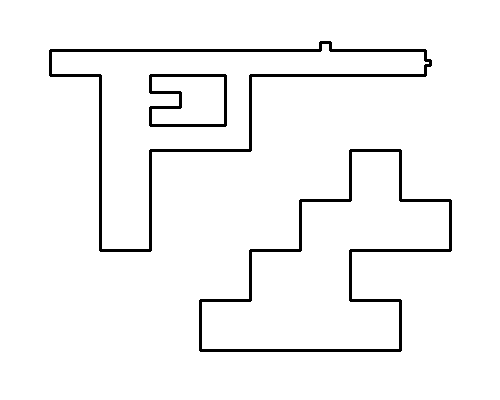
реализация :
class PolygonMaker
{
private $image;
private $width;
private $height;
private $vImage;
public function __construct($width, $height)
{
// create a GD image to display results and debug
$this->width = $width;
$this->height = $height;
$this->image = imagecreatetruecolor($width, $height);
$white = imagecolorallocate($this->image, 0xFF, 0xFF, 0xFF);
imagefill($this->image, 0, 0, $white);
imagesetthickness($this->image, 3);
}
public function __destruct()
{
imagedestroy($this->image);
}
public function display()
{
// Display gd image as png
header("Content-type: image/png");
imagepng($this->image);
}
public function drawRectangles(array $rectangles, $r, $g, $b)
{
// Draw rectangles as they are inside the gd image
foreach ($rectangles as $rectangle)
{
list($tx, $ty) = $rectangle[0];
list($bx, $by) = $rectangle[1];
$color = imagecolorallocate($this->image, $r, $g, $b);
imagerectangle($this->image, $tx, $ty, $bx, $by, $color);
}
}
public function findPolygonsPoints(array $rectangles)
{
// Create a virtual image where rectangles will be "drawn"
$this->_createVirtualImage($rectangles);
$polygons = array ();
// Searches for all polygons inside the virtual image
while (!is_null($beginPoint = $this->_findPolygon()))
{
$polygon = array ();
// Push the first point
$polygon[] = $this->_cleanAndReturnPolygonPoint($beginPoint);
$point = $beginPoint;
// Try to go up, down, left, right until there is no more point
while ($point = $this->_getNextPolygonPoint($point))
{
// Push the found point
$polygon[] = $this->_cleanAndReturnPolygonPoint($point);
}
// Push the first point at the end to close polygon
$polygon[] = $beginPoint;
// Add the polygon to the list, in case of several polygons in the image
$polygons[] = $polygon;
}
$this->vImage = null;
return $polygons;
}
private function _createVirtualImage(array $rectangles)
{
// Create a 0-filled grid where will be stored rectangles
$this->vImage = array_fill(0, $this->height, array_fill(0, $this->width, 0));
// Draw each rectangle to that grid (each pixel increments the corresponding value of the grid of 1)
foreach ($rectangles as $rectangle)
{
list($x1, $y1, $x2, $y2) = array ($rectangle[0][0], $rectangle[0][1], $rectangle[1][0], $rectangle[1][1]);
$this->_drawVirtualLine($x1, $y1, $x1, $y2); // top-left, bottom-left
$this->_drawVirtualLine($x2, $y1, $x2, $y2); // top-right, bottom-right
$this->_drawVirtualLine($x1, $y1, $x2, $y1); // top-left, top-right
$this->_drawVirtualLine($x1, $y2, $x2, $y2); // bottom-left, bottom-right
}
// Remove all pixels that are scored > 1 (that's our logic!)
for ($y = 0; ($y < $this->height); $y++)
{
for ($x = 0; ($x < $this->width); $x++)
{
$value = &$this->vImage[$y][$x];
$value = $value > 1 ? 0 : $value;
}
}
}
private function _drawVirtualLine($x1, $y1, $x2, $y2)
{
// Draw a vertial line in the virtual image
if ($x1 == $x2)
{
if ($y1 > $y2)
{
list($x1, $y1, $x2, $y2) = array ($x2, $y2, $x1, $y1);
}
for ($y = $y1; ($y <= $y2); $y++)
{
$this->vImage[$y][$x1]++;
}
}
// Draw an horizontal line in the virtual image
if ($y1 == $y2)
{
if ($x1 > $x2)
{
list($x1, $y1, $x2, $y2) = array ($x2, $y2, $x1, $y1);
}
for ($x = $x1; ($x <= $x2); $x++)
{
$this->vImage[$y1][$x]++;
}
}
// Force corners to be 1 (because one corner is at least used 2 times but we don't want to remove them)
$this->vImage[$y1][$x1] = 1;
$this->vImage[$y1][$x2] = 1;
$this->vImage[$y2][$x1] = 1;
$this->vImage[$y2][$x2] = 1;
}
private function _findPolygon()
{
// We're looking for the first point in the virtual image
foreach ($this->vImage as $y => $row)
{
foreach ($row as $x => $value)
{
if ($value == 1)
{
// Removes alone points ( every corner have been set to 1, but some corners are alone (eg: middle of 4 rectangles)
if ((!$this->_hasPixelAtBottom($x, $y)) && (!$this->_hasPixelAtTop($x, $y))
&& (!$this->_hasPixelAtRight($x, $y)) && (!$this->_hasPixelAtLeft($x, $y)))
{
$this->vImage[$y][$x] = 0;
continue;
}
return array ($x, $y);
}
}
}
return null;
}
private function _hasPixelAtBottom($x, $y)
{
// The closest bottom point is a point positionned at (x, y + 1)
return $this->_hasPixelAt($x, $y + 1);
}
private function _hasPixelAtTop($x, $y)
{
// The closest top point is a point positionned at (x, y - 1)
return $this->_hasPixelAt($x, $y - 1);
}
private function _hasPixelAtLeft($x, $y)
{
// The closest left point is a point positionned at (x - 1, y)
return $this->_hasPixelAt($x - 1, $y);
}
private function _hasPixelAtRight($x, $y)
{
// The closest right point is a point positionned at (x + 1, y)
return $this->_hasPixelAt($x + 1, $y);
}
private function _hasPixelAt($x, $y)
{
// Check if the pixel (x, y) exists
return ((isset($this->vImage[$y])) && (isset($this->vImage[$y][$x])) && ($this->vImage[$y][$x] > 0));
}
private function _cleanAndReturnPolygonPoint(array $point)
{
// Remove a point from the virtual image
list($x, $y) = $point;
$this->vImage[$y][$x] = 0;
return $point;
}
private function _getNextPolygonPoint(array $point)
{
list($x, $y) = $point;
// Initialize modifiers, to move to the right, bottom, left or top.
$directions = array(
array(1, 0), // right
array(0, 1), // bottom
array(-1, 0), // left
array(0, -1), // top
);
// Try to get to one direction, if we can go ahead, there is a following corner
$return = null;
foreach ($directions as $direction)
{
list($xModifier, $yModifier) = $direction;
if (($return = $this->_iterateDirection($x, $y, $xModifier, $yModifier)) !== null)
{
return $return;
}
}
// the point is alone : we are at the end of the polygon
return $return;
}
private function _iterateDirection($x, $y, $xModifier, $yModifier)
{
// This method follows points in a direction until the last point
$return = null;
while ($this->_hasPixelAt($x + $xModifier, $y + $yModifier))
{
$x = $x + $xModifier;
$y = $y + $yModifier;
// Important : we remove the point so we'll not get back when moving
$return = $this->_cleanAndReturnPolygonPoint(array ($x, $y));
}
// The last point is a corner of the polygon because if it has no following point, we change direction
return $return;
}
/**
* This method draws a polygon with the given points. That's to check if
* our calculations are valid.
*
* @param array $points An array of points that define the polygon
*/
public function drawPolygon(array $points, $r, $g, $b)
{
$count = count($points);
for ($i = 0; ($i < $count); $i++)
{
// Draws a line between the current and the next point until the last point is reached
if (array_key_exists($i + 1, $points))
{
list($x1, $y1) = $points[$i];
list($x2, $y2) = $points[$i + 1];
$black = imagecolorallocate($this->image, $r, $g, $b);
imageline($this->image, $x1, $y1, $x2, $y2, $black);
}
}
}
}
пример использования :
$rectanglesA = array (
array ( // 1
array (50, 50), // tx, ty
array (75, 75), // bx, by
),
array ( // 2
array (75, 50), // tx, ty
array (125, 75), // bx, by
),
array ( // 3
array (125, 50), // tx, ty
array (175, 75), // bx, by
),
array ( // 4
array (175, 50), // tx, ty
array (225, 75), // bx, by
),
array ( // 5
array (225, 50), // tx, ty
array (275, 75), // bx, by
),
array ( // 6
array (275, 50), // tx, ty
array (325, 75), // bx, by
),
array ( // 7
array (325, 50), // tx, ty
array (375, 75), // bx, by
),
array ( // 8
array (375, 50), // tx, ty
array (425, 75), // bx, by
),
array ( // 9
array (320, 42), // tx, ty
array (330, 50), // bx, by
),
array ( // 10
array (425, 60), // tx, ty
array (430, 65), // bx, by
),
array ( // 11
array (100, 75), // tx, ty
array (150, 250), // bx, by
),
array ( // 12
array (150, 125), // tx, ty
array (250, 150), // bx, by
),
array ( // 13
array (225, 75), // tx, ty
array (250, 125), // bx, by
),
array ( // 14
array (150, 92), // tx, ty
array (180, 107), // bx, by
),
);
$rectanglesB = array (
array ( // 15
array (200, 300), // tx, ty
array (250, 350), // bx, by
),
array ( // 16
array (250, 250), // tx, ty
array (300, 300), // bx, by
),
array ( // 17
array (250, 300), // tx, ty
array (300, 350), // bx, by
),
array ( // 18
array (300, 250), // tx, ty
array (350, 300), // bx, by
),
array ( // 19
array (300, 300), // tx, ty
array (350, 350), // bx, by
),
array ( // 20
array (300, 200), // tx, ty
array (350, 250), // bx, by
),
array ( // 21
array (350, 300), // tx, ty
array (400, 350), // bx, by
),
array ( // 22
array (350, 200), // tx, ty
array (400, 250), // bx, by
),
array ( // 23
array (350, 150), // tx, ty
array (400, 200), // bx, by
),
array ( // 24
array (400, 200), // tx, ty
array (450, 250), // bx, by
),
);
$polygonMaker = new PolygonMaker(500, 400);
// Just to get started and see what's happens
//$polygonMaker->drawRectangles($rectanglesA, 0xFF, 0x00, 0x00);
//$polygonMaker->drawRectangles($rectanglesB, 0xFF, 0x00, 0x00);
$polygonsA = $polygonMaker->findPolygonsPoints($rectanglesA);
foreach ($polygonsA as $polygon)
{
$polygonMaker->drawPolygon($polygon, 0x00, 0x00, 0x00);
}
$polygonsB = $polygonMaker->findPolygonsPoints($rectanglesB);
foreach ($polygonsB as $polygon)
{
$polygonMaker->drawPolygon($polygon, 0x00, 0x00, 0x00);
}
// Display image to see if everything is correct
$polygonMaker->display();
просто некоторые мысли:
- повторите все углы, чтобы найти тот, который инцидент только с одной единицей, и, следовательно, угол вашего союза.
- оттуда выберите одно направление для итерации, например, всегда против часовой стрелки.
- проверьте, является ли край в этом направлении инцидентом с углом другого блока или следующий угол вдоль этого края инцидентом с краем другого блока. Любой из них будет следующим углом союз. В противном случае конечная точка этого края-следующий угол.
- продолжайте таким образом, переходя от одной единицы к другой, пока не достигнете начальной точки.
