Обнаружение угловых координат выпуклого многоугольника в порядке по часовой стрелке MATLAB
у меня есть некоторые изображения, которые включают в себя как выпуклые, так и невыпуклые многоугольники. Каждое изображение содержит ровно один полигон. Мне нужно определить угловые координаты и отсортировать их по часам или против часовой стрелки. Для выпуклых полигонов я использую обнаружение угла Харриса для определения углов и convexhull для сортировки точек. Но я понятия не имею, как сортировать выпуклый многоугольник. Поскольку мои входы-это изображения, я думаю, что некоторые изображения Обработка техника может помочь отсортировать их, перемещаясь вдоль края многоугольника. Есть ли способ с наименьшей сложностью?
Изображение:
я назвал углы случайным образом.

ожидаемый результат:
Я ожидаю угловые координаты в этом порядке
1 3 5 9 4 2 8 7 6 10 или 1 10 6 7 8 2 4 9 5 3. Вы можете начать в любой момент, не обязательно 1
изменить 1:
после rayryeng это решение, которое работает для всех выпуклых многоугольников, а также для некоторых выпуклых многоугольников, есть некоторые выпуклые многоугольники, которые не идут хорошо с его алгоритмом.
вот пример

2 ответов
другой подход заключается в использовании bwdistgeodesic чтобы найти порядок углов по их расстоянию вдоль вашего края. Это должно работать для любого полигона, где вы можете обнаружить непрерывное ребро.
мы начинаем с загрузки изображения из переполнения стека и преобразования его в черно-белое изображение, чтобы облегчить поиск края
A = imread('http://i.stack.imgur.com/dpbpP.jpg');
A_bw = im2bw(A,100/255); %binary image
A_bw1 = imcomplement(A_bw); %inverted binary image
на bwmorph функция предоставляет множество возможностей для управления черно-белыми изображениями. Мы собираемся использовать remove возможность найти край нашего многоугольника, но вы также можете использовать другой детектор края, если хотите.
%Find the edges
A_edges = bwmorph(A_bw, 'remove');
[edge_x, edge_y] = find(A_edges');
давайте визуализировать края, которые мы обнаружили
figure; imshow(A_edges);

хорошо, у нас есть хороший четкий непрерывный край. Теперь давайте найдем углы. Я использую corner, но вы можете заменить свой любимый угловой детектор
A_corners = corner(A_bw1, 'QualityLevel',.3);
давайте визуализировать наш начальный угол заказ
figure; imshow(A_bw1);
hold on
plot(A_corners(:,1), A_corners(:,2), 'r.', 'MarkerSize', 18)
text(A_corners(:,1), A_corners(:,2), strsplit(num2str(1:length(A_corners))), 'Color', 'g', 'FontSize', 24);
hold off
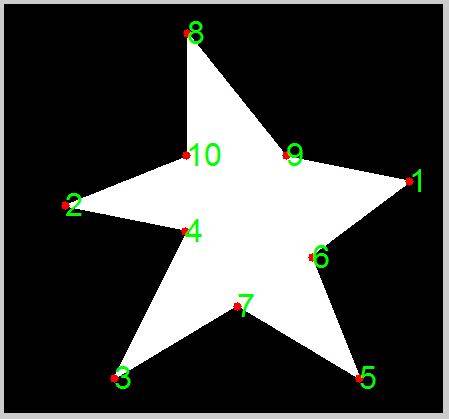
еще одна вещь, которую вы можете не заметить, это то, что они не находятся непосредственно по краям. Я начну с того, что найду ближайшую точку вдоль края к каждой угловой точке, а затем визуализирую углы красным цветом и ближайшие точки края зеленым.
[~, ind] = min(pdist2(A_corners, [edge_x, edge_y]), [], 2);
A_edge_corners = [edge_x(ind), edge_y(ind)];
figure; imshow(A_edges);
hold on;
plot(A_corners(:,1), A_corners(:,2), 'r.', 'MarkerSize', 18)
plot(A_edge_corners(:,1), A_edge_corners(:,2),'g.', 'MarkerSize', 18)
hold off;
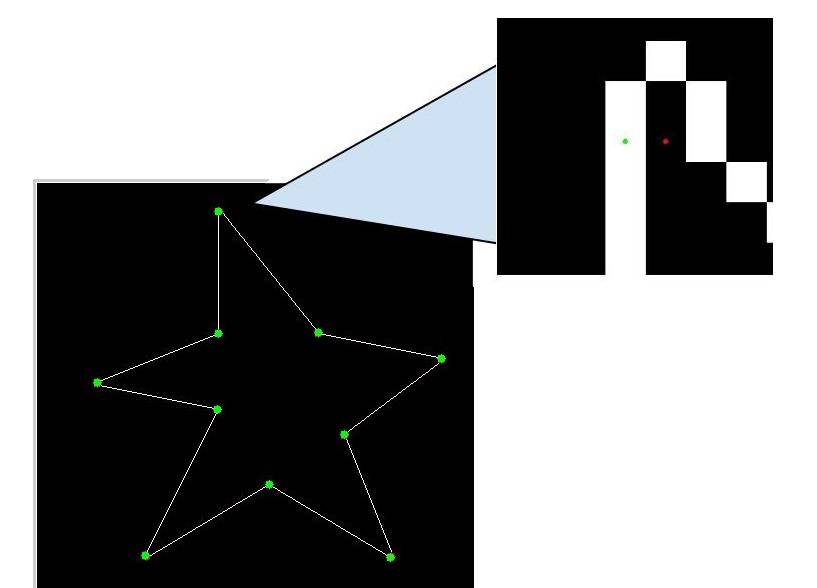
чтобы рассчитать расстояние вокруг края для каждого угла, мы будем использовать приближение угловой точки,A_edge_corners (Зеленая Точка) на краю а не сама угловая точка A_corners (красная точка).
теперь у нас есть все, что нам нужно использовать bwdistgeodesic. Эта функция находит расстояние до начальной точки для каждого ненулевого пикселя в черно-белом изображении. Нас интересует расстояние от начального угла до каждой точки На краю. Давай попробуем.
% Calculate distance from seed corner
first_corner = A_edge_corners(1,:);
D = bwdistgeodesic(A_edges, first_corner(1), first_corner(2));
figure; imagesc(D);
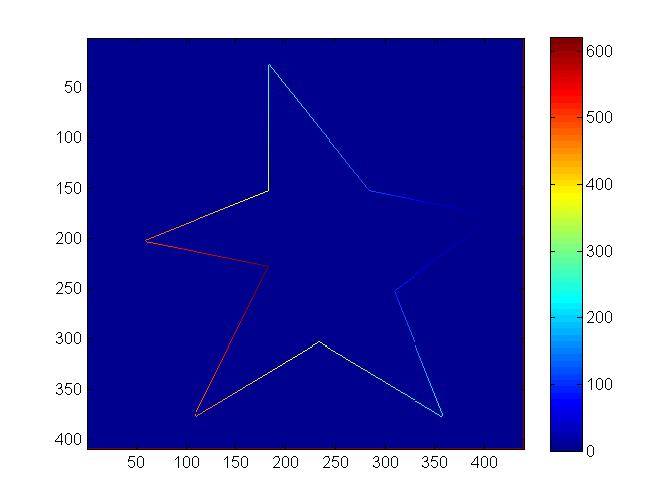
мы начинаем с самого правого угла, и пиксели, удаляющиеся от угла, увеличиваются в значении. Но это не совсем то, чего мы хотим. Если мы упорядочим углы, используя эти значения, мы получим упорядочение на расстоянии от начальной точки.
[~, corner_order] = sort(D(sub2ind(size(D), A_edge_corners(:,2), A_edge_corners(:,1))));
A_corners_reorder1 = A_corners(corner_order, :);
figure; imshow(A_bw1);
hold on
plot(A_corners_reorder1(:,1), A_corners_reorder1(:,2),'r.', 'MarkerSize', 18)
text(A_corners_reorder1(:,1), A_corners_reorder1(:,2), strsplit(num2str(1:length(A_corners))), 'Color', 'g', 'FontSize', 24);
hold off
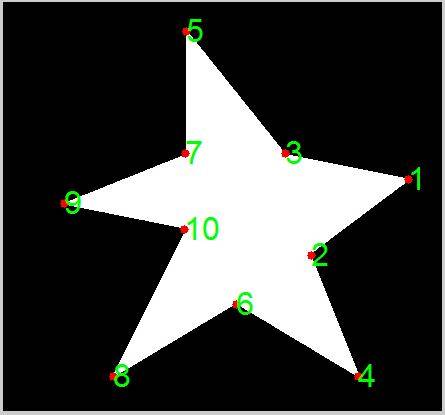
чтобы решить эту проблему, нам просто нужно сломать край, чтобы порядок шел только в одном направлении от начальной точки. Если вас интересует порядок по часовой стрелке или против часовой стрелки, вам нужно будет сломать край в соответствии с набором правил в зависимости от ориентации края. Если направление не имеет значения, вы можете просто найти соседний пиксель в начальном углу и сломать край там.
%Break the edge into one path by removing a pixel adjacent to first corner
%If the corner is near the edge of the image, you would need to check for
%edge conditions
window = A_edges(first_corner(2)-1:first_corner(2)+1, first_corner(1)-1:first_corner(1)+1);
window(2,2) = 0; %Exclude the corner itself
[x, y] = find(window, 1);
A_edges(first_corner(2)+x-2, first_corner(1)+y-2) = 0;
figure; imshow(A_edges);
hold on;
plot(first_corner(1), first_corner(2), 'r.', 'MarkerSize', 18)
hold off;
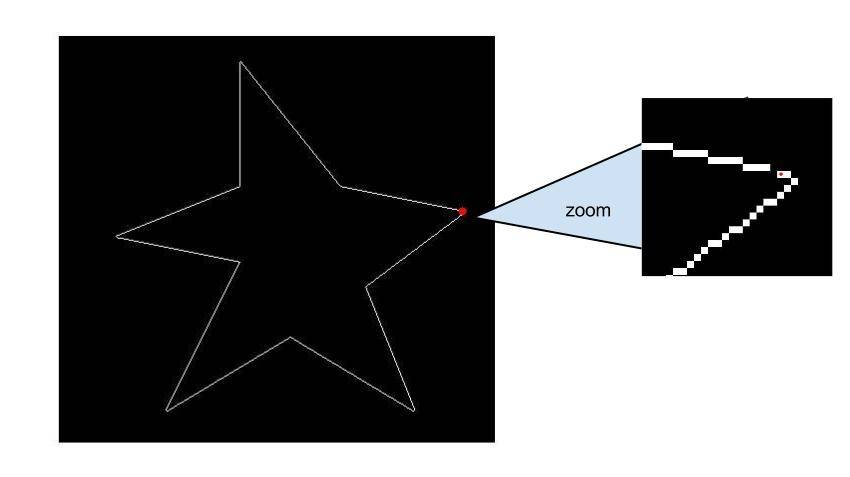
теперь расстояние от начальной точки вдоль края может следовать только по одному пути
%Find order the pixels along edge
D = bwdistgeodesic(A_edges, first_corner(1), first_corner(2));
figure; imagesc(D);
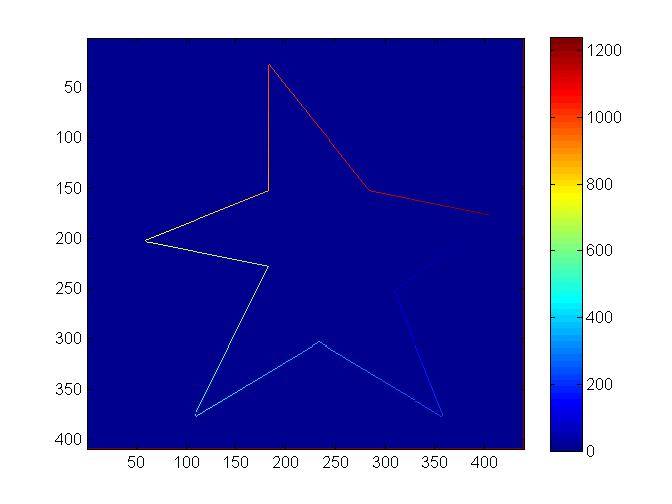
это дает нам желаемый порядок ребер
[~, corner_order] = sort(D(sub2ind(size(D), A_edge_corners(:,2), A_edge_corners(:,1))));
A_corners = A_corners(corner_order, :);
figure; imshow(A_bw1);
hold on
plot(A_corners(:,1), A_corners(:,2),'r.', 'MarkerSize', 18)
text(A_corners(:,1), A_corners(:,2), strsplit(num2str(1:length(A_corners))), 'Color', 'g', 'FontSize', 24);
hold off
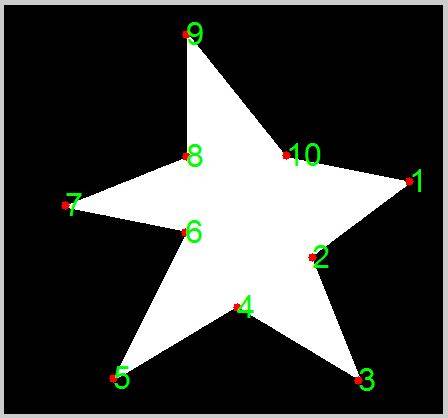
этот метод также работает на полигонах, которые несбалансированы относительно centroid, например, второе демо-изображение.

для удовольствия я представляю третье изображение, которое имеет вершину на противоположной стороне центроида, как более ясный пример несбалансированного многоугольника. Мой метод также правильно анализирует это изображение.

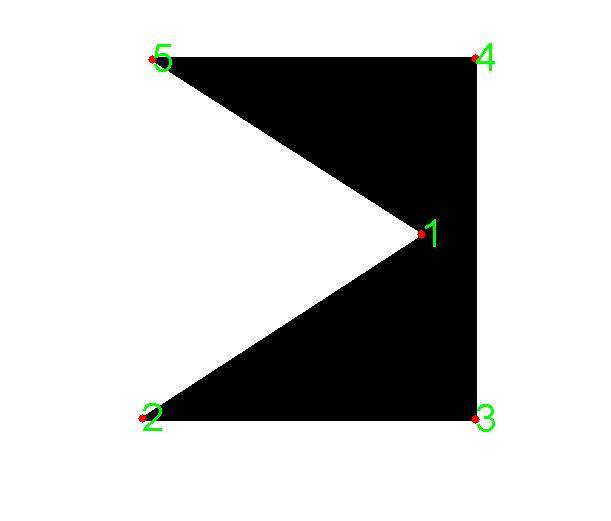
это распространенная проблема в обработке изображений. Типичный ответ-найти центроид фигуры и найти угол между центроидом и каждой угловой точкой. Вы должны убедиться, что углы представлены так, что они варьируются между [0,360) градусов. Как только вы это получите, вы вроде углы затем используют полученный порядок для определения порядка точек.
изображение, которое вы представили, требует предварительной обработки, поэтому я могу начинай работать над этим. Я читаю изображение непосредственно из StackOverflow, затем я инвертирую изображение так, чтобы черная звезда стала белой. Мне также нужно удалить номера, поэтому я использую bwareaopen, чтобы удалить любые небольшие участки текста. После этого я выполняю обнаружения угол изображения через corner, а я QualityFactor до 0,3, чтобы я мог обнаружить 10 углов. Очень конкретно:
%// Read image from StackOverflow
im = rgb2gray(imread('http://i.stack.imgur.com/dpbpP.jpg'));
%// Threshold the image and area open it
im_thresh = im <= 100;
im_open = bwareaopen(im_thresh, 50);
%// Detect corner points
out = corner(im_open, 'QualityLevel', 0.3);
%// Show the image with the corner points
imshow(im_open);
hold on
plot(out(:,1), out(:,2), 'r.')
im_open содержится наше окончательное изображение. Этот вот что я получаю:

теперь давайте найдем центроид. Это можно просто сделать, найдя координаты ненулевых местоположений и найдя среднее значение каждого измерения:
[rows, cols] = find(im_open);
cenX = mean(cols);
cenY = mean(rows);
cenX и cenY содержат (x,y) расположение центроида изображения. Просто чтобы убедиться, что мы правильно:
imshow(im_open);
hold on;
plot(cenX, cenY, 'r.', 'MarkerSize', 18);
получаем:

очень приятно. Теперь,out в более ранний код содержит (x,y) точки угловых точек. Все, что вам нужно сделать, это определить угол от центроида до каждой угловой точки, а затем отсортировать углы. Вы бы использовали этот порядок сортировки, чтобы переставить угловые точки, чтобы дать вам ваши упорядоченные точки. Если вы хотите стрелки, вам нужно будет отсортировать значения в по возрастанию порядок. Если вы хотите против часовой стрелки, вам нужно будет отсортировать в спуск порядок. Я предоставьте это вам в том, что вы хотите решить, но я напишу код, который позволит вам сделать и то, и другое. Поэтому просто сделайте так:
%// Determine angles (in degrees)
angles = atan2d(out(:,2) - cenY, out(:,1) - cenX);
%// Any negative angles, add 360 degrees to convert to positive
angles(angles < 0) = 360 + angles(angles < 0);
%// Sort the angles
[~,ind] = sort(angles); %// clockwise
%[~,ind] = sort(angles, 'descend'); %// counter-clockwise
%// Re-arrange the corner points to respect the order
out_reorder = out(ind,:);
теперь последний тест, чтобы построить эти точки, а также построить номер рядом с каждой точкой, чтобы увидеть, если мы получили это право. Это можно сделать с помощью:
%// Show image
imshow(im_open);
hold on;
%// Show points
plot(out_reorder(:,1), out_reorder(:,2), 'r.', 'MarkerSize', 18);
%// Place a textbox at each point and show a sequence number
for idx = 1 : size(out_reorder,1)
text(out_reorder(idx,1), out_reorder(idx,2), num2str(idx), 'FontSize', 24, 'Color', 'green');
end
получаем:
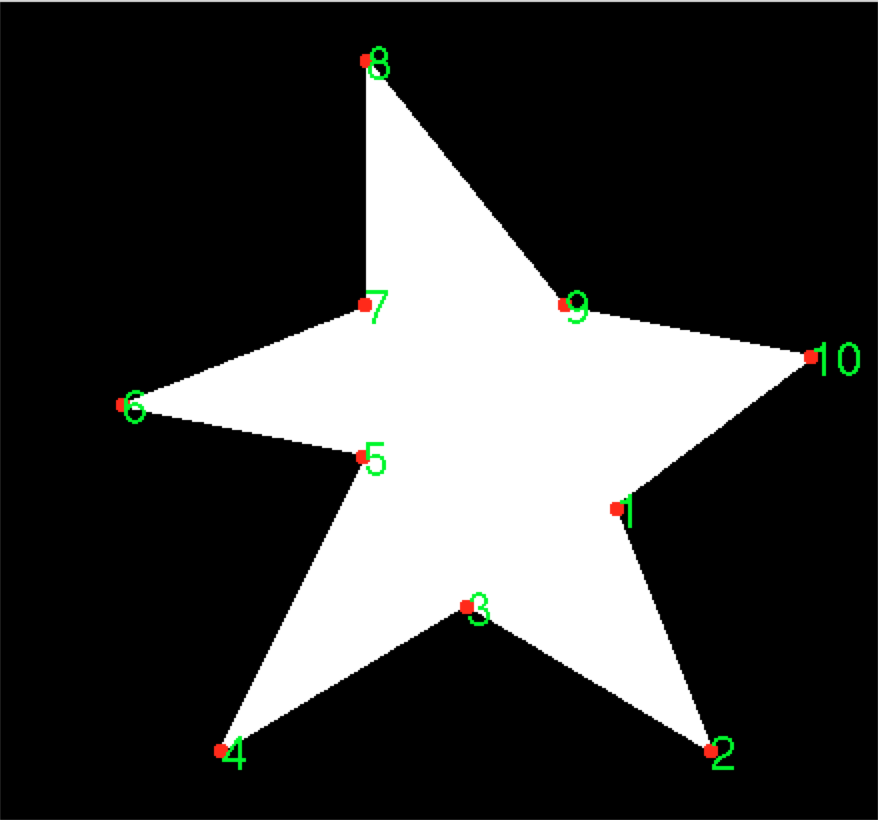
выглядит хорошо для меня! Как таковой,out_reorder дает вам угловые точки, чтобы они следовали либо по часовой стрелке, либо против часовой стрелки. Каждый ряд, который вы встречаете последовательно, дает вам следующую точку, которая естественно следует по часовой стрелке или против часовой стрелки, которую вы ищете.
Также обратите внимание, где начинается нумерация. Угол 0 определяется горизонтальной линией, которая указывает на восток относительно центроида. Таким образом, ближайшая точка к 0, как мы начинаем в порядке возрастания, где вы видите число 1. После 1, вы видите, что он метет по часовой стрелке пока не закончатся угловые точки.
