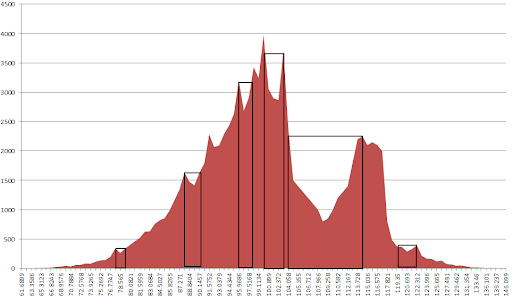
Определение локальных минимумов в гистограмме
Мне интересно найти локальные минимумы в гистограмме, которая примерно напоминает
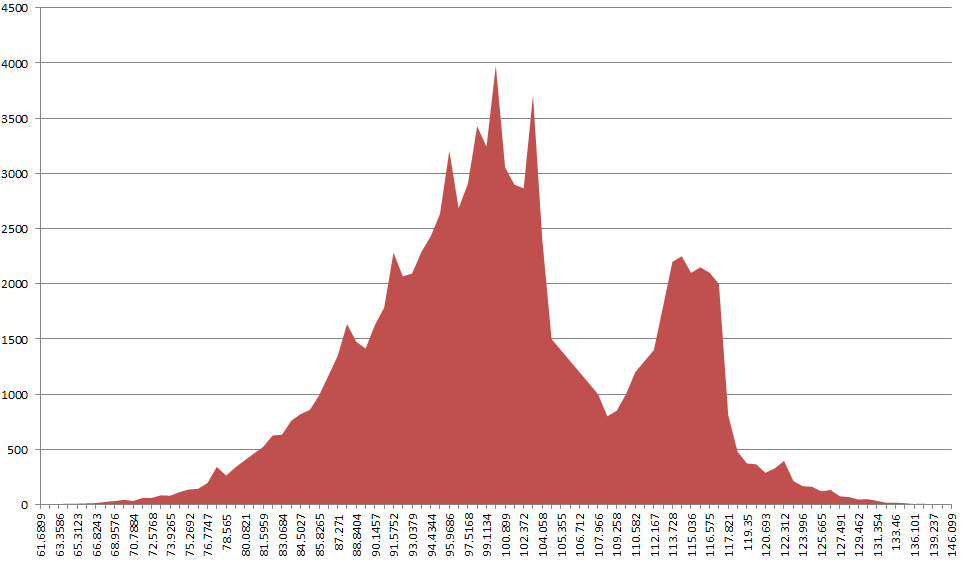
Я хотел бы найти локальный минимум в 109.258, и самый простой способ сделать это-определить, является ли количество отсчетов в 109.258 ниже среднего количества отсчетов в некотором интервале вокруг (и включая 109.258). Самое трудное для меня-определить этот интервал.
Что касается источника этих данных, это гистограмма с 100 бункерами неравномерной ширины. Каждая ячейка имеет значение (показано на оси x) и количество образцов, попадающих в эту ячейку (показано на оси y). Я пытаюсь найти "лучшее" место для разделения гистограммы. Каждая сторона раскола распространяется вниз по двоичному дереву как часть алгоритма классификации.
Я думаю, что моим лучшим курсом действий было бы попытаться подогнать кривую к этой гистограмме, используя что-то вроде Левенберга-Марквардта алгоритм а затем сравнить локальные минимумы, чтобы найти "лучший". Надлежащая мера " лучшего "будет включать некоторое указание на значимость этого разделения, которое измеряется как разница между средними подсчетами в интервале слева и средним подсчетом в интервале справа, а затем, возможно, вес каждой разницы с количеством подсчетов, включенных для получения составного измерения" лучшего", если это имеет смысл.
в любом случае, вычислительная сложность алгоритма не является огромной проблемой, 100 бункеров - это максимальное число, с которым я ожидал столкнуться. Однако этот расчет будет выполняться один раз для каждой выборки, поэтому сохранение его линейным по отношению к числу бункеров, конечно, было бы идеальным.
кстати, я делаю все на C++ и использую библиотеки boost и STL, поэтому в этом отношении нет ничего запретного.
любые мысли или идеи, касающиеся передовой практики, будут очень признателен!
4 ответов
Если я правильно понял kmore хочет разбить два "пика" на основе наибольшего разделения (произведение количества гистограмм и расстояния между ячейками). Если это правда:
- найти все maxs.
- для каждого максимального прямоугольника сборки, как на рис.
- найти прямоугольник с max белый, что дает вам диапазон x, чтобы найти желаемый bin 109.258
Levenberg-Marquardt не очень хороший выбор в пересеченной местности оптимизации - и ваш довольно прочный. Там много местных минимумов. Левенберг-Марквардт вполне может найти местный минимум около 100. Или он может найти один из двух глобальных минимумов в крайних точках графика, где функция завершается нулем.
вы хотите что-то, что находит наиболее значительный локальный минимум. Например, какой-то алгоритм кластеризации. Вот очень простой один:
Шаг 1: Найдите локальные экстремумы в наборе данных. Это экстремумы на экстремумах диапазона плюс внутренние локальные минимумы и максимумы. С вашей гистограммой у вас должно быть нечетное число таких экстремумов, чередующихся между минимумами и максимумами.
Шаг 2: Найти пару с наименьшей дельтой. Это будет либо (local max, local min), либо (local min, local max) пара.
Шаг 3: Найдите пару элементов для удаления, один из
- пара, найденная на Шаге 2
- пара, содержащая первый элемент пары из шага 2 и его предшественника
- пара, содержащая последний элемент пары из шага 2 и его преемника
когда найденная пара включает граничную точку, вы должны использовать Вариант 2 или 3, Если это необходимо. Для внутренней пары вы можете использовать некоторые эвристики при выборе между тремя вариантами. Или ты можешь просто ... простая вещь и используйте найденную пару.
Шаг 4: Удалите пару элементов из Шага 3, отслеживая удаленную пару.
Шаг 5: Повторите шаги с 2 по 4, пока в наборе данных extrema не останется только три элемента (экстремумы диапазона плюс локальный Макс, надеюсь, глобальный Макс).
последние удаленные минимумы-это то, что вы хотите.
существует множество других алгоритмов кластеризации. Я представил довольно сырой и явно не особенно быстро. Тот, который хорошо распространяется на гораздо больше данных, а более высокие размерные данные-это алгоритм максимизации ожиданий. Имитационный отжиг (Metropolis-Hastings) также может быть адаптирован к этой проблеме.
проблема, конечно, может быть преобразована в одну из пиковых находок путем функциональной манипуляции данными (инверсия или отрицание являются очевидными кандидатами).
в качестве альтернативы, если пример типичен, можно начать с поиска пиков в непереведенных данных и искать области, где пики (относительно) широко разделены как кандидаты для содержания хороших локальных минимумов.
Я всегда рекомендую метод, используемый ROOT TSpectrum классы для поиска пиков.
алгоритм подчиненного подробно обсуждается в
- М. Morhac и соавт.: методы исключения предпосылки для многомерных спектров гамма-излучения совпадения. ядерные инструменты и методы в физических исследованиях A 401 (1997) 113-132.
- М. Morhac и соавт.: эффективная одно - и двумерная деконволюция золота и ее применение для гамма-излучения разложение спектров. ядерные инструменты и методы в физических исследованиях A 401 (1997) 385-408.
- М. Morhac и соавт.: идентификация пиков в многомерных совпадающих гамма-спектрах. ядерные приборы и методы в исследовательской физике A 443(2000), 108-125.
копии этих документов хранятся на корневом веб-сайте и связаны в документации TSpectrum для тех, кто не имеет подписки на NIM A.
то, что вы хотите, кажется, сложнее, чем просто локальный минимум. Кроме того, концепция локального минимума сильно зависит от вашего выбора бункеров.
вы слышали о метод Отсу? Это может быть больше похоже на то, что вы хотите.
вот еще метод Отсу ссылка.