Оптимального алгоритма муравьиной колонии

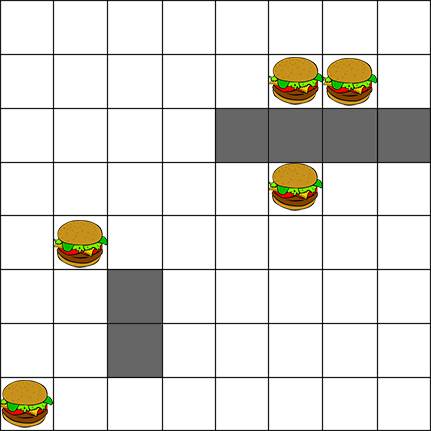
предположим, что существует сетка, содержащая обе стены (заблокированные ячейки), а также продукты питания, размещенные в любом месте сетки.

Image of example grid

теперь предположим, что мы пытаемся решить оптимальное место для размещения колонии муравьев на этой сетке, так что муравьи должны пройти наименьшее расстояние (в любом направлении к/от начальной точки колонии), чтобы получить максимальное количество пищи.

до сих пор лучший подход, который я придумал, это следующее:

for each square on the grid
    use a shortest path algorithm to find the distance to/from each food source from this square
    sum these distances to find a number and put the number in that square
select the square with the smallest number

будет ли этот подход работать? Есть ли более эффективное решение?

12
algorithm path-finding shortest-path

2 ответов

Да, ваш алгоритм работает, но вы можете оптимизировать его для случая, когда [количество продуктов] 

distances = new int[ROWS][COLS];

for each food-packet on the grid
    use a shortest path algorithm to find the distance to/from each square from this food-packet
    accumulate the distances for each square in the 'distances' array

в конце концов, массив расстояний будет содержать объем работы, которую колония муравьев должна сделать, чтобы захватить все пакеты с едой в сетке. Поместите колонию муравьев на квадрат, который имеет наименьшее значение.

но обратите внимание, что асимптотическая сложность этого подхода остается такой же, как и алгоритм, который вы дали в вопросе.


P. S Еще одна очевидная оптимизация вашего алгоритма была дана taoufiq в комментариях. то есть. прекратите вычислять любую сумму кратчайших путей, которая превышает кратчайшее расстояние, найденное до сих пор.

надеюсь, это было полезно.

2

некоторые оптимизации, основанные на подходе грубой силы:

  • следите за кратчайшим расстоянием и прекратите вычислять любые sum of shortest paths, что превышает

  • если расстояние Манхэттен (delta(x) + delta(y)) длиннее, чем когда-либо записанное короткое расстояние, прекратите вычислять

  • в сочетании с оптимизацией расстояния Манхэттена: начните с центра доски или центра пакетов с едой и работайте наизнанку. Оптимальное расположение, скорее всего, будет где-то посередине

  • уменьшите домен поиска до области между пакетами продуктов питания (т. е. от [1,1] to [6,7], а не [0,0] to [7,7])

  • Nikunj'оптимизация ы

далее, Если ваша доска действительно огромная, an оптимизация решателя возможно, удастся уменьшить количество вычислений. Тем не менее, ваша проблема кажется невыпуклой проблема, и многие решают проблемы решение.

0