Ориентированный на данные обход дерева без рекурсии
У меня есть древовидная структура: модель имеет корневой узел, и каждый узел имеет любое количество дочерних узлов, а также любое количество сеток.
много времени в моем приложении тратится на пересечение этого дерева и выполнение вычислений, таких как отбраковка разочарования и умножение матрицы. В настоящее время он наивно реализован, где каждый узел имеет векторы дочерних узлов и сеток, а дерево рекурсивно пересекается. Это очень медленно.
Я искал в ориентированном на данные дизайне, и мне нравится идея, что он очень дружелюбен к кэшу. Я думал о чем-то подобном:--2-->
struct Mesh
{
// misc data
MeshID mMeshID;
}
// probably needs more information?
struct Node
{
// begin and end index into Models 'mNodes'
uint32_t mChildrenBegin;
uint32_t mChildrenEnd;
// as above but for meshes
uint32_t mMeshesBegin;
uint32_t mMeshesEnd;
}
struct Model
{
std::vector<Node> mNodes;
std::vector<Mesh> mMeshes;
}
теперь мне нужно пересечь дерево, чтобы получить список видимых сеток. На каждом узле я должен проверить, виден ли узел. Следующие ветви:
- узел виден. Все дочерние узлы и сетки под ним также видны. Не углубляйся в эту ветвь. Проверьте другие узлы на той же глубине.
- узел не видимый. Никакие дочерние узлы или сетки на этом узле или под ним не будут видны. Не углубляйся в эту ветвь. Проверьте другие узлы на той же глубине.
- узел частично виден. Некоторые узлы и/или некоторые сетки видны. Нужно идти глубже в иерархию.
дерево статично. После загрузки модели в приложение дерево никогда не изменяется. Поэтому я должен как-то использовать эту информацию, чтобы получить эффективную структуру.
Я озадачен, как подойти к этому.
пара вопросов;
- как разместить узлы в памяти? Является ли корневым узлом первого индекса? Добавляются ли другие узлы на основе глубины?
- Как выполнить итерацию дерева без использования рекурсии? Я не хочу посещать каждый узел, если мне действительно не нужно. Например, если узел с глубиной=2 не виден, все его сетки и дочерние элементы (и их сетки) не должны тестироваться, а пропускаться полностью.
3 ответов
вы можете представить дерево как один массив в памяти в глубину-первый порядок обхода
struct Node {
... node data ...
int next;
};
std::vector<Node> nodes;
next поле сохраняет индекс следующего узла на том же или более высоком уровне; первые дочерние элементы узла явно не указаны, поскольку это узел, следующий за текущим узлом в последовательности (если next также не указывает на него; в этом случае текущий узел не имеет дочерних элементов).
Например в дереве:
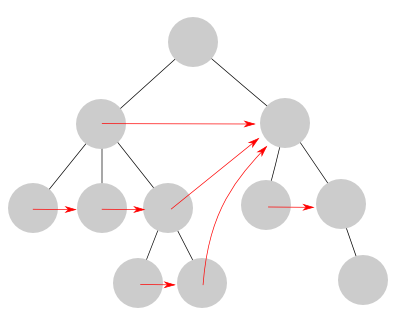
красные стрелки показывают, где next указывает на.
обход, например, для рендеринга становится:
void check(int ix) {
switch(nodes[ix].visibility()) {
case VISIBLE:
// Draw whole subtree, no more checking needed
for (int i=ix,e=nodes[ix].next; i!=e; i++) {
nodes[i].draw();
}
break;
case PARTIALLY_VISIBLE:
nodes[ix].draw();
for (int c=ix+1, e=nodes[ix].next; c!=e; c=nodes[c].next) {
check(c);
}
break;
}
}
тот же код также может быть преобразован в нерекурсивный, сохраняя явный стек (не уверен, почему это было бы хорошей идеей, если операция узла и проверка не очень быстры или дерево безумно глубоко).
короткая версия: используйте ответ предварительного заказа 6502 вместо. Я оставлю свой предыдущий ответ ниже, потому что у него все еще есть интересный код и комментарии.
выложите свой массив хранения в полу-предзаказе. То есть: конечный узел стража, корни, дети первого корня, дети первого корня, дети первого внука первого корня и так далее. Затем пересечь дерево с помощью рекурсивного обхода полу-предварительного порядка, который сохраняет копии индексной информации direct предки и их братья и сестры в стопке. Таким образом, ваш обход будет сканировать массив хранения слева направо без возвратов. Вам не нужно посещать все узлы с рекурсией, и любой пропуск поддеревьев, который вы делаете, будет только прыгать вперед в массиве хранения.
model.semiPreOrderTraversalRecur(model.getEnd()); // traverse the whole tree
...
// NOTE: pass prnt by *COPY* -- break Node into index portion and app. data portion; we only need the index portions here
void Model::semiPreOrderTraversalRecur(Node prnt)
{
Node children[prnt.mChildrenEnd - prnt.mChildrenBegin]; // just index info
uint32_t i;
// visit children of prnt; determine visibility etc.
for (i = prnt.mChildrenBegin; i < prnt.mChildrenEnd; ++i)
{
cout << "Visiting " << mNodes[i].mVal << endl;
mNodes[i].mInvisible = false; // TODO: determine based on culling, etc.
children[i - prnt.mChildrenBegin] = mNodes[i]; // just index info
}
// recurse on children as necessary
for (i = 0; i < prnt.mChildrenEnd - prnt.mChildrenBegin; ++i)
if (!children[i].mInvisible && children[i].mChildrenBegin != children[i].mChildrenEnd)
semiPreOrderTraversalRecur(children[i]);
}
длинная версия (некоторые из них устранены): я думаю, вы можете достичь того, что хотите, добавив немного больше информации в свою структуру узлов: индекс родительского узла и индекс текущего узла. (Последнее может быть не совсем необходимо, поскольку оно, вероятно, может быть получено из указателя на узел и вектор хранения узла.)
Это должно дать вам достаточно контекстуальной информации, чтобы легко перемещать "вверх", "вниз" или "вбок" к родному брату, как вы хотите, учитывая любой узел в дереве. Чтобы перейти "вверх", вы просто переходите к родительскому индексу. Чтобы перейти вниз, перейдите к любому из дочерних индексов. Чтобы переместить" боком " к родному брату, вы просто увеличиваете / уменьшаете ток Индекс узла (после проверки того, что вы не последний/первый ребенок вашего родителя).
вы можете рассмотреть возможность объединения структур узлов и сеток, чтобы вы могли хранить их смежно в одном векторе. Производительность кэша, которая хороша для гусыни, обычно хороша для Гусака. Поскольку ваша сетка хранится в другом векторе, они, вероятно, находятся далеко в памяти от своих братьев-узлов, и доступ к ним в середине обхода будет оказывать большее давление на кэш. Конечно, если ваш У Mesh гораздо больше данных, чем у вашего узла (или наоборот), или вам не нужно посещать Mesh во время обхода, тогда это может быть не очень хороший вариант, поскольку он будет тратить память. Кроме того, вашей сетке, вероятно, не нужны все индексы дерева, поскольку они являются терминальными узлами и могут быть специальными, когда вы посещаете дочерние узлы узла. В зависимости от деталей, ваше первоначальное предложение для хранить сетка отдельно может быть главно.
в коде ниже я объединяю ваш узел и сетку структуры и хранить их в одном векторе.
#include <cstdint>
#include <iostream>
#include <vector>
#include <string>
#include <chrono>
#include <thread>
using namespace std;
struct Node
{
uint32_t mParentIndex; // index of parent Node in Model
uint32_t mIndex; // index of this Node in Model (may be possible to derive this from Node pointer and Model's vector rather than storing it)
uint32_t mChildrenBegin; // begin and end index of children Node in Model
uint32_t mChildrenEnd;
bool mInvisible; // used during semiPreOrderTraversal to remember no need to traverse subtree rooted at this Node
int mVal; // dummy data for debugging
};
struct Model
{
vector<Node> mNodes; // preferably private, but your call
Model(istream *in = NULL);
Node *getEnd(void) { return &mNodes[0]; } // sentinel end node that always exists and has itself as parent
Node *getRoot(void) { return getChild(getEnd()); }
Node *getParent(Node *curr) { return &mNodes[curr->mParentIndex]; } // always safe to call; returns end as sentinel
Node *getNextSibling(Node *curr) { Node *prnt = getParent(curr); return (curr->mIndex && curr->mIndex + 1 < prnt->mChildrenEnd ? &mNodes[curr->mIndex + 1] : NULL); }
Node *getPrevSibling(Node *curr) { Node *prnt = getParent(curr); return (curr->mIndex > prnt->mChildrenBegin ? &mNodes[curr->mIndex - 1] : NULL); }
Node *getChild(Node *curr, unsigned nth_child = 0) { unsigned index = curr->mChildrenBegin + nth_child; return (index < curr->mChildrenEnd ? &mNodes[index] : NULL); }
void semiPreOrderTraversal(void);
void semiPreOrderTraversalRecur(Node prnt);
private:
int buildFromStreamRecur(Node *curr, int val, istream &in);
};
void Model::semiPreOrderTraversal(void)
{
Node *curr = getRoot();
Node *next;
cout << "Beginning Semi-Pre-Order traversal of tree!" << endl;
if (NULL == curr)
goto DONE;
while (1)
{
// TODO: visit curr; determine and record mInvisible in curr
cout << "Visiting " << curr->mVal << endl;
curr->mInvisible = false;
// try to move to sibling
if (NULL == (next = getNextSibling(curr)))
{
// try to move to children of siblings
curr = getChild(getParent(curr)); // move back to oldest sibling
cout << "No more siblings to visit! Try to visit their children. Rewinding to oldest sibling " << curr->mVal << endl;
while (curr->mInvisible || NULL == (next = getChild(curr)))
{
cout << "No children to visit of " << curr->mVal << endl;
// shouldn't visit curr's children or it has no children
// try to move to sibling
if (NULL == (next = getNextSibling(curr)))
{
cout << "Reached end of siblings again -> completed traversal of subtree rooted by parent " << getParent(curr)->mVal << endl;
// ascend while we can't find a uncle to check for children to visit
do {
if (getEnd() == (curr = getParent(curr)))
goto DONE; // got back to end -> traversal complete
cout << "Moved back up to " << curr->mVal << endl;
} while (NULL == (next = getNextSibling(curr)));
cout << "Found a great^Nth uncle (" << next->mVal << ") to check for children to visit!" << endl;
}
// else check sibling for children to visit
curr = next;
cout << "Trying to visit children of " << curr->mVal << endl;
}
// visit children of curr
cout << "Will visit children of " << curr->mVal << endl;
}
else
cout << "Will visit sibling of " << curr->mVal << endl;
curr = next;
}
DONE:
cout << "Finished Semi-Pre-Order traversal of tree!" << endl;
}
void Model::semiPreOrderTraversalRecur(Node prnt)
{
Node children[prnt.mChildrenEnd - prnt.mChildrenBegin]; // just index info
uint32_t i;
// visit children of prnt; determine visibility etc.
for (i = prnt.mChildrenBegin; i < prnt.mChildrenEnd; ++i)
{
cout << "Visiting " << mNodes[i].mVal << endl;
mNodes[i].mInvisible = false;
children[i - prnt.mChildrenBegin] = mNodes[i]; // just index info
}
// recurse on children as necessary
for (i = 0; i < prnt.mChildrenEnd - prnt.mChildrenBegin; ++i)
if (!children[i].mInvisible && children[i].mChildrenBegin != children[i].mChildrenEnd)
semiPreOrderTraversalRecur(children[i]);
}
Model::Model(istream *in)
{
Node dmy, *end;
mNodes.push_back(dmy); // create sentinel end node
end = getEnd();
end->mParentIndex = 0;
end->mIndex = 0;
end->mChildrenBegin = 1;
end->mChildrenEnd = 1;
end->mVal = -1;
if (in)
buildFromStreamRecur(getEnd(), 0, *in);
}
int Model::buildFromStreamRecur(Node *curr, int val, istream &in)
{
uint32_t numChildren, i, currInd = curr->mIndex;
// read in how many children curr will have
in >> numChildren;
// allocate children in mNodes and set curr's children references
// NOTE: protect against reallocations of mNodes
curr->mChildrenBegin = mNodes.size();
for (i = 0; i < numChildren; ++i)
{
Node node;
node.mParentIndex = currInd;
node.mIndex = mNodes.size();
node.mChildrenBegin = (uint32_t) -1;
node.mChildrenEnd = (uint32_t) -1;
node.mVal = val++;
mNodes.push_back(node);
}
curr = &mNodes[currInd];
curr->mChildrenEnd = mNodes.size();
cout << "Node " << curr->mVal << " is complete! mParentIndex = " << curr->mParentIndex << "; mIndex = " << curr->mIndex
<< "; mChildrenBegin = " << curr->mChildrenBegin << "; mChildrenEnd = " << curr->mChildrenEnd << endl;
// recursively build children
// NOTE: protect against reallocations of mNodes
for (i = 0; i < numChildren; ++i)
{
curr = &mNodes[currInd];
curr = &mNodes[curr->mChildrenBegin + i];
val = buildFromStreamRecur(curr, val, in);
}
return val;
}
int main(int argc, char **argv)
{
Model m(&cin);
m.semiPreOrderTraversal();
m.semiPreOrderTraversalRecur(*m.getEnd());
return 0;
}
нерекурсивный, предварительный обход всего дерева будет выглядеть примерно так:
Node *curr = model.getRoot(); // TODO: handle empty tree
Node *next;
bool shouldnt_visit_children;
while (1)
{
// TODO: visit curr -- determine shouldnt_visit_children
if (shouldnt_visit_children || NULL == (next = model.getChild(curr)))
{
// move to next sibling; if no siblings remain then ascend while no siblings remain
while (NULL == (next = model.getNextSibling(curr)))
if (model.getEnd() == (curr = model.getParent(curr)))
goto DONE;
curr = next;
}
else
curr = next; // descend to first child
}
DONE:;
все это, как говорится, я не вижу никаких ярко очевидных причин, почему такая реализация (в отличие от связанной структуры, как вы ранее), вероятно, будет иметь гораздо лучшую производительность кэша. Как векторы выкладываются и как вы получаете к ним доступ, это то, что будет управлять вашей производительностью кэша. Несмотря на это, я не вижу никаких убедительных причин, по которым вы не можете достичь аналогичного результата, создавая связанное дерево аналогичным образом. Например, если вы обнаружите/считаете, что выкладываете свои векторы в полу-предварительном порядке вида обхода дерева (т. е.-вектор выкладывается как: конец, корень, дети корня, дети первого ребенка корня, дети первого внука корня и т. д.) дает оптимальную производительность кэша для вашего приложения, то весьма вероятно, что построение связанного дерева с использованием того же полу-предварительного порядка сборки даст аналогичные результаты, так как ваш распределитель памяти, вероятно, упакует ваше дерево в память таким же образом, как вы это сделали бы явно. Конечно, при вашем подходе вы можете контролировать это с уверенностью, а не в зависимости от ваших структур и связанных распределителей.
явное управление макетом вашего узла и сетки в памяти может дать вам лучшую производительность кэша, как вы можете "заставьте" его плотно упаковать ваши объекты в память и применить тип шаблона доступа / локальности, который вы предпочитаете, но приличный распределитель, вероятно, достигнет аналогичного результата, особенно если построение дерева выполняется только один раз при запуске.
если вы в основном делаете предзаказ траверсы, как ваши вопросы, кажется, предлагают, то я бы рекомендовал выложить вектор хранения в полу-предзаказе, как я выше описал: конец, корень, дети корня, дети первого ребенка корня, корни дети первого внука и так далее.
PS-Если ваши обхода всегда начинаются с корня, то вы можете устранить mParentIndex в узле тоже и вместо этого построить явный стек предков, когда вы идете по дереву, чтобы позволить вам пройти обратно вверх по дереву после спуска (это, вероятно, то, что рекурсия сделала неявно). Если вам нужно иметь возможность перемещаться по дереву из любого случайного заданного узла, вам нужно сохранить индекс вашего родителя в Узел.
EDIT: как я уже упоминал в одном из моих комментариев, предложенный мной макет полу-предварительного порядка также имеет свойство, что все потомки сетки узла могут быть представлены в простом числовом диапазоне [Node.mDescedantMeshBegin, Node.mDescendantMeshEnd), когда вы храните сетку отдельно, как предложено. Таким образом, если вам нужно или хотите создать явный список видимых сеток, пересекая дерево, то всякий раз, когда вы найдете видимый узел, вы можете легко включить весь этот диапазон видимой сетки потомков в ваш список очень легко.
EDIT2: я значительно обновил код. Я добавил построитель рекурсивной модели на основе входного потока полу-предварительного заказа. Я исправил некоторые ошибки. Самое главное, я добавил функцию, которая выполняет нерекурсивный, полу-предварительный обход модели. Это не так просто, как настоящий предзаказ, но это может вас заинтересовать. Рекурсивная версия может быть намного проще - я подумаю о добавляю это. В моем тестировании посещение узлов происходит очень хорошо слева направо в mNodes. Тем не менее, доступ к памяти иногда идет назад в массиве хранения, когда мы поднимаемся вверх по дереву. Я считаю, что эти обратные ссылки могут быть удалены путем поддержания явного массива копии предков (по крайней мере, их индексной информации) в стеке во время обхода. Функциональность вызовов, таких как getParent () и getNextSibling (), должна быть переписана на используйте этот массив вместо того, чтобы прыгать в самом векторе хранения, но это можно сделать. Тогда ваши обращения к памяти mNodes будут скользить только слева направо, что, вероятно, близко к оптимальному для производительности кэша (при условии, что ваше дерево достаточно мелкое, чтобы ваши предки в стеке всегда были в кэше и не создавали чрезмерного давления кэша).
EDIT3: я добавил рекурсивный полу-предварительный обход порядка, и он тривиален по сравнению с итеративным версия. Также до смешного легко передать копии индексных частей ваших узлов, чтобы сохранить их в стеке, чтобы при развертывании рекурсии вы фактически не возвращались и не получали доступ к более ранним частям вашего массива хранения. Вместо этого вы просто смотрите на то, что находится в стеке, который почти наверняка будет в кэше-предполагая, что ваши деревья не очень глубокие+широкие. Вы должны хранить копии всех детей на заданном уровне. Недостаточно хранить только своих прямых предков, вы также должны хранить своих братьев и сестер. С помощью этого кода и выкладки вектора хранения в полу-предварительном порядке, все ваши обращения к памяти в обходе будет сканировать слева направо по массиву хранения без обратного отслеживания. Я думаю, у вас будет почти оптимальная производительность кэша. Я не вижу, как это может быть лучше.
входной сигнал образца.txt: каждое число представляет, сколько дочерних элементов имеет неявный текущий узел в предварительном порядке. В приведенном ниже, конечный узел sentinel имеет только 1 дочерний, a единственный корень (код поддерживает несколько корней, если вы хотите), корень имеет 5 детей, первый ребенок корня имеет 0 детей, второй ребенок корня имеет 2 детей и так далее. Я использовал интервал, чтобы указать структуру дерева глаз, но это не обязательно для самой программы.
1
5
0
2
7
0
0
0
1
0
0
0
0
2
1
0
0
1
0
4
1
0
2
1
0
1
0
0
0
0
пример вывода:
john-schultzs-macbook-pro:~ jschultz$ clear; ./a.out < input.txt
Node -1 is complete! mParentIndex = 0; mIndex = 0; mChildrenBegin = 1; mChildrenEnd = 2
Node 0 is complete! mParentIndex = 0; mIndex = 1; mChildrenBegin = 2; mChildrenEnd = 7
Node 1 is complete! mParentIndex = 1; mIndex = 2; mChildrenBegin = 7; mChildrenEnd = 7
Node 2 is complete! mParentIndex = 1; mIndex = 3; mChildrenBegin = 7; mChildrenEnd = 9
Node 6 is complete! mParentIndex = 3; mIndex = 7; mChildrenBegin = 9; mChildrenEnd = 16
Node 8 is complete! mParentIndex = 7; mIndex = 9; mChildrenBegin = 16; mChildrenEnd = 16
Node 9 is complete! mParentIndex = 7; mIndex = 10; mChildrenBegin = 16; mChildrenEnd = 16
Node 10 is complete! mParentIndex = 7; mIndex = 11; mChildrenBegin = 16; mChildrenEnd = 16
Node 11 is complete! mParentIndex = 7; mIndex = 12; mChildrenBegin = 16; mChildrenEnd = 17
Node 15 is complete! mParentIndex = 12; mIndex = 16; mChildrenBegin = 17; mChildrenEnd = 17
Node 12 is complete! mParentIndex = 7; mIndex = 13; mChildrenBegin = 17; mChildrenEnd = 17
Node 13 is complete! mParentIndex = 7; mIndex = 14; mChildrenBegin = 17; mChildrenEnd = 17
Node 14 is complete! mParentIndex = 7; mIndex = 15; mChildrenBegin = 17; mChildrenEnd = 17
Node 7 is complete! mParentIndex = 3; mIndex = 8; mChildrenBegin = 17; mChildrenEnd = 19
Node 16 is complete! mParentIndex = 8; mIndex = 17; mChildrenBegin = 19; mChildrenEnd = 20
Node 18 is complete! mParentIndex = 17; mIndex = 19; mChildrenBegin = 20; mChildrenEnd = 20
Node 17 is complete! mParentIndex = 8; mIndex = 18; mChildrenBegin = 20; mChildrenEnd = 20
Node 3 is complete! mParentIndex = 1; mIndex = 4; mChildrenBegin = 20; mChildrenEnd = 21
Node 19 is complete! mParentIndex = 4; mIndex = 20; mChildrenBegin = 21; mChildrenEnd = 21
Node 4 is complete! mParentIndex = 1; mIndex = 5; mChildrenBegin = 21; mChildrenEnd = 25
Node 20 is complete! mParentIndex = 5; mIndex = 21; mChildrenBegin = 25; mChildrenEnd = 26
Node 24 is complete! mParentIndex = 21; mIndex = 25; mChildrenBegin = 26; mChildrenEnd = 26
Node 21 is complete! mParentIndex = 5; mIndex = 22; mChildrenBegin = 26; mChildrenEnd = 28
Node 25 is complete! mParentIndex = 22; mIndex = 26; mChildrenBegin = 28; mChildrenEnd = 29
Node 27 is complete! mParentIndex = 26; mIndex = 28; mChildrenBegin = 29; mChildrenEnd = 29
Node 26 is complete! mParentIndex = 22; mIndex = 27; mChildrenBegin = 29; mChildrenEnd = 30
Node 28 is complete! mParentIndex = 27; mIndex = 29; mChildrenBegin = 30; mChildrenEnd = 30
Node 22 is complete! mParentIndex = 5; mIndex = 23; mChildrenBegin = 30; mChildrenEnd = 30
Node 23 is complete! mParentIndex = 5; mIndex = 24; mChildrenBegin = 30; mChildrenEnd = 30
Node 5 is complete! mParentIndex = 1; mIndex = 6; mChildrenBegin = 30; mChildrenEnd = 30
Beginning Semi-Pre-Order traversal of tree!
Visiting 0
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 0
Will visit children of 0
Visiting 1
Will visit sibling of 1
Visiting 2
Will visit sibling of 2
Visiting 3
Will visit sibling of 3
Visiting 4
Will visit sibling of 4
Visiting 5
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 1
No children to visit of 1
Trying to visit children of 2
Will visit children of 2
Visiting 6
Will visit sibling of 6
Visiting 7
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 6
Will visit children of 6
Visiting 8
Will visit sibling of 8
Visiting 9
Will visit sibling of 9
Visiting 10
Will visit sibling of 10
Visiting 11
Will visit sibling of 11
Visiting 12
Will visit sibling of 12
Visiting 13
Will visit sibling of 13
Visiting 14
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 8
No children to visit of 8
Trying to visit children of 9
No children to visit of 9
Trying to visit children of 10
No children to visit of 10
Trying to visit children of 11
Will visit children of 11
Visiting 15
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 15
No children to visit of 15
Reached end of siblings again -> completed traversal of tree rooted by parent 11
Moved back up to 11
Found a great^Nth uncle (12) to check for children to visit!
Trying to visit children of 12
No children to visit of 12
Trying to visit children of 13
No children to visit of 13
Trying to visit children of 14
No children to visit of 14
Reached end of siblings again -> completed traversal of tree rooted by parent 6
Moved back up to 6
Found a great^Nth uncle (7) to check for children to visit!
Trying to visit children of 7
Will visit children of 7
Visiting 16
Will visit sibling of 16
Visiting 17
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 16
Will visit children of 16
Visiting 18
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 18
No children to visit of 18
Reached end of siblings again -> completed traversal of tree rooted by parent 16
Moved back up to 16
Found a great^Nth uncle (17) to check for children to visit!
Trying to visit children of 17
No children to visit of 17
Reached end of siblings again -> completed traversal of tree rooted by parent 7
Moved back up to 7
Moved back up to 2
Found a great^Nth uncle (3) to check for children to visit!
Trying to visit children of 3
Will visit children of 3
Visiting 19
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 19
No children to visit of 19
Reached end of siblings again -> completed traversal of tree rooted by parent 3
Moved back up to 3
Found a great^Nth uncle (4) to check for children to visit!
Trying to visit children of 4
Will visit children of 4
Visiting 20
Will visit sibling of 20
Visiting 21
Will visit sibling of 21
Visiting 22
Will visit sibling of 22
Visiting 23
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 20
Will visit children of 20
Visiting 24
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 24
No children to visit of 24
Reached end of siblings again -> completed traversal of tree rooted by parent 20
Moved back up to 20
Found a great^Nth uncle (21) to check for children to visit!
Trying to visit children of 21
Will visit children of 21
Visiting 25
Will visit sibling of 25
Visiting 26
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 25
Will visit children of 25
Visiting 27
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 27
No children to visit of 27
Reached end of siblings again -> completed traversal of tree rooted by parent 25
Moved back up to 25
Found a great^Nth uncle (26) to check for children to visit!
Trying to visit children of 26
Will visit children of 26
Visiting 28
No more siblings to visit! Try to visit their children. Rewinding to oldest sibling 28
No children to visit of 28
Reached end of siblings again -> completed traversal of tree rooted by parent 26
Moved back up to 26
Moved back up to 21
Found a great^Nth uncle (22) to check for children to visit!
Trying to visit children of 22
No children to visit of 22
Trying to visit children of 23
No children to visit of 23
Reached end of siblings again -> completed traversal of tree rooted by parent 4
Moved back up to 4
Found a great^Nth uncle (5) to check for children to visit!
Trying to visit children of 5
No children to visit of 5
Reached end of siblings again -> completed traversal of tree rooted by parent 0
Moved back up to 0
Finished Semi-Pre-Order traversal of tree!
я реализовал еще не полностью совместимую версию XPath для Qt, которая, таким образом, включает в себя способы прохождения дерева узлов без необходимости использования рекурсивных функций. Существует копия одного из соответствующих разделов с использованием алгоритма для прохождения всех потомков данного узла (и в конечном итоге включая Self).
Если вы хотите увидеть реализация (вокруг линии 5480), оно доступен в SourceForge.net git repository. Этот последний теперь в github.
case AXIS_DESCENDANT:
case AXIS_DESCENDANT_OR_SELF:
switch(node_type)
{
case NODE_TYPE_NODE:
case NODE_TYPE_ELEMENT:
{
// as far as I know the type node is considered to be
// the same as elements (at least in XPath 1.0)
QDomNode node(context_node);
if(axis == AXIS_DESCENDANT_OR_SELF
&& (local_part.isEmpty() || local_part == context_node.toElement().tagName())
&& (any_prefix || prefix == context_node.prefix()))
{
result.push_back(context_node);
}
while(!node.isNull())
{
QDomNode next(node.firstChild());
if(next.isNull())
{
next = node;
while(!next.isNull()) // this should never happend since we should bump in context_node first
{
if(next == context_node)
{
// break 2;
goto axis_descendant_done;
}
QDomNode parent(next.parentNode());
next = next.nextSibling();
if(!next.isNull())
{
break;
}
next = parent;
}
}
// the local_part & prefix must match for us to keep the node
node = next;
if((local_part.isEmpty() || local_part == node.toElement().tagName())
&& (any_prefix || prefix == node.prefix()))
{
// push so nodes stay in document order
result.push_back(node);
}
}
axis_descendant_done:;
}
break;
default:
throw QDomXPathException_NotImplemented(QString("this axis (%1) does not support this node type (%2)").arg(static_cast<int>(axis)).arg(static_cast<int>(node_type)).toStdString());
}
break;
