Отдельная смесь гауссов в Python

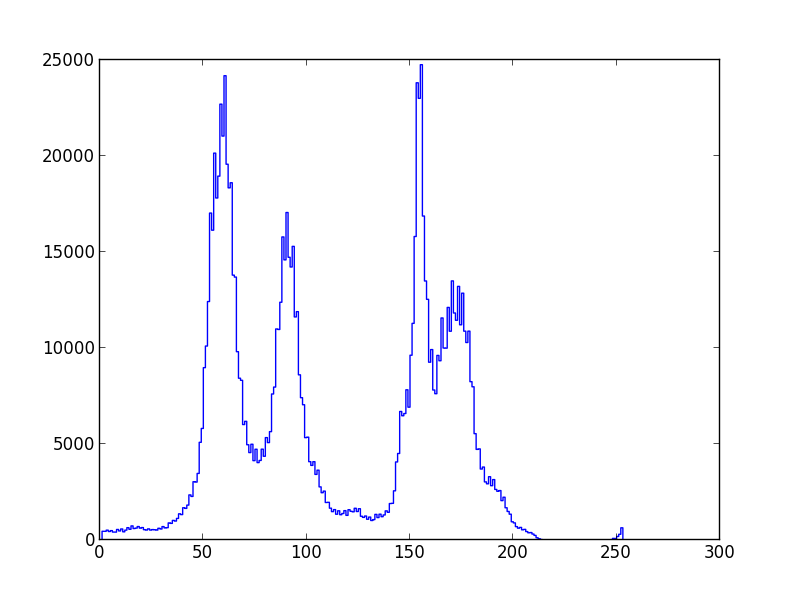
есть результат некоторого физического эксперимента, который можно представить в виде гистограммы [i, amount_of(i)]. Я полагаю, что результат может быть оценен смесью 4 - 6 гауссовых функций.

есть ли пакет в Python, который принимает гистограмму в качестве входных данных и возвращает среднее значение и дисперсию каждого гауссова распределения в распределении смеси?

исходные данные, например:

Sample data

8
normal-distribution python statistics

1 ответов

это смесь гауссов, и может быть оценено с помощью максимизации ожидания подход (в основном, он находит центры и средства распределения одновременно с оценкой того, как они смешиваются).

это реализовано в PyMix пакета. Ниже я создаю пример смеси нормалей и использую PyMix для подгонки к ним модели смеси, включая выяснение того, что вас интересует in, который является размером субпопуляций:

# requires numpy and PyMix (matplotlib is just for making a histogram)
import random
import numpy as np
from matplotlib import pyplot as plt
import mixture

random.seed(010713)  # to make it reproducible

# create a mixture of normals:
#  1000 from N(0, 1)
#  2000 from N(6, 2)
mix = np.concatenate([np.random.normal(0, 1, [1000]),
                      np.random.normal(6, 2, [2000])])

# histogram:
plt.hist(mix, bins=20)
plt.savefig("mixture.pdf")

все, что делает приведенный выше код, - это создание и построение смеси. Выглядит это так:

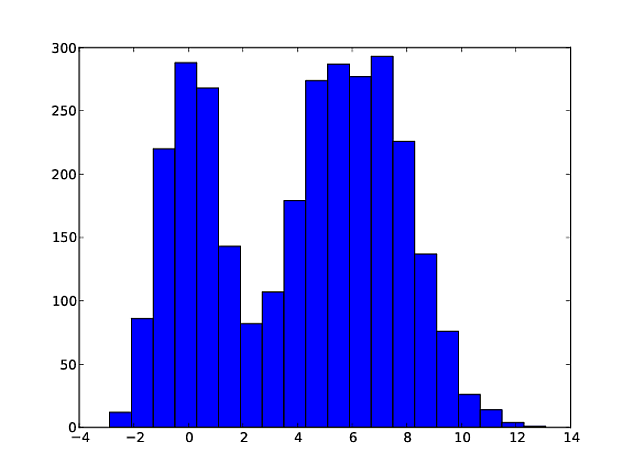
enter image description here

теперь фактически использовать PyMix, чтобы выяснить, каковы проценты:

data = mixture.DataSet()
data.fromArray(mix)

# start them off with something arbitrary (probably based on a guess from the figure)
n1 = mixture.NormalDistribution(-1,1)
n2 = mixture.NormalDistribution(1,1)
m = mixture.MixtureModel(2,[0.5,0.5], [n1,n2])

# perform expectation maximization
m.EM(data, 40, .1)
print m

выходная модель этого:

G = 2
p = 1
pi =[ 0.33307859  0.66692141]
compFix = [0, 0]
Component 0:
  ProductDist: 
  Normal:  [0.0360178848449, 1.03018725918]

Component 1:
  ProductDist: 
  Normal:  [5.86848468319, 2.0158608802]

обратите внимание, что он нашел двух нормалей совершенно правильно (один N(0, 1) и N(6, 2), примерно). Он также оценил pi, который является частью в каждый из двух дистрибутивов (вы упоминаете в комментариях, что это то, что вас больше всего интересует). У нас было 1000 в первом дистрибутиве и 2000 во втором дистрибутиве, и он получает деление почти ровно правильно: [ 0.33307859 0.66692141]. Если вы хотите получить это значение напрямую, делать m.pi.

несколько замечаний:

  • этот подход принимает вектор значений, а не гистограммы. Должно быть легко преобразовать ваши данные в вектор 1D (т. е. повернуть [(1.4, 2), (2.6, 3)] на [1.4, 1.4, 2.6, 2.6, 2.6])
  • мы должны были угадать количество гауссовых распределений заранее (он не будет вычислять смесь 4, Если вы попросите смесь 2).
  • нам пришлось ввести некоторые начальные оценки для распределений. Если вы делаете даже отдаленно разумные предположения, они должны сходиться к правильным оценкам.
11