Отношение Сигмы к полосе пропускания в гауссовом фильтре и гауссовском kde

применение функций scipy.ndimage.фильтры.gaussian_filter и scipy.статистика.gaussian_kde по заданному набору данных может дать очень похожие результаты, если sigma и bw_method параметры в каждой функции соответственно выбраны адекватно.

например, я могу получить для случайного 2D-распределения точек следующие графики, установив sigma=2. на gaussian_filter (левый участок) и bw_method=sigma/30. на gaussian_kde (справа сюжет):

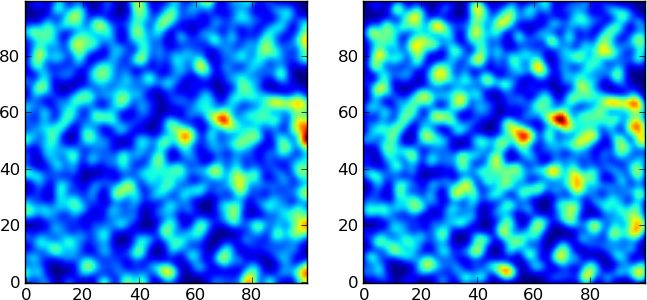
(MWE находится в нижней части вопроса)

очевидно, что существует связь между этими параметрами, поскольку один применяет гауссов фильтр, а другой-оценку плотности ядра Гаусса на данных.

определение каждого параметра:

• scipy.ndimage.фильтры.gaussian_filter, sigma:

Сигма: скалярная или последовательность скалярное стандартное отклонение для Гаусса ядро. Приведены стандартные отклонения гауссова фильтра для каждая ось как последовательность или как одно число, и в этом случае это равны для всех осей.

это я могу понять, учитывая определение гауссовского оператора:

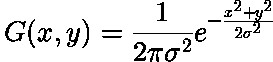
• scipy.статистика.gaussian_kde, bw_method:

bw_method: str, скалярный или вызываемый, опционный метод вычислите пропускную способность оценщика. Это может быть "Скотт", "Сильверман", а скалярная константа или вызываемая. Если скаляр, это будет использоваться напрямую как kde.факторный. Если вызываемый, он должен взять экземпляр gaussian_kde как только параметр и возвращает скаляр. Если None (по умолчанию),’ scott используемый. Дополнительные сведения см. В примечаниях.

в этом случае предположим, что вход для bw_method является скалярным (float), чтобы быть сопоставимым с sigma. Это место где я теряюсь, так как я не могу найти никакой информации об этом kde.factor параметр в любом месте.

что я хотел бы знать, это точное математическое уравнение который соединяет оба этих параметра (т. е.:sigma и bw_method когда используется поплавок), если это возможно.

MWE:

import numpy as np
from scipy.stats import gaussian_kde
from scipy.ndimage.filters import gaussian_filter
import matplotlib.pyplot as plt

def rand_data():
    return np.random.uniform(low=1., high=200., size=(1000,))

# Generate 2D data.
x_data, y_data = rand_data(), rand_data()
xmin, xmax = min(x_data), max(x_data)
ymin, ymax = min(y_data), max(y_data)

# Define grid density.
gd = 100
# Define bandwidth
bw = 2.

# Using gaussian_filter
# Obtain 2D histogram.
rang = [[xmin, xmax], [ymin, ymax]]
binsxy = [gd, gd]
hist1, xedges, yedges = np.histogram2d(x_data, y_data, range=rang, bins=binsxy)
# Gaussian filtered histogram.
h_g = gaussian_filter(hist1, bw)

# Using gaussian_kde
values = np.vstack([x_data, y_data])
# Data 2D kernel density estimate.
kernel = gaussian_kde(values, bw_method=bw / 30.)
# Define x,y grid.
gd_c = complex(0, gd)
x, y = np.mgrid[xmin:xmax:gd_c, ymin:ymax:gd_c]
positions = np.vstack([x.ravel(), y.ravel()])
# Evaluate KDE.
z = kernel(positions)
# Re-shape for plotting
z = z.reshape(gd, gd)

# Make plots.
fig, (ax1, ax2) = plt.subplots(1, 2)
# Gaussian filtered 2D histograms.
ax1.imshow(h_g.transpose(), origin='lower')
ax2.imshow(z.transpose(), origin='lower')

plt.show()