Почему цикл for с использованием double не завершается

Я просматриваю старые экзаменационные вопросы (в настоящее время первый год uni.) и мне интересно, может ли кто-нибудь объяснить немного более подробно, почему следующее for цикл не заканчивается, когда он должен. Почему это происходит? Я понимаю, что он пропускает 100.0 из-за ошибки округления или чего-то еще, но почему? 

for(double i = 0.0; i != 100; i = i +0.1){
    System.out.println(i);
}
27
floating-point-precision for-loop java

5 ответов

число 0.1 не может быть точно представлено в двоичном формате, так же как 1/3 не может быть точно представлено в десятичном формате, поэтому вы не можете гарантировать, что:

0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1==1

Это потому, что в бинарные:

0.1=(binary)0.00011001100110011001100110011001....... forever

однако двойник не может содержать бесконечную точность, и поэтому, как мы приближаемся 1/3 к 0.3333333, так и двоичное представление должно приближаться к 0.1.


Расширенная десятичная аналогия

In decimal вы можете найти, что

1/3+1/3+1/3
=0.333+0.333+0.333
=0.999

Это точно такая же проблема. Это не следует рассматривать как слабость чисел с плавающей запятой, поскольку наша собственная десятичная система имеет те же трудности (но для разных чисел кто-то с системой base-3 Нашел бы странным, что мы изо всех сил пытались представить 1/3). Однако этот вопрос необходимо учитывать.

демо

A live demo предусмотрено Андреа Ligios показывает эти ошибки построения.

42

компьютеры (по крайней мере нынешние) работает с двоичными данными. Кроме того, существует ограничение длины обработки компьютеров в их арифметических логических единицах (т. е. 32bits, 64bits и т. д.). Представление целых чисел в двоичной форме просто, наоборот, мы не можем сказать то же самое для плавающих точек. 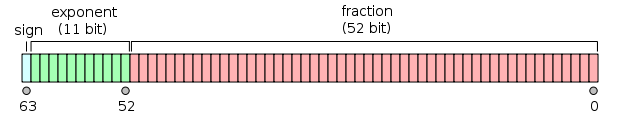64 bits floating point representation

Как показано выше, существует специальный способ представления плавающих точек в соответствии с IEEE-754, который также принимается в качестве defacto производителями процессоров и программными парнями вот почему важно, чтобы все об этом знали.

если мы посмотрим на максимальное значение double в java (Double.MAX_VALUE) равно 1.7976931348623157E308 (>10^307). только с 64 битами могут быть представлены огромные числа, однако проблема заключается в точности.

Как '==' и '!= 'операторы сравнивают числа побитово, в вашем случае 0.1+0.1+0.1 не равно 0,3 в терминах битов, которые они представлены.

В заключение, чтобы соответствовать огромным плавающим точечные числа в несколько бит умные инженеры решили пожертвовать точностью. Если вы работаете с плавающими точками, вы не должны использовать '= = 'или'!= 'если вы не уверены, что делаете.

11

как правило, никогда не используйте double для итерации из-за ошибок округления (0.1 может выглядеть хорошо, когда написано в базе 10, но попробуйте написать его в базе 2-что и есть double использует). Что вы должны сделать, это использовать простой int переменной для итерации и вычисления double от него.

for (int i = 0; i < 1000; i++)
  System.out.println(i/10.0);
10

прежде всего, я собираюсь объяснить некоторые вещи о двойниках. Это на самом деле будет происходить в базе 10 для удобства понимания.

возьмите значение одна треть и попробуйте выразить его в базе десять. Вы получаете 0.3333333333333.... Допустим, нам нужно обойти его на 4 места. Мы получаем 0.3333. Теперь добавим еще 1/3. Мы получаем 0.6666333333333.... какие раунды 0.6666. Добавим еще 1/3. Мы получаем 0.9999, не 1.

то же самое происходит с базой два и одна десятая. Так как вы идете на 0.110 и 0,110 является повторяющимся двоичным значением(например, 0.1666666... в базе десять), у вас будет достаточно ошибок, чтобы пропустить сто, когда вы туда доберетесь.

1/2 можно представить в основании 10 как раз отлично, и 1/5 может также. Это связано с тем, что простые факторы знаменателя являются подмножеством факторов базы. Это не относится к одной трети в базе десять или одной десятой в базе два.

8

Это должно быть для (double a = 0.0; a

попробуйте и посмотрите, работает ли это вместо

0