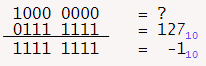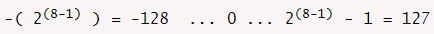Почему диапазон подписанного байта составляет от -128 до 127 (дополнение 2), а не от -127 до 127?

так это представление -128 10000000 или 110000000 ? Это representaion немного зависит ?

Да, представление дополнения 2 зависит от бит

почему бы просто не сделать нижний диапазон -127 fot 8 бит вместо написания -128 как 10000000

2^8 = 256. Поэтому, какую бы схему представления вы ни использовали, она должна представлять 256 различных значений.

а вы можете нарисовать круг, чтобы понять, как хорошая система дополнения 2.

сначала посмотрите на эту таблицу:

Bits    Unsigned 2's complement
00000000    0   0
00000001    1   1
00000010    2   2
01111110    126     126
01111111    127     127
10000000    128     −128
10000001    129     −127
10000010    130     −126
11111110    254     −2
11111111    255     −1

для системы дополнения 2 Вы можете нарисовать круг для понимания этой системы.

вот 4-битная версия. Вы можете легко разработать версию 8bit на себе. Этот круг представляет собой то, что на самом деле представляет собой система дополнения этого 2. Это круговая система. Это означает, что его представление зависит от "промежутка", который вы ему даете. вот почему 8-битная версия отрицательного числа будет отличаться от 16-разрядная версия того же отрицательного числа. вы можете сравнить то же отрицательное число в 4-битной версии, приведенной в круге, с 8-битной версией, приведенной в таблице.

                      0000  0
                 1111  -1     0001  1


        1110  -2                       0010  2




  1101  -3                                   0011  3



1100  -4                                       0100  4



  1011  -5                                   0101  5




        1010  -6                       0110  6


                 1001  -7     0111  7
                          1000  -8

на боковом примечании, арифметика дополнения 2 играет хорошо с" фиксированными " хранилищами вычислений ширины внутри компьютеров (регистры, память и т. д.).

в компьютерах первого поколения была тенденция предоставлять собственную десятичную арифметику. Но от этого быстро отказались в пользу "дополненного" или " циркулярного" схема потому, что десятичная арифметика причудлива с точки зрения компьютера. Мы находим это естественным, потому что"у нас 10 пальцев". Эти пальцы были самым ранним вычислительным инструментом нашего предка. вот почему мы считаем десятичную систему такой естественной. он встроен в наши гены.

альтернативой дополнению двух будет

• дополнения, который имеет проблемы из-за его "отрицательный нуль"
• знак/величина, который также имеет отрицательный ноль
• не присваивать значение 10000000, в этом случае многие функции, которые принимают подписанные 8-битные целые числа, должны будут проверить это недопустимое значение, теряя время. (Если ваш код не работает на гипотетическом оборудовании, которое обрабатывает этот битовый шаблон как целое число NaN.)

легче просто присвоить значение этому битовому шаблону, а естественным значением в представлении дополнения двух является -128.

например, в дополнение к двум, проверка отрицательных монтируется на проверку того, установлен ли его самый высокий бит. В варианте, где 10000000 недопустимо, это (псевдокод)

if (highest_bit_zero(x))
    return false;
else if (x == 0b10000000)
    ERROR
else
    return true;

вы решаете, как обрабатывать ошибку:)

так это представление -128 10000000 или 110000000 ? Это representaion немного зависит ?

в 9-битном мире это будет 110000000. В 16-битном мире это будет 1111111110000000. По крайней мере, пока мы говорим о дополнении двоих.

почему бы просто не сделать нижний диапазон -127 для 8 бит вместо записи -128 как 10000000 ?

Как larsmans указал, вы бы в конечном итоге с "недопустимое" значение, которое вы придется постоянно проверять. Дополнение два было выбрано, потому что это так легко для ALU обрабатывать. Точно так же, как ширина байтов была выбрана как сила двух (что также не всегда было так). На аппаратном уровне дополнение two идентично unsigned, поэтому никаких специальных инструкций или дополнительного оборудования не требуется (в отличие от дополнения one).

С вещами, как они есть, все значения с наибольшим набором битов отрицательны, все значения с самый высокий бит unset неотрицателен (положительный или нулевой). Легко, не так ли? Отрицательный диапазон на один больше положительного диапазона - это просто артефакт, пытающийся сохранить простое дополнение двух.

причина, почему вы не можете иметь диапазон от 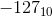до .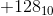

похоже 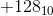и 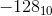представлены тем же шаблоном. Это нехорошо. Ненулевое целое число и его отрицательное не могут быть представлены одним и тем же шаблоном. Так что 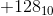не может быть представлен в восьми битах. Максимальное положительное целое число, которое может быть представлено в восьми битах .

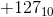какое число представлено 1000 0000? Добавьте представление 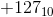для этого:

хороший выбор для ? is 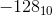. Поэтому 1000 0000 является 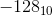. Восемь битов можно использовать для представления чисел 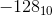... 0 ... .

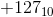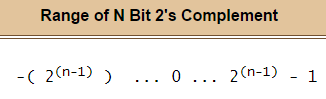
например, диапазон целых чисел, которые могут быть представлены в восьми битах с использованием дополнения two:

обратите внимание, что можно представить еще одно отрицательное целое число, чем положительные целые числа.

источник:http://programmedlessons.org/AssemblyTutorial/Chapter-08/ass08_20.html