почему градиентный спуск, когда мы можем решить линейную регрессию аналитически

в чем преимущество использования градиентного спуска в пространстве линейной регрессии? похоже, мы можем решить проблему (найти theta0-n, минимальную стоимость func) аналитическим методом, так почему мы все еще хотим использовать градиентный спуск, чтобы сделать то же самое? спасибо

63
gradient-descent linear-regression machine-learning

4 ответов

при использовании нормальных уравнений для решения функции затрат аналитически необходимо вычислить:

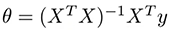
enter image description here

где X-матрица входных наблюдений и y-выходной вектор. Проблема с этой операцией заключается во временной сложности вычисления обратной матрицы nxn, которая равна O (n^3), и по мере увеличения n может занять очень много времени.

когда n низкое (n Градиентного Спуска намного быстрее, поэтому единственная причина-время:)

93

вы должны предоставить более подробную информацию о проблеме Youth-о чем именно вы спрашиваете - мы говорим о линейной регрессии в одном или многих измерениях? Простые или обобщенные?

В общем, почему люди используют GD?

  • это легко реализовать
  • это очень общий метод оптимизации-даже если вы измените свою модель на более общую, вы можете использовать ее

Так что насчет аналитических решений? Ну, мы!--11-->do используйте их, ваше утверждение здесь просто ложно (если мы говорим вообще), например OLS метод представляет собой замкнутую форму, аналитическое решение, которое широко используется. Если вы можете использовать аналитическое решение, оно доступно вычислительно (так как иногда GD просто дешевле или быстрее), то вы можете и даже должны использовать его.

Neverlethles это всегда вопрос некоторых плюсов и минусов-аналитические решения сильно связаны с модель, поэтому их реализация может быть неэффективной, если вы планируете обобщать / изменять свои модели в будущем. Иногда они менее эффективны, чем их численные аппроксимации, а иногда их просто сложнее реализовать. Если ни одно из вышеперечисленного не верно-вы должны использовать аналитическое решение, и люди делают это, действительно.

подводя итог, вы скорее используете GD над аналитическим решением, если:

  • вы рассматриваете изменения в модели, обобщения, добавление некоторых более сложных терминов / регуляризация / модификации
  • вам нужен общий метод, потому что вы мало знаете о будущем кода и модели (вы только один из разработчиков)
  • аналитическое решение дороже вычислительно, и вам нужна эффективность
  • аналитическое решение требует больше памяти, которой у вас нет
  • аналитическое решение трудно реализовать, и вам нужен простой, простой код
12

Я видел очень хороший ответ от https://stats.stackexchange.com/questions/23128/solving-for-regression-parameters-in-closed-form-vs-gradient-descent

в основном, причины:

1.Для большинства задач нелинейной регрессии решение замкнутой формы отсутствует.

2.Даже в линейной регрессии (одном из немногих случаев, когда доступно решение в замкнутой форме) может быть непрактично использовать формулу. В следующем примере показан один из способов в которой это может произойти.

7

другая причина заключается в том, что градиентный спуск сразу полезен при обобщении линейной регрессии, особенно если проблема не имеет решения в закрытой форме, например, в лассо (который добавляет термин регуляризации, состоящий из суммы абсолютных значений вектора веса).

0