ответ не содержит полного формального математического доказательства правильности. Я предположил, что здесь в этом нет необходимости. Кроме того, это было бы очень неразборчиво на SO (нет MathJax, например).
Я буду использовать (немного) specific премьер-факторизации. Это не лучший вариант, но достаточно.

tl; dr

мы хотим вычислить a^x mod m. Мы будем использовать функцию modpow(a,x,m). Описанный под.

1. если x достаточно мал (не экспоненциальная форма или существует p^x | m) просто вычислить его и вернуть
2. разделить на простые числа и вычислить p^x mod m отдельно для каждого штриха, используя Эйлера теорема. Цитата из Википедии:

   Эйлера теорема:
   Если n и a являются coprime положительные целые числа, тогда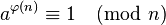 где φ (n) -Эйлера.

   предположение numbers are co-primeочень важно, как Nabb показывает в комментарий. Так, во-первых, мы должны убедиться, что эти числа взаимно простые. (Для большей ясности предположим x = b^(c^...).), Потому что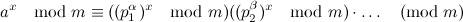 , где 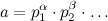мы можем разложить на множители a, и отдельно посчитать q1 = (p1^alpha)^x mod m,q2 = (p2^beta)^x mod m... и затем вычислить ответ в простой способ (q1 * q2 * q3 * ... mod m). Номер имеет самое большее o(log a) prime factors, поэтому мы будем вынуждены выполнять не более o(log a) расчетов.

   на самом деле нам не нужно разделяться на каждый простой фактор a (если не у всех случаются в m с другими экспонентами), и мы можем комбинировать с тем же показателем, но это не примечательно сейчас.

   теперь взгляните на на Θ(log c) времени. И после (используя тот же алгоритм) a^x' mod m, что равно решению.

   если x = b^(c^(d^...) мы решим его рекурсивно. Во-первых вычислить t1 = totient(m), после t2 = totient(t1) и так далее. Например,x=b^(c^d). Если t1=totient(m), a^x mod m = a^(b^(c^d) mod t1), и мы можем сказать b^(c^d) mod t1 = b^(c^d mod t2) mod t1, где t2 = totient(t1). все, что мы вычисляем, используя возведение в степень по квадрату алгоритма. Примечание: если некоторый тотиент не является со-простым к экспоненте, необходимо использовать тот же трюк, что и в основной задаче (на самом деле, мы должны забыть, что это экспонента и рекурсивно решить проблему, как в основной задаче). В приведенном выше примере, если t2 не является относительно простым с c, мы должны использовать этот трюк.

   вычислить φ(n)

   обратите внимание простой факты:

   1. если gcd(a,b)=1, потом φ(ab) = φ(a)*φ(b)
   2. если p это prime φ(p^k)=(p-1)*p^(k-1)

   поэтому мы можем факторизовать n (ak. n = p1^k1 * p2^k2 * ...) и отдельно посчитать φ(p1^k1),φ(p2^k2),..., используя факт 2. Затем объедините это, используя факт 1. φ(n)=φ(p1^k1)*φ(p2^k2)*...

   стоит помнить, что, если мы будем вычислять totient повторно, мы можем использовать сито Эратосфена и сохранить простые числа в таблице. Это позволит снизить постоянный.

   python пример: (это правильно, по той же причине, как этот алгоритм факторизации)

   def totient(n) :          # n - unsigned int
       result = 1
       p = 2                 #prime numbers - 'iterator'
       while p**2 <= n :
           if(n%p == 0) :    # * (p-1)
               result *= (p-1)
               n /= p
           while(n%p == 0) : # * p^(k-1)
               result *=  p
               n /= p
           p += 1
       if n != 1 :
           result *= (n-1)
       return result         # in O(sqrt(n))
   

   корпус: abc mod m

   потому что на самом деле он делает то же самое много раз, я считаю, что этот случай покажет вам, как решить это в целом.
   Во-первых, мы должны разделить a в расцвете сил. Лучший представление будет pair <number, exponent>.
   c++11 пример:

   std::vector<std::tuple<unsigned, unsigned>> split(unsigned n) {
     std::vector<std::tuple<unsigned, unsigned>> result;
     for(unsigned p = 2; p*p <= n; ++p) {
       unsigned current = 0;
       while(n % p == 0) {
         current += 1;
         n /= p;
        }
       if(current != 0)
        result.emplace_back(p, current);
      }
     if(n != 1)
      result.emplace_back(n, 1);
     return result;
    }
   

   после разделения, мы должны рассчитать (p^z)^(b^c) mod m=p^(z*(b^c)) mod m для каждой пары. Во-первых, мы должны проверить, если p^(z*(b^c)) | m. Если да, то ответ справедлив (p^z)^(b^c), но это возможно только в том случае, если z,b,c очень маленькие. Я считаю, что мне не нужно показывать ему пример кода.
   И, наконец, если p^(z*b^c) > m мы должны вычислить ответ. Во-первых, мы должны вычислить c' = gcd(m, p^(z*b^c)). После того, как мы сможем вычислить t = totient(m'). и (z*b^c - c' mod t). Это простой способ получить ответ.

   function modpow(p, z, b, c, m : integers) # (p^z)^(b^c) mod m
       c' = 0
       m' = m
       while m' % p == 0 :
           c' += 1
           m' /= p
       # now m' = m / gcd((p^z)^(b^c), m)
       t = totient(m')
       exponent = z*(b^c)-c' mod t
       return p^c' * (p^exponent mod m')
   

   и ниже Python работающего пример:

   def modpow(p, z, b, c, m) : # (p^z)^(b^c) mod m
       cp = 0
       while m % p == 0 :
           cp += 1
           m /= p              # m = m' now
       t = totient(m)
       exponent = ((pow(b,c,t)*z)%t + t - (cp%t))%t
                               # exponent = z*(b^c)-cp mod t
       return pow(p, cp)*pow(p, exponent, m)
   

   используя эту функцию, мы можем легко вычислить (p^z)^(b^c) mod m, после того, как мы просто несколько все результаты (mod m), мы также можем рассчитать все на постоянной основе. Пример ниже. (Надеюсь, я не ошибся, когда писал.) Достаточно велики только предположения, b, c (b^c > log(m) Ак. каждый p^(z*b^k) не делит m), это простая проверка, и я не вижу смысла делать беспорядок ею.

   def solve(a,b,c,m) : # split and solve
       result = 1
       p = 2            # primes
       while p**2 <= a :
           z = 0
           while a % p == 0 :
                        # calculate z
               a /= p
               z += 1
           if z != 0 :
               result *=  modpow(p,z,b,c,m)
               result %= m
           p += 1
       if a != 1 :      # Possible last prime
           result *= modpow(a, 1, b, c, m)
       return result % m
   

   похоже, это работает.
   демо и это правильно!