Поиск дерева Монте-Карло: реализация для крестики-нолики

Edit: Uploded полный исходный код, если вы хотите увидеть, можете ли вы заставить AI работать лучше:https://www.dropbox.com/s/ous72hidygbnqv6/MCTS_TTT.rar

Edit: пространство поиска ищется и перемещается, что приводит к потерям. Но ходы, приводящие к потерям, посещаются не очень часто из-за алгоритма UCT.

чтобы узнать о MCTS (Monte Carlo Tree Search), я использовал алгоритм для создания ИИ для классической игры в крестики-нолики. У меня есть реализован алгоритм с использованием следующей конструкции:

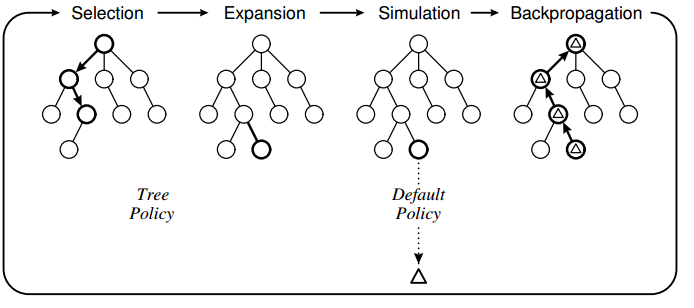Политика дерева основана на UCT, и политика по умолчанию должна выполнять случайные ходы до конца игры. Что я заметил с моей реализацией, так это то, что компьютер иногда делает ошибочные шаги, потому что он не "видит", что конкретный шаг приведет к потере напрямую.

например: 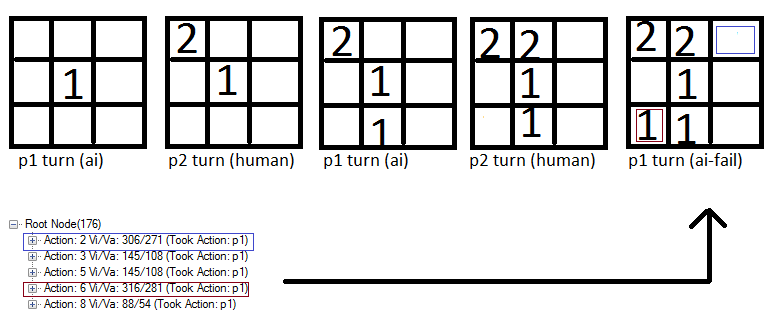Обратите внимание, что действие 6 (Красный квадрат) оценивается немного выше, чем синий квадрат и поэтому компьютер отмечает это место. Я думаю, это потому, что игровая политика основана на случайных ходах и поэтому существует хороший шанс, что человек не поставит "2" в синем поле. И если игрок не ставит 2 в синем поле, компьютер получает выигрыш.

Мои Вопросы

1) это известная проблема с MCTS или это результат неудачной реализации?

2) Какие могут быть возможные решения? Я думаю о ограничение движения на этапе выбора, но я не уверен :-)

код для основных MCTS:

    //THE EXECUTING FUNCTION
    public unsafe byte GetBestMove(Game game, int player, TreeView tv)
    {

        //Setup root and initial variables
        Node root = new Node(null, 0, Opponent(player));
        int startPlayer = player;

        helper.CopyBytes(root.state, game.board);

        //four phases: descent, roll-out, update and growth done iteratively X times
        //-----------------------------------------------------------------------------------------------------
        for (int iteration = 0; iteration < 1000; iteration++)
        {
            Node current = Selection(root, game);
            int value = Rollout(current, game, startPlayer);
            Update(current, value);
        }

        //Restore game state and return move with highest value
        helper.CopyBytes(game.board, root.state);

        //Draw tree
        DrawTree(tv, root);

        //return root.children.Aggregate((i1, i2) => i1.visits > i2.visits ? i1 : i2).action;
        return BestChildUCB(root, 0).action;
    }

    //#1. Select a node if 1: we have more valid feasible moves or 2: it is terminal 
    public Node Selection(Node current, Game game)
    {
        while (!game.IsTerminal(current.state))
        {
            List<byte> validMoves = game.GetValidMoves(current.state);

            if (validMoves.Count > current.children.Count)
                return Expand(current, game);
            else
                current = BestChildUCB(current, 1.44);
        }

        return current;
    }

    //#1. Helper
    public Node BestChildUCB(Node current, double C)
    {
        Node bestChild = null;
        double best = double.NegativeInfinity;

        foreach (Node child in current.children)
        {
            double UCB1 = ((double)child.value / (double)child.visits) + C * Math.Sqrt((2.0 * Math.Log((double)current.visits)) / (double)child.visits);

            if (UCB1 > best)
            {
                bestChild = child;
                best = UCB1;
            }
        }

        return bestChild;
    }

    //#2. Expand a node by creating a new move and returning the node
    public Node Expand(Node current, Game game)
    {
        //Copy current state to the game
        helper.CopyBytes(game.board, current.state);

        List<byte> validMoves = game.GetValidMoves(current.state);

        for (int i = 0; i < validMoves.Count; i++)
        {
            //We already have evaluated this move
            if (current.children.Exists(a => a.action == validMoves[i]))
                continue;

            int playerActing = Opponent(current.PlayerTookAction);

            Node node = new Node(current, validMoves[i], playerActing);
            current.children.Add(node);

            //Do the move in the game and save it to the child node
            game.Mark(playerActing, validMoves[i]);
            helper.CopyBytes(node.state, game.board);

            //Return to the previous game state
            helper.CopyBytes(game.board, current.state);

            return node;
        }

        throw new Exception("Error");
    }

    //#3. Roll-out. Simulate a game with a given policy and return the value
    public int Rollout(Node current, Game game, int startPlayer)
    {
        Random r = new Random(1337);
        helper.CopyBytes(game.board, current.state);
        int player = Opponent(current.PlayerTookAction);

        //Do the policy until a winner is found for the first (change?) node added
        while (game.GetWinner() == 0)
        {
            //Random
            List<byte> moves = game.GetValidMoves();
            byte move = moves[r.Next(0, moves.Count)];
            game.Mark(player, move);
            player = Opponent(player);
        }

        if (game.GetWinner() == startPlayer)
            return 1;

        return 0;
    }

    //#4. Update
    public unsafe void Update(Node current, int value)
    {
        do
        {
            current.visits++;
            current.value += value;
            current = current.parent;
        }
        while (current != null);
    }