Поиск кратчайшего пути в графе без отрицательных префиксов

Питер де Риваз указал в комментарии, что эта проблема включает ГАМИЛЬТОНОВ ПУТЬ как частный случай. Его объяснение было немного кратким, и мне потребовалось некоторое время, чтобы понять детали, поэтому я нарисовал несколько диаграмм для других, которые могли бы бороться. Я сделал этот пост сообщества wiki.

Я буду использовать следующий граф с шестью вершинами в качестве примера. Один из его гамильтоновых путей показан в смелый.

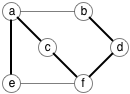
дан неориентированный граф с n вершины, для которых мы хотим найти Гамильтонов путь, мы строим новый взвешенный направленный граф с n² вершины, плюс начальные и конечные вершины. Обозначьте исходные вершины v_я и новые вершины w_ik для 0 ≤ я, k n. Если есть край между v_я и v_j в исходном графике, то для 0 ≤ k n-1 в новом графике есть ребра из w_ik to w_j(k+1) с весом -2^j и w_jk to w_я(k+1) с весом -2^я. Есть ребра от начала до w_{значения i0} с весом 2ⁿ - 2^я - 1 и от w_я(n-1) чтобы закончить с весом 0.

проще всего думать об этой конструкции как эквивалентной началу со счетом 2ⁿ - 1, а затем вычесть 2^я каждый раз, когда вы посещаете w_ij. (Вот как я нарисовал график ниже.)

каждый путь от начала до конца должен посетить точно n + 2 вершины (по одной из каждой строки, плюс начало и конец), поэтому единственный способ для суммы вдоль пути равняться нулю-это посетить каждый столбец ровно один раз.

Итак, вот исходный граф с шестью вершинами, преобразованными в новый граф с 38 вершинами. Исходный Гамильтонов путь соответствует пути, выделенному жирным шрифтом. Вы можете проверить, что сумма вдоль пути равна нулю.

обновление: у OP теперь было несколько раундов разъяснений, и теперь это другая проблема. Я оставлю это здесь для документирования моих идей для первой версии проблемы (или, скорее, моего понимания ее). Я попробую новый ответ для текущей версии проблемы. конец обновления

жаль, что ОП не прояснил некоторые из открытых вопросов. Я предполагаю следующее:

1. веса +/- 1.
2. N-количество вершин

первое предположение не является потерей общности, очевидно, но оно оказывает большое влияние на значение n (через второе предположение). Без первого предположения даже крошечный (фиксированный) граф может иметь произвольные длинные решения, изменяя веса без ограничений.

алгоритм, который я предлагаю, довольно прост и похож на известные алгоритмы графов. Я не эксперт по графикам, поэтому я могу использовать неправильные слова в несколько мест. Не стесняйтесь поправлять меня.

1. для исходной вершины, помните, стоимость 0. Добавить (source, 0) в список задач.
2. Pop элемент из списка задач. Следуйте всем исходящим ребрам вершины, вычисляя новую стоимость c, чтобы достичь новой вершины v. Если новая стоимость действительна (c >= 0 и c , см. ниже) и не запоминается для v,добавить он к запомненным значениям стоимости v и добавляет (v, c) к вашему todo список.
3. если список не пуст, перейдите к Шагу 2. (Или перерыв рано, если пункт назначения может быть достигнут со стоимостью 0).

ясно, что каждый "шаг", который не является непосредственным тупиком, создает новую комбинацию (вершина, стоимость). Из этих комбинаций будет сохранено не более n * n ^2 = n ^ 3, и, таким образом, в определенном смысле этот алгоритм равен O(n^3).

теперь, почему это находит оптимальный путь? у меня нет реальных доказательств, но я думаю, что следующие идеи оправдывают, почему я думаю, что этого достаточно, и возможно, что они могут быть превращены в реальное доказательство.

Я думаю, ясно, что единственное, что мы должны показать, это то, что условие c

во-первых, заметим, что любая (достижимая) вершина может быть достигнута стоимостью менее n.

пусть (v, c) является частью оптимального пути и c > n ^ 2. Как c > n, должен быть некоторый цикл на пути до достижения (v, c), где стоимость цикла равна 0 m2 > -n.

кроме того, пусть v будет достижим из источника со стоимостью 0

тогда мы можем построить пути от источника до v с затратами c1, С1 + М1, С1 + 2 * М1 ..., и пути от v до места назначения с затратами c2, c2 + m2, c2 + 2 * m2,... . Выберите 0

Если gcd m1 и m2 1, то цена будет 0. Если gcd > 1, то можно было бы выбрать другие циклы, чтобы gcd стал 1. Если это невозможно, то и нет. возможно оптимальное решение, и будет положительная стоимость для оптимального решения.

(Да, я вижу несколько проблем с этим попытка доказательства. Возможно, потребуется принять gcd нескольких положительных или отрицательных затрат цикла и т. д. Хотя меня бы очень заинтересовал контрпример.)

вот некоторые (Python) код:

def f(vertices, edges, source, dest):
    # vertices: unique hashable objects
    # edges: mapping (u, v) -> cost; u, v in vertices, cost in {-1, 1}

    #vertex_costs stores the possible costs for each vertex
    vertex_costs = dict((v, set()) for v in vertices)
    vertex_costs[source].add(0) # source can be reached with cost 0

    #vertex_costs_from stores for each the possible costs for each vertex the previous vertex
    vertex_costs_from = dict()

    # vertex_gotos is a convenience structure mapping a vertex to all ends of outgoing edges and their cost
    vertex_gotos = dict((v, []) for v in vertices)
    for (u, v), c in edges.items():
        vertex_gotos[u].append((v, c))

    max_c = len(vertices) ** 2 # the crucial number: maximal cost that's possible for an optimal path

    todo = [(source, 0)] # which vertices to look at

    while todo:
        u, c0 = todo.pop(0)
        for v, c1 in vertex_gotos[u]:
            c = c0 + c1
            if 0 <= c <= max_c and c not in vertex_costs[v]:
                vertex_costs[v].add(c)
                vertex_costs_from[v, c] = u
                todo.append((v, c))

    if not vertex_costs[dest]: # destination not reachable
        return None # or raise some Exception

    cost = min(vertex_costs[dest])

    path = [(dest, cost)] # build in reverse order
    v, c = dest, cost
    while (v, c) != (source, 0):
        u = vertex_costs_from[v, c]
        c -= edges[u, v]
        v = u
        path.append((v, c))

    return path[::-1] # return the reversed path

и вывод для некоторых графиков (ребра и их вес / путь / стоимость в каждой точке пути; извините, нет хорошие изображения):

AB+ BC+ CD+ DA+             AX+ XY+ YH+ HI- IJ- JK- KL- LM- MH-
 A  B  C  D  A  X  Y  H  I  J  K  L  M  H
 0  1  2  3  4  5  6  7  6  5  4  3  2  1
AB+ BC+ CD+ DE+ EF+ FG+ GA+ AX+ XY+ YH+ HI- IJ- JK- KL- LM- MH-
 A  B  C  D  E  F  G  A  B  C  D  E  F  G  A  B  C  D  E  F  G  A  X  Y  H  I  J  K  L  M  H  I  J  K  L  M  H  I  J  K  L  M  H  I  J  K  L  M  H
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1  0
AB+ BC+ CD+ DE+ EF+ FG+ GA+ AX+ XY+ YH+ HI- IJ- JK- KL- LM- MN- NH-
 A  X  Y  H
 0  1  2  3
AB+ BC+ CD+ DE+ EF+ FG+ GA+ AX+ XY+ YH+ HI- IJ- JK- KL- LM- MN- NO- OP- PH-
 A  B  C  D  E  F  G  A  B  C  D  E  F  G  A  B  C  D  E  F  G  A  B  C  D  E  F  G  A  B  C  D  E  F  G  A  B  C  D  E  F  G  A  X  Y  H  I  J  K  L  M  N  O  P  H  I  J  K  L  M  N  O  P  H  I  J  K  L  M  N  O  P  H  I  J  K  L  M  N  O  P  H  I  J  K  L  M  N  O  P  H
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1  0

вот код для получения этого вывода:

def find_path(edges, source, path):
    from itertools import chain

    print(edges)
    edges = dict(((u, v), 1 if c == "+" else -1) for u, v, c in edges.split())
    vertices = set(chain(*edges))

    path = f(vertices, edges, source, dest)
    path_v, path_c = zip(*path)
    print(" ".join("%2s" % v for v in path_v))
    print(" ".join("%2d" % c for c in path_c))

source, dest = "AH"

edges = "AB+ BC+ CD+ DA+             AX+ XY+ YH+ HI- IJ- JK- KL- LM- MH-"
# uv+ means edge from u to v exists and has cost 1, uv- = cost -1
find_path(edges, source, path)

edges = "AB+ BC+ CD+ DE+ EF+ FG+ GA+ AX+ XY+ YH+ HI- IJ- JK- KL- LM- MH-"
find_path(edges, source, path)

edges = "AB+ BC+ CD+ DE+ EF+ FG+ GA+ AX+ XY+ YH+ HI- IJ- JK- KL- LM- MN- NH-"
find_path(edges, source, path)

edges = "AB+ BC+ CD+ DE+ EF+ FG+ GA+ AX+ XY+ YH+ HI- IJ- JK- KL- LM- MN- NO- OP- PH-"
find_path(edges, source, path)

Как Kaganar ноты, мы должны сделать некоторые предположения для того, чтобы получить алгоритм polytime. Предположим, что длины ребер в {-1, 1}. Учитывая график, постройте взвешенную контекстно-свободную грамматику, которая распознает допустимые пути от источника к назначению с весом, равным числу избыточных 1 ребер (она обобщает грамматику для сбалансированных скобок). Вычислите для каждого нетерминала стоимость самого дешевого производства, инициализируя все до бесконечности или 1, в зависимости от того, есть ли производство, в котором RHS не имеет нетерминального, а затем расслабляющего n - 1 раз, где n-количество нетерминальных.

Я бы использовал рекурсию brute forcing здесь: что-то вроде (псевдо-код, чтобы убедиться, что это не языковые)

вам понадобится:

• 2D массив bools показывает, где вы можете и где вы не можете пойти, это не должно включать "Запрещенные значения", как и до отрицательного края, вы можете добавить вертикальный и горизонтальный "перевод", чтобы убедиться, что он начинается с [0][0]
• целое число (статическое), содержащее кратчайший путь
• 1Д массив из 2 слотов, показывающий цель. [0] = x, [1] = y

вы будете заниматься:

function(int xPosition, int yPosition, int steps)
{
if(You are at target AND steps < Shortest Path)
    Shortest Path = steps
if(This Position is NOT legal)
    /*exit function*/
else
    /*try to move in every legal DIRECTION, not caring whether the result is legal or not
    but always adding 1 to steps, like using:*/
    function(xPosition+1, yPosition, steps+1);
    function(xPosition-1, yPosition, steps+1);
    function(xPosition, yPosition+1, steps+1);
    function(xPosition, yPosition-1, steps+1);
}

тогда просто запустите его с функция (StartingX, StartingY, 0);

кратчайший путь будет содержаться в статическом внешнем int

Я хотел бы уточнить несколько моментов :

1. Да могут быть отрицательные циклы веса.
2. n-количество ребер.
3. веса произвольны не только +1 / -1.
4. предположим, что существует путь длины O(n), если проблема имеет решение. (N-количество ребер)

хотя люди показали, что быстрого решения не существует (если только P=NP)..

Я думаю, что для большинства графиков (95%+) вы должны быть в состоянии найти решение достаточно быстро.

Я использую тот факт, что если есть циклы, то обычно существует много решений, и нам нужно только найти один из них. Вероятно, в моих идеях есть некоторые вопиющие дыры, поэтому, пожалуйста, дайте мне знать.

Ideas:

1. найдите отрицательный цикл, который ближе всего к назначение. обозначим кратчайшее расстояние между циклом и назначения как D(конец,НАЭК)

2. найдите ближайший положительный цикл к стартовому узлу, обозначьте расстояние от старта как d (start,posC)

(Я рассуждаю в 95% графиков вы можете легко найти эти циклы)

    Now we have cases:
a) there is both the positive and negative cycles were found:
The answer is d(end,negC).

b) no cycles were found:
simply use shortest path algorithm?

c) Only one of the cycles was found. We note in both these cases the problem is the same due to symmetry (e.g. if we swap the weights and start/end we get the same problem). I'll just consider the case that there was a positive cycle found.

find the shortest path from start to end without going around the positive cycle. (perhaps using modified breadth first search or something). If no such path exists (without going positive).. then .. it gets a bit tricky.. we have to do laps of the positive cycle (and perhaps some percentage of a lap).
If you just want an approximate answer, work out shortest path from positive cycle to end node which should usually be some negative number. Calculate number of laps required to overcome this negative answer + the distance from the entry point to the cycle to the exit point of the cycle. Now to do better perhaps there was another node in the cycle you should have exited the cycle from... To do this you would need to calculate the smallest negative distance of every node in the cycle to the end node.. and then it sort of turns into a group theory/ random number generator type problem... do as many laps of the cycle as you want till you get just above one of these numbers.

удачи и, надеюсь, мои решения будут работать в большинстве случаев.

текущие допущения:

1. Да могут быть отрицательные циклы веса.
2. n-количество ребер.
3. предположим, что существует путь длины O(n), если проблема имеет решение.
4. +1/-1 края Весов.

мы можем без потери общности предположить, что число вершин не более n. Рекурсивно пройдите график и запомните значения затрат для каждой вершины. Остановитесь, если стоимость уже запомнилась вершины, или если стоимость будет отрицательной.

после шагов O(n) либо назначение не было достигнуто, и нет решения. В противном случае для каждой из o(n) вершин мы запомнили не более O(n) различных значений затрат, и для каждой из этих o (n ^ 2) комбинаций могло быть до n неудачных попыток перейти к другим вершинам. В общем, это O (n ^ 3). вопрос.е.д.

обновление: конечно, есть что-то подозрительное снова. Что? означает ли предположение 3: путь длины O(n) существует, если проблема имеет решение? Любое решение должно обнаружить это, потому что оно также должно сообщить, если нет решения. Но это невозможно обнаружить, потому что это не свойство отдельного графа, на котором работает алгоритм (это асимптотическое поведение).

(также ясно, что не все графики, для которых может быть достигнуто назначение, имеют путь решения длины O (n): возьмите цепочку из m ребер веса -1, а перед это простой цикл из M ребер и общего веса +1).

[теперь я понимаю, что большая часть кода-Python из моего другого ответа (попытка первая версия проблемы) могут быть использованы.]

Шаг 1: Обратите внимание, что ваш ответ будет не более 2*n (если оно существует).
Шаг 2: Создайте новый граф с вершинами, которые являются парами [vertex][cost]. (2 * n^2 вершины)
Шаг 3: Обратите внимание, что новый граф будет иметь все ребра, равные одному, и не более 2*n для каждой пары [вершина][стоимость].
Шаг 4: Сделайте dfs над этим графиком, начиная с [start][0]
Шаг 5: Найдите минимум k, такой, что [finish][k] доступен.

общая сложность не более O(n^2)*O (n) = O (n^3)

EDIT: уточнение на Шаге 1.
Если есть положительный цикл, доступный с самого начала, вы можете пройти весь путь до n. Теперь вы можете перейти к любой доступной вершине, не более чем по n ребрам, каждый из которых равен +1 или -1, оставляя вам диапазон [0;2n]. В противном случае вы пройдете либо через отрицательные циклы, либо не более n +1, которые не находятся в отрицательном цикле, оставляя вам диапазон [0;n].