Поиск min max фондового графика
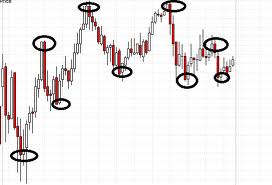
существуют ли какие-либо конкретные алгоритмы, которые позволят мне найти минимальные и максимальные точки На картинке выше?
У меня есть данные в текстовом формате, поэтому мне не нужно искать их на картинке. Проблема с акциями в том, что у них так много локальных минут, а простые производные не будут работать.
Я думаю использовать цифровые фильтры (домен z) и сглаживать график, но у меня все еще остается слишком много локализованных минимумов и максимумов.
Я также попытался использовать скользящую среднюю, чтобы сгладить график, но опять же у меня слишком много Максов и минут.
EDIT:
Я прочитал некоторые комментарии, и я просто не обводил некоторые минимумы и максимумы случайно.
Я думаю, что я придумал алгоритм, который может работать. Сначала найдите минимальные и максимальные точки (максимум дня и минимум дня). Затем нарисуйте три линии, одну от open до high или low, в зависимости от того, что наступит раньше затем линия от низкого к высокому или от высокого к низкому и, наконец, к закрытию. Затем в каждой из этих трех областей найдите точку, наиболее удаленную от линии, как мои максимум и минимум, а затем повторите цикл.
8 ответов
обычно я использую комбинацию скользящей средней и экспоненциальной скользящей средней. Он оказался (эмпирически) хорошо приспособленным для этой задачи (по крайней мере, для моих нужд). Результаты настраиваются только с двумя параметрами. Вот пример:
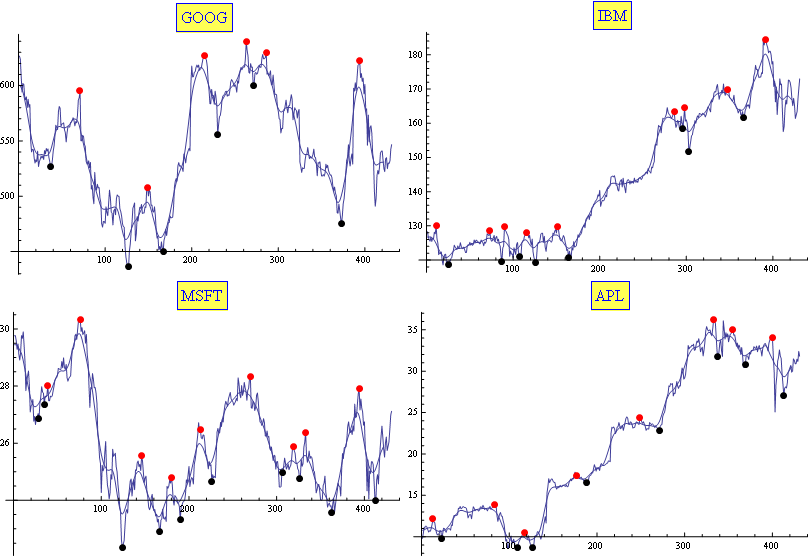
редактировать
в случае, если это полезно для кого-то, вот мой код в Mathematica:
f[sym_] := Module[{l},
(*get data*)
l = FinancialData[sym, "Jan. 1, 2010"][[All, 2]];
(*perform averages*)
l1 = ExponentialMovingAverage[MovingAverage[l, 10], .2];
(*calculate ma and min positions in the averaged list*)
l2 = {#[[1]], l1[[#[[1]]]]} & /@
MapIndexed[If[#1[[1]] < #1[[2]] > #1[[3]], #2, Sequence @@ {}] &,
Partition[l1, 3, 1]];
l3 = {#[[1]], l1[[#[[1]]]]} & /@
MapIndexed[If[#1[[1]] > #1[[2]] < #1[[3]], #2, Sequence @@ {}] &,
Partition[l1, 3, 1]];
(*correlate with max and mins positions in the original list*)
maxs = First /@ (Ordering[-l[[#[[1]] ;; #[[2]]]]] + #[[1]] -
1 & /@ ({4 + #[[1]] - 5, 4 + #[[1]] + 5} & /@ l2));
mins = Last /@ (Ordering[-l[[#[[1]] ;; #[[2]]]]] + #[[1]] -
1 & /@ ({4 + #[[1]] - 5, 4 + #[[1]] + 5} & /@ l3));
(*Show the plots*)
Show[{
ListPlot[l, Joined -> True, PlotRange -> All,
PlotLabel ->
Style[Framed[sym], 16, Blue, Background -> Lighter[Yellow]]],
ListLinePlot[ExponentialMovingAverage[MovingAverage[l, 10], .2]],
ListPlot[{#, l[[#]]} & /@ maxs,
PlotStyle -> Directive[PointSize[Large], Red]],
ListPlot[{#, l[[#]]} & /@ mins,
PlotStyle -> Directive[PointSize[Large], Black]]},
ImageSize -> 400]
]
Я не знаю, что вы подразумеваете под "простыми производными". Я понимаю, что это означает, что вы протестировали градиентного спуска и нашли его неудовлетворительным из-за обилия локальных экстремумов. Если да, то вы хотите посмотреть на имитация отжига:
отжиг металлургический процесс используемый для того чтобы закалить металлы через топление и охлаждая обработку. (...). Эти неровности обусловлены тем, что атомы застряли в неправильном месте структуры. В в процессе отжига металл нагревается и затем медленно остывает. Нагревание дает атомам энергию, необходимую им для расплавления, а медленный период охлаждения позволяет им перемещаться в правильное место в структуре.
(...) Однако, чтобы избежать локального Оптима,алгоритм будет иметь вероятность сделать шаг в плохом направлении: другими словами, сделать шаг, который увеличивает значение для задачи минимизации или это уменьшает значение задачи максимизации. Для моделирования процесса отжига эта вероятность будет частично зависеть от параметра" температура " в алгоритме, который инициализируется при высоком значении и уменьшается на каждой итерации. Следовательно,алгоритм изначально будет иметь высокую вероятность отхода от ближайшего (вероятного локального) оптимума. На итерациях эта вероятность будет уменьшаться, и алгоритм сойдется на (Надеюсь, глобальном) оптимуме у него не было шанса сбежать. (источник, cuts &, акцент мой)
Я знаю этот локальный Оптима-это именно то, что круги в вашем чертеже представляют, выше, и, следовательно, то, что вы хотите найти. Но, как я интерпретирую цитату "так много локальных мин и Максов простые производные не будут работать.", это тоже именно то, что вы находите слишком много. Я предполагаю, что у вас проблемы со всеми "зигзагами", которые вы делаете кривой между две обведенные точки.
все, что, похоже, отличает Оптиму, которую вы обводите от остальных точек кривой, - это их глобальность, а именно: найти нижнюю точку чем первая точка, которую вы обведете слева вам нужно дальше до в любом случае в координате x, чем вам нужно сделать то же самое для своих близких соседей. Вот что дает отжиг: в зависимости от параметр температуры, вы можете контролировать размер скачков, которые вы позволяете себе сделать. Там и быть значением, для которого вы ловите" большие " локальные Оптимы, и все же пропускаете "маленькие". То, что я предлагаю, не революционно: есть несколько примеров (например,1 2), где люди получали хорошие результаты от таких шумных данных.
вы заметите, что многие ответы идут на производные с какой-то фильтрацией низких частот. Какая-то скользящая средняя, если хотите. И БПФ, и скользящая средняя квадратного окна, и экспоненциальная скользящая средняя очень похожи на фундаментальном уровне. Однако, учитывая выбор по всем скользящим средним, какой из них лучший?
ответ: гауссова скользящая средняя; это нормальное распределение, о котором вы знаете.
в причина: гауссов фильтр-единственный фильтр, который никогда не будет производить "поддельный" максимум; максимум, которого не было с самого начала. Это было теоретически доказано как для непрерывных, так и для дискретных данных (убедитесь, что вы используете дискретный гауссовский для дискретных данных!). По мере увеличения гауссовой Сигмы локальные максимумы и минимумы будут сливаться самым интуитивным образом. Таким образом, если вы хотите, чтобы было не более одного локального максимума в день, вы устанавливаете Сигму в один и т. д.
просто определите, что вы подразумеваете под минимумом и максимумом точным, но настраиваемым способом, а затем настройте его, пока он не найдет нужное количество минимумов и максимумов. Например, сначала можно сгладить график, заменив каждое значение средним этого значения и N значений слева и справа от него. Увеличивая N, вы можете уменьшить количество найденных минимумов и максимумов.
затем вы можете определить минимум как точку, где, если вы пропустите значения a влево и вправо, следующие значения B все показать устойчивую тенденцию к росту. Увеличивая B, вы можете найти меньше минимумов и максимумов. Регулируя A, вы можете настроить, как "плоский" минимум или максимум разрешено быть.
Как только вы используете настраиваемый алгоритм, вы можете просто настроить его, пока он не выглядит правильно.
можно использовать метод сплайн создать contenous аппроксимации полинома к вашей первоначальной функции [с пожеланной степенью]. После того, как у вас есть этот полином, найдите локальный минимум/максимум [используя базовое исчисление] на нем [сгенерированный полином].
обратите внимание, что метод сплайна дает вам полином аппроксимации, который является "гладким", поэтому легко найти локальные min / maxs и оба как можно ближе к исходной функции, и, следовательно, локальный min / max должен быть очень близок к истинному значению в исходной функции.
для повышения точности, после нахождения локальных минут / Макс в сгенерированном полиноме, для каждого x0 которые представляют собой локальный min / max, вы должны смотреть во всех x так, что x0-delta < x < x0 + delta, чтобы найти реальный min / max, который представляет эта точка.
Я часто обнаруживал, что экстремумы, субъективно воспринимаемые людьми (читай: единственные экстремумы на фондовых графиках, которые в основном представляют собой случайный шум), часто можно найти после фильтрации Фурье-диапазона. Вы можете попробовать этот алгоритм:
- выполните FFT
- сделайте полосу пропускания в частотном пространстве. Выберите Параметры bandpass на основе диапазона данных, которые вы хотите, чтобы ваши экстремумы выглядели хорошо, то есть временной шкалы интереса.
- выполнить обратное быстрое преобразование Фурье.
- выберите локальные максимумы результирующей кривой.
параметры второго шага кажутся довольно субъективными, но опять же, субъективность-это сама природа анализа фондовых диаграмм.
Как упоминалось велисарием, лучший метод, по-видимому, включает фильтрацию данных гладко. При достаточном сглаживании поиск изменений в склоне должен указывать на локальные мины и максы (здесь поможет производная). Я бы использовал центрированное скользящее окно для текущей медианы / среднего или текущего EMA (или аналогичного фильтра IIR).
