Поиск точек пересечения двух эллипсов (Python)
Я пишу базовую библиотеку 2D-форм в Python (в первую очередь для манипулирования чертежами SVG), и я в недоумении, как эффективно вычислить точки пересечения двух эллипсов.
каждый эллипс определяется следующими переменными (все поплавки):
c: center point (x, y)
hradius: "horizontal" radius
vradius: "vertical" radius
phi: rotation from coordinate system's x-axis to ellipse's horizontal axis
игнорирование, когда эллипсы идентичны, может быть от 0 до 4 точек пересечения (без пересечения, касательной, частично перекрывающейся, частично перекрывающейся и внутренне касательной и полностью перекрытие.)
Я нашел несколько возможных решений:
- модуль геометрии SymPy - это в основном просто подключает уравнения эллипса к решателю Симпи. Я не уверен, что это имеет смысл, не имея уже решателя. (Кстати, я бы использовал SymPy вместо того, чтобы катить свой собственный, но он ужасно работает, когда имеет дело с сумасшедшими поплавками)
- как определить, пересекается ли эллипс (сталкивается с) a круг - это, вероятно, может быть адаптировано для двух эллипсов, но я немного нечетко понимаю, как превратить его в разумный код.
- как эллипс к пересечению эллипса? - библиотека ссылок на ответы (CADEMIA) может иметь хороший алгоритм, но я даже не могу понять, является ли он открытым исходным кодом.
- Википедия: Пересечение Двух Коник - у меня недостаточно понимания линейной алгебры, чтобы понять это решение.
любые предложения о том, как я должен идти о расчете пересечений? Скорость (возможно, придется рассчитать много пересечений) и элегантность являются основными критериями. Код был бы фантастическим,но даже хорошее направление было бы полезно.
3 ответов
в математике вам нужно выразить эллипсы как двумерные квадратичные уравнения и решить их. Я нашел doucument. Все вычисления находятся в документе, но для его реализации в Python может потребоваться некоторое время.
таким образом, другой метод-аппроксимировать эллипсы как полилинии и использовать shapely для поиска пересечений, вот код:
import numpy as np
from shapely.geometry.polygon import LinearRing
def ellipse_polyline(ellipses, n=100):
t = linspace(0, 2*np.pi, n, endpoint=False)
st = np.sin(t)
ct = np.cos(t)
result = []
for x0, y0, a, b, angle in ellipses:
angle = np.deg2rad(angle)
sa = np.sin(angle)
ca = np.cos(angle)
p = np.empty((n, 2))
p[:, 0] = x0 + a * ca * ct - b * sa * st
p[:, 1] = y0 + a * sa * ct + b * ca * st
result.append(p)
return result
def intersections(a, b):
ea = LinearRing(a)
eb = LinearRing(b)
mp = ea.intersection(eb)
x = [p.x for p in mp]
y = [p.y for p in mp]
return x, y
ellipses = [(1, 1, 2, 1, 45), (2, 0.5, 5, 1.5, -30)]
a, b = ellipse_polyline(ellipses)
x, y = intersections(a, b)
plot(x, y, "o")
plot(a[:,0], a[:,1])
plot(b[:,0], b[:,1])
и выход:
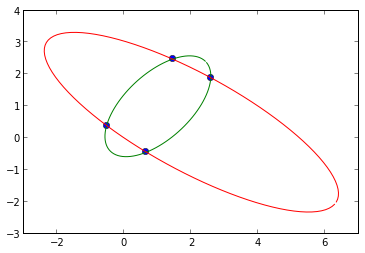
на моем ПК требуется около 1,5 МС.
смотрим sympy Я думаю, что в нем есть все, что вам нужно. (Я попытался предоставить вам примеры кодов; к сожалению, мне не удалось установить sympy с gmpy2 вместо бесполезной встроенной математики python)
у вас есть :
- an эллипс С поворот метод, который может быть пересекает С другими эллипсы
- или произвольные пересечения функция, которая принимает variadic количество.. то, что они называют "геометрическими сущностями".
из их примеров я думаю, что определенно можно пересечь два эллипса:
>>> from sympy import Ellipse, Point, Line, sqrt
>>> e = Ellipse(Point(0, 0), 5, 7)
...
>>> e.intersection(Ellipse(Point(1, 0), 4, 3))
[Point(0, -3*sqrt(15)/4), Point(0, 3*sqrt(15)/4)]
>>> e.intersection(Ellipse(Point(5, 0), 4, 3))
[Point(2, -3*sqrt(7)/4), Point(2, 3*sqrt(7)/4)]
>>> e.intersection(Ellipse(Point(100500, 0), 4, 3))
[]
>>> e.intersection(Ellipse(Point(0, 0), 3, 4))
[Point(-363/175, -48*sqrt(111)/175), Point(-363/175, 48*sqrt(111)/175),
Point(3, 0)]
>>> e.intersection(Ellipse(Point(-1, 0), 3, 4))
[Point(-17/5, -12/5), Point(-17/5, 12/5), Point(7/5, -12/5),
Point(7/5, 12/5)]
edit: поскольку общий эллипс (ax^2 + bx + cy^2 + dy + exy + f) не поддерживается в sympy,
вы должны построить уравнения и преобразовать их самостоятельно и использовать их решатель для поиска точек пересечения.
вы можете использовать метод, показанный здесь: https://math.stackexchange.com/questions/864070/how-to-determine-if-two-ellipse-have-at-least-one-intersection-point/864186#864186
сначала вы должны иметь возможность масштабировать эллипс в одном направлении. Для этого необходимо вычислить коэффициенты эллипса в виде конического сечения, масштабировать, а затем восстановить новые геометрические параметры эллипса: центр, оси, угол.
тогда ваша задача сводится к найти расстояние от эллипса до начала координат. Чтобы решить эту последнюю проблему, вам нужна некоторая итерация. Вот возможная самостоятельная реализация...
from math import *
def bisect(f,t_0,t_1,err=0.0001,max_iter=100):
iter = 0
ft_0 = f(t_0)
ft_1 = f(t_1)
assert ft_0*ft_1 <= 0.0
while True:
t = 0.5*(t_0+t_1)
ft = f(t)
if iter>=max_iter or ft<err:
return t
if ft * ft_0 <= 0.0:
t_1 = t
ft_1 = ft
else:
t_0 = t
ft_0 = ft
iter += 1
class Ellipse(object):
def __init__(self,center,radius,angle=0.0):
assert len(center) == 2
assert len(radius) == 2
self.center = center
self.radius = radius
self.angle = angle
def distance_from_origin(self):
"""
Ellipse equation:
(x-center_x)^2/radius_x^2 + (y-center_y)^2/radius_y^2 = 1
x = center_x + radius_x * cos(t)
y = center_y + radius_y * sin(t)
"""
center = self.center
radius = self.radius
# rotate ellipse of -angle to become axis aligned
c,s = cos(self.angle),sin(self.angle)
center = (c * center[0] + s * center[1],
-s* center[0] + c * center[1])
f = lambda t: (radius[1]*(center[1] + radius[1]*sin(t))*cos(t) -
radius[0]*(center[0] + radius[0]*cos(t))*sin(t))
if center[0] > 0.0:
if center[1] > 0.0:
t_0, t_1 = -pi, -pi/2
else:
t_0, t_1 = pi/2, pi
else:
if center[1] > 0.0:
t_0, t_1 = -pi/2, 0
else:
t_0, t_1 = 0, pi/2
t = bisect(f,t_0,t_1)
x = center[0] + radius[0]*cos(t)
y = center[1] + radius[1]*sin(t)
return sqrt(x**2 + y**2)
print Ellipse((1.0,-1.0),(2.0,0.5)).distance_from_origin()
