Показать пересечение двух кривых

Если у меня есть два графика, определенные двумя разными уравнениями:

x = 0:0.01:30;
y1 = x .^2 + 2;
y2 = x .^3 ;

и я строю их как 

plot(x, y1, x, y2);

Как получить небольшое кольцо вокруг точки пересечения программно (как на следующем графике)?

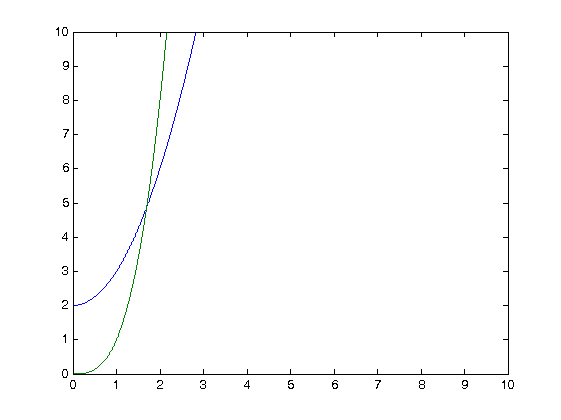
enter image description here

7
graph intersection matlab plot

5 ответов

вам нужно будет найти точку пересечения (px, py) вручную:

idx = find(y1 - y2 < eps, 1); %// Index of coordinate in array
px = x(idx);
py = y1(idx);

помните, что мы сравниваем два числа в представлении с плавающей запятой, поэтому вместо y1 == y2 мы должны установить допуск. Я выбрал его как eps, но это зависит от вас, чтобы решить.

чтобы нарисовать круг вокруг этой точки, вы можете вычислить ее точки, а затем построить их, но лучшим подходом было бы построить одну точку с маркером взорванного круга (кредит Джонас это предложение):

plot(px, py, 'ro', 'MarkerSize', 18)

таким образом, размеры круга не зависят от осей и соотношения сторон графика.

пример

x = 0:0.01:30;
y1 = x .^ 2 + 2;
y2 = x .^ 3;

%// Find point of intersection
idx = find(y1 - y2 < eps, 1);
px = x(idx);
py = y1(idx);

figure
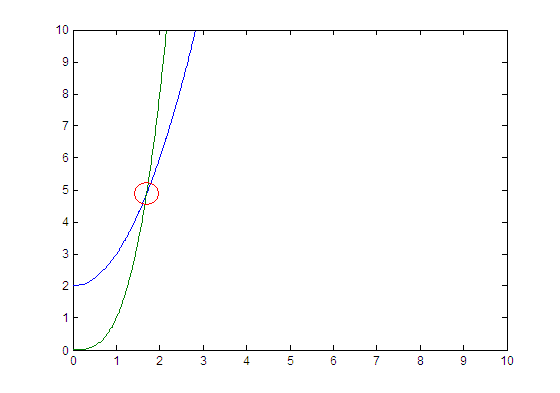
plot(x, y1, x, y2, px, py, 'ro', 'MarkerSize', 18)
axis([0 10 0 10])

Это должно привести к следующему сюжету: result

11

в вашем примере, когда у вас есть x, y1 и y2 Что вы можете сделать, это

idx = find(abs(y1 - y2) == min(abs(y1 - y2)));
xInter = x(idx)
yInter = y1(idx) % or y2(idx)

Если у вас есть x1, y1 и x2, y2, где x1 ~= x2 вы можете сначала сделать 1D интерполяцию, используя

yy2 = interp1(x2, y2, x1);

затем применить

idx = find(abs(y1 - yy2) == min(abs(y1 - yy2)));
xInter = x1(idx)
yInter = y1(idx) % or yy2(idx)
2

отличный пост @EitanT, однако я хотел бы дополнить это другим (автоматизированным) способом поиска пересечения (при условии, что он есть, и графики ведут себя хорошо).

вот наша отправная точка:

x = 0:0.01:30;
y1 = x .^2 + 2;
y2 = x .^3 ;

прежде всего, мы проверяем, точно ли эти значения равны, для недискретных ситуаций с неплавающей точкой этого должно быть достаточно:

idx = find(y1==y2)

если они никогда не записываются, чтобы быть точно равными, пересечение происходит, если одно превосходит другое, поэтому мы смотрим на разницу:

if isempty(idx)
  d = y1-y2;
  % At the moment of crossing, the sign will change:
  s = diff(sign(d));
  % Now just find the point where it changes
  f = find(s,1);
end

чтобы суммировать это в компактной форме без дополнительных переменных, я бы рекомендовал использовать:

idx = find(y1==y2)
if isempty(idx)
idx = find(diff(sign(y1-y2)),1)
end
1

особенно при знании функций можно использовать символический математический набор инструментов.

y1 = x .^2 + 2;
y2 = x .^3 ;
syms x real
intersection=simplify(solve(y1==y2))

использовать vpa(intersection) преобразовать в число или double(intersection) чтобы преобразовать его в значение с плавающей запятой.

1

последнее, но не менее, пожалуй, самый чистый способ сделать это-команда polyxpoly:

[xi,yi] = polyxpoly(x,y1,x,y2)

xi = 1.69560153754948
yi = 4.87508921229275

удачи!

0