Полиномиальная регрессия в R - с дополнительными ограничениями на кривой
Я знаю, как сделать базовую полиномиальную регрессию в R. Однако я могу использовать только nls или lm чтобы соответствовать линии, которая минимизирует ошибку с точками.
это работает большую часть времени, но иногда, когда в данных есть пробелы в измерениях, модель становится очень интуитивной. Есть ли способ добавить дополнительные ограничения?
Воспроизводимый Пример:
Я хочу подогнать модель к следующим составленным данным (подобным моему реальному data):
x <- c(0, 6, 21, 41, 49, 63, 166)
y <- c(3.3, 4.2, 4.4, 3.6, 4.1, 6.7, 9.8)
df <- data.frame(x, y)
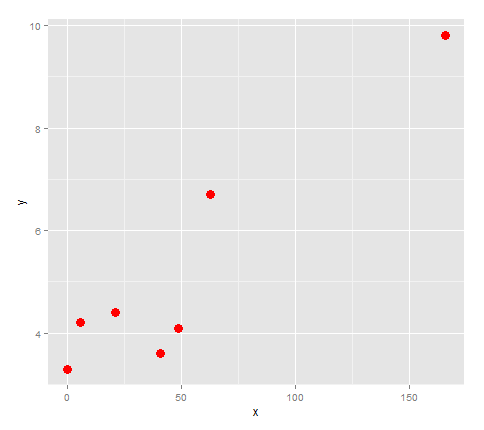
во-первых, давайте проложим его.
library(ggplot2)
points <- ggplot(df, aes(x,y)) + geom_point(size=4, col='red')
points
похоже, что если бы мы связали эти точки с линией, она бы изменила направление 3 раза, поэтому давайте попробуем подогнать к ней квартику.
lm <- lm(formula = y ~ x + I(x^2) + I(x^3) + I(x^4))
quartic <- function(x) lm$coefficients[5]*x^4 + lm$coefficients[4]*x^3 + lm$coefficients[3]*x^2 + lm$coefficients[2]*x + lm$coefficients[1]
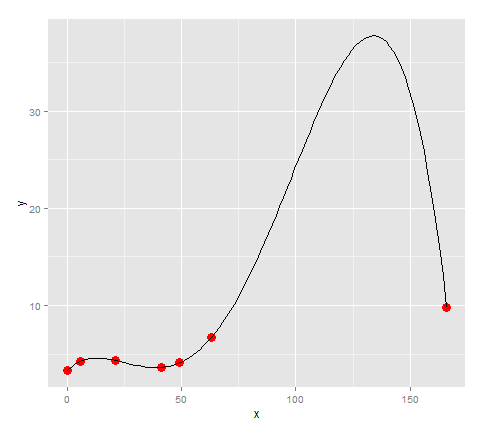
points + stat_function(fun=quartic)
похоже, что модель подходит для точек довольно хорошо... за исключением того, что наши данные имели большой разрыв между 63 и 166, есть огромный всплеск, который не имеет причин быть в модель. (Для моих фактических данных я знаю, что там нет огромного пика)
Итак, вопрос в этом случае:
- как я могу установить этот локальный максимум (166, 9.8)?
если это невозможно, то другой способ сделать это было бы:
- как я могу ограничить значения y, предсказанные линией, от того, чтобы стать больше, чем y=9.8.
или, возможно, есть лучше модель, котор нужно использовать? (Кроме как делать это по кусочкам). Моя цель-сравнить особенности моделей между графами.
3 ответов
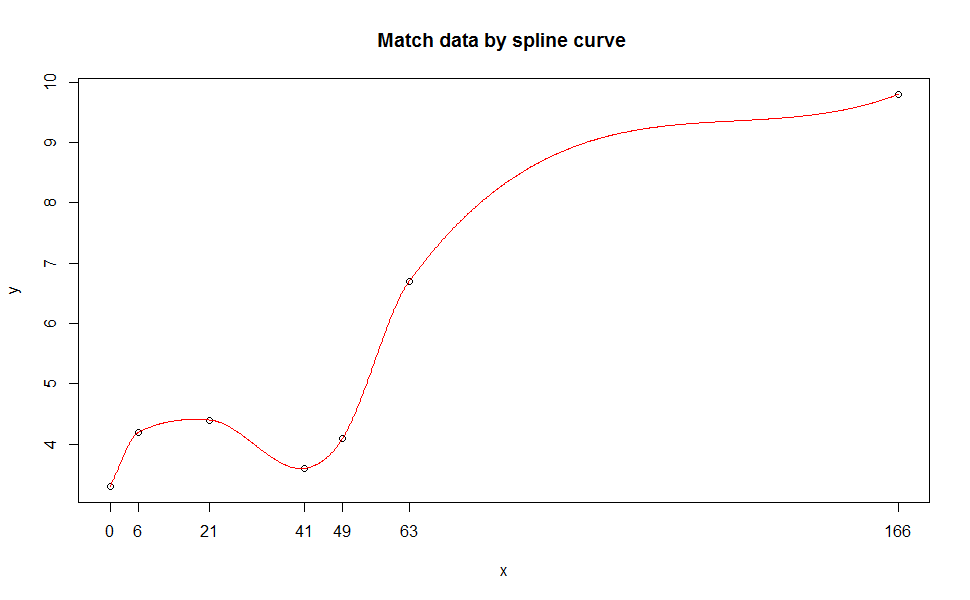
на spline тип функции будет идеально соответствовать вашим данным (но не для целей прогнозирования). Сплайн-кривые широко используются в областях САПР, и иногда это просто соответствует точке данных в математике и может быть отсутствием физического смысла по сравнению с регрессией. Дополнительная информация в здесь и большой фон введение в здесь.
на example(spline) покажет вам много причудливых примеров, и на самом деле я использую один из их.
далее, будет более разумно попробовать больше точек данных, а затем соответствовать lm или nls регрессия для прогнозирования.
пример кода:
library(splines)
x <- c(0, 6, 21, 41, 49, 63, 166)
y <- c(3.3, 4.2, 4.4, 3.6, 4.1, 6.7, 9.8)
s1 <- splinefun(x, y, method = "monoH.FC")
plot(x, y)
curve(s1(x), add = TRUE, col = "red", n = 1001)
другой подход, который я могу подумать, - это ограничение диапазона параметров в регрессии, чтобы вы могли получить прогнозируемые данные в ожидаемом диапазоне.
очень простой код optim внизу, но только выбор.
dat <- as.data.frame(cbind(x,y))
names(dat) <- c("x", "y")
# your lm
# lm<-lm(formula = y ~ x + I(x^2) + I(x^3) + I(x^4))
# define loss function, you can change to others
min.OLS <- function(data, par) {
with(data, sum(( par[1] +
par[2] * x +
par[3] * (x^2) +
par[4] * (x^3) +
par[5] * (x^4) +
- y )^2)
)
}
# set upper & lower bound for your regression
result.opt <- optim(par = c(0,0,0,0,0),
min.OLS,
data = dat,
lower=c(3.6,-2,-2,-2,-2),
upper=c(6,1,1,1,1),
method="L-BFGS-B"
)
predict.yy <- function(data, par) {
print(with(data, ((
par[1] +
par[2] * x +
par[3] * (x^2) +
par[4] * (x^3) +
par[5] * (x^4))))
)
}
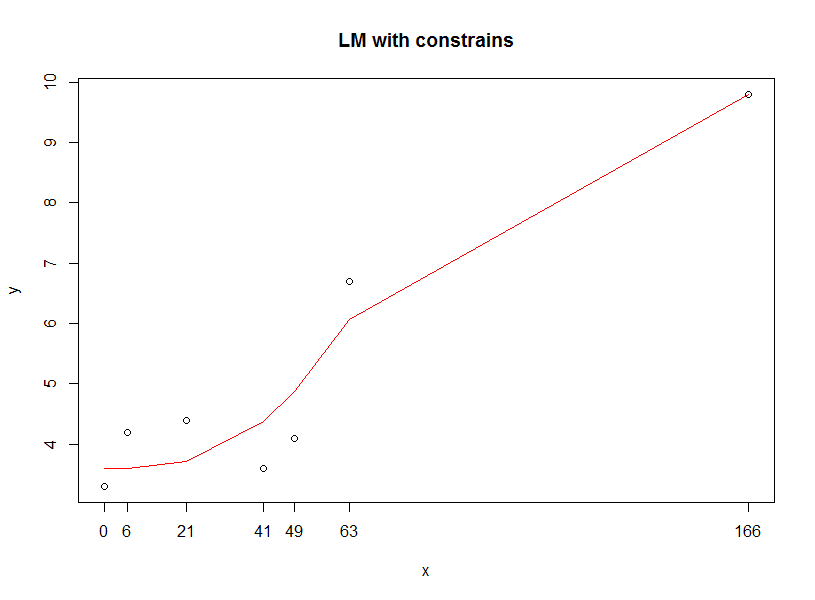
plot(x, y, main="LM with constrains")
lines(x, predict.yy(dat, result.opt$par), col="red" )
Я бы пошел на локальную регрессию, как предложил eipi10. Однако, если вы хочу чтобы иметь полиномиальную регрессию, вы можете попытаться минимизировать штрафную сумму квадратов.
вот пример, когда функция наказывается за отклонение "слишком много" от прямой линии:
library(ggplot2)
library(maxLik)
x <- c(0, 6, 21, 41, 49, 63, 166)/100
y <- c(3.3, 4.2, 4.4, 3.6, 4.1, 6.7, 9.8)
df <- data.frame(x, y)
points <- ggplot(df, aes(x,y)) + geom_point(size=4, col='red')
polyf <- function(par, x=df$x) {
## the polynomial function
par[1]*x + par[2]*x^2 + par[3]*x^3 + par[4]*x^4 + par[5]
}
quarticP <- function(x) {
polyf(par, x)
}
## a evenly distributed set of points, penalize deviations on these
grid <- seq(range(df$x)[1], range(df$x)[2], length=10)
objectiveF <- function(par, kappa=0) {
## Calculate penalized sum of squares: penalty for deviating from linear
## prediction
PSS <- sum((df$y - polyf(par))^2) + kappa*(pred1 - polyf(par))^2
-PSS
}
## first compute linear model prediction
res1 <- lm(y~x, data=df)
pred1 <- predict(res1, newdata=data.frame(x=grid))
points <- points + geom_smooth(method='lm',formula=y~x)
print(points)
## non-penalized function
res <- maxBFGS(objectiveF, start=c(0,0,0,0,0))
par <- coef(res)
points <- points + stat_function(fun=quarticP, col="green")
print(points)
## penalty
res <- maxBFGS(objectiveF, start=c(0,0,0,0,0), kappa=0.5)
par <- coef(res)
points <- points + stat_function(fun=quarticP, col="yellow")
print(points)
результат с пенальти 0.5 выглядит так:
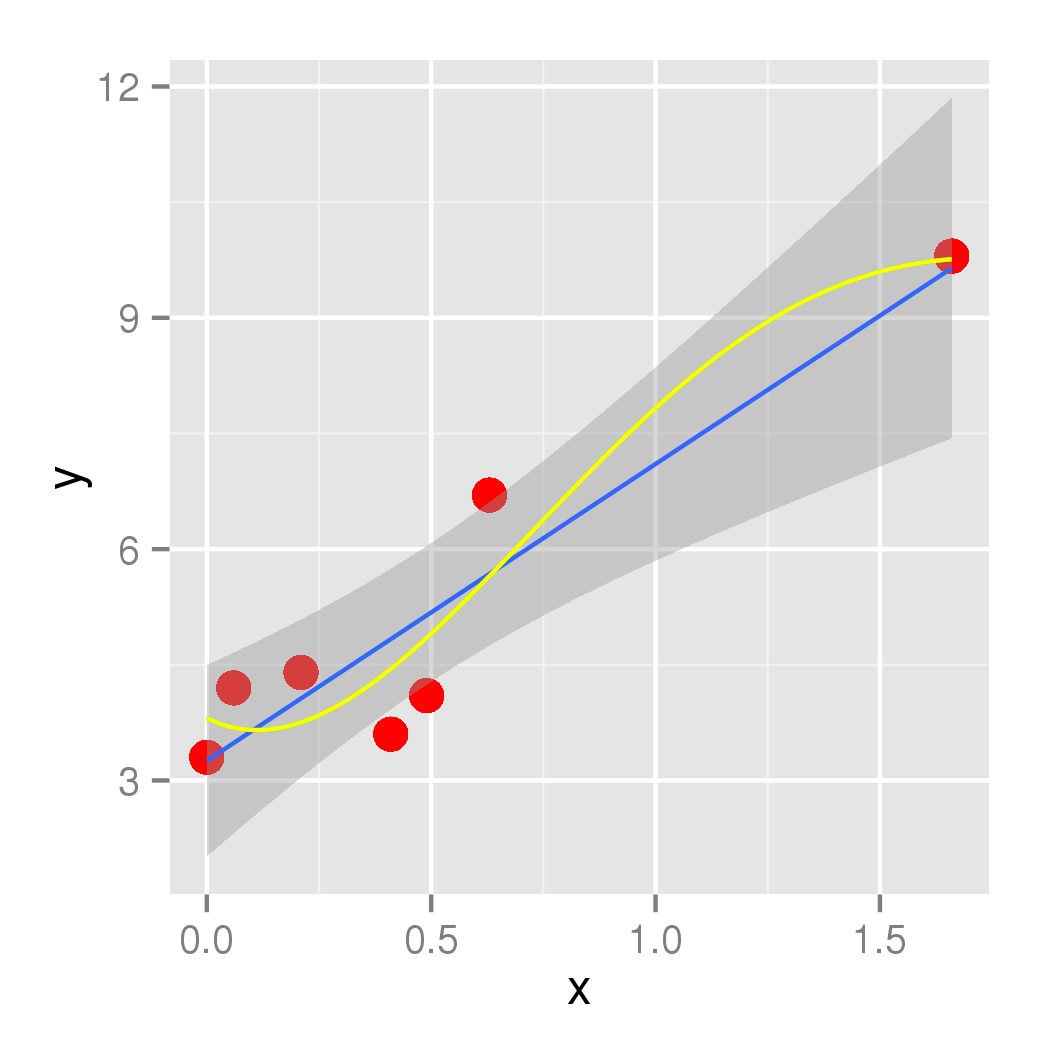Вы можете настроить пенальти, и grid, места, где отклонения оштрафованный.
источник Ott Toomets не работал для меня, были некоторые ошибки. Вот исправленная версия (без использования ggplot2):
library(maxLik)
x <- c(0, 6, 21, 41, 49, 63, 166)/100
y <- c(3.3, 4.2, 4.4, 3.6, 4.1, 6.7, 9.8)
df <- data.frame(x, y)
polyf <- function(par, x=df$x) {
## the polynomial function
par[1]*x + par[2]*x^2 + par[3]*x^3 + par[4]*x^4 + par[5]
}
quarticP <- function(x) {
polyf(par, x)
}
## a evenly distributed set of points, penalize deviations on these
grid <- seq(range(df$x)[1], range(df$x)[2], length=10)
objectiveF <- function(par, kappa=0) {
## Calculate penalized sum of squares: penalty for deviating from linear
## prediction
PSS <- sum((df$y - polyf(par))^2) + kappa*(pred1 - polyf(par, x=grid))^2
-PSS
}
plot(x,y, ylim=c(0,10))
## first compute linear model prediction
res1 <- lm(y~x, data=df)
pred1 <- predict(res1, newdata=data.frame(x=grid))
coefs = coef(res1)
names(coefs) = NULL
constant = coefs[1]
xCoefficient = coefs[2]
par = c(xCoefficient,0,0,0,constant)
curve(quarticP, from=0, to=2, col="black", add=T)
## non-penalized function
res <- maxBFGS(objectiveF, start=c(0,0,0,0,0))
par <- coef(res)
curve(quarticP, from=0, to=2, col="red", add=T)
## penalty
res2 <- maxBFGS(objectiveF, start=c(0,0,0,0,0), kappa=0.5)
par <- coef(res2)
curve(quarticP, from=0, to=2, col="green", add=T)