Получение несжатого открытого ключа ECDSA из сжатого

в настоящее время я пытаюсь получить биткойн несжатый открытый ключ ECDSA из сжатого.

по этому ссылка на Bitcoin wiki, это можно сделать так... Но как?

чтобы дать вам более подробную информацию: на данный момент у меня есть сжатые ключи (длиной 33 байта), собранные в сети bitcoin.

они имеют следующий формат: . Оттуда я хотел бы получить несжатый ключ (Длиной 65 байт), чей формат:

по этому другая ссылка на Bitcoin wiki, это должно быть так просто, как решить уравнение:

Y^2 = X^3 + 7

однако я не могу туда добраться. Мое значение для Y просто далеко. Вот мой код (значение для открытого ключа происходит от Bitcoin wiki пример):

import binascii
from decimal import *

expected_uncompressed_key_hex = '0450863AD64A87AE8A2FE83C1AF1A8403CB53F53E486D8511DAD8A04887E5B23522CD470243453A299FA9E77237716103ABC11A1DF38855ED6F2EE187E9C582BA6'
expected_y_hex = expected_uncompressed_key_hex[-64:]
expected_y_dec = int(expected_y_hex, 16)
x_hex = expected_uncompressed_key_hex[2:66]
if expected_y_dec % 2 == 0:
    prefix = "02"
else:
    prefix = "03"

artificial_compressed_key = prefix + x_hex

getcontext().prec = 500
test_dec = Decimal(int(x_hex, 16))
y_square_dec = test_dec**3 + 7
if prefix == "02":
    y_dec = - Decimal(y_square_dec).sqrt()
else:
    y_dec = Decimal(y_square_dec).sqrt()

computed_y_hex = hex(int(y_dec))
computed_uncompressed_key = "04" + x + computed_y_hex

для информации, мои выходы являются:

computed_y_hex = '0X2D29684BD207BF6D809F7D0EB78E4FD61C3C6700E88AB100D1075EFA8F8FD893080F35E6C7AC2E2214F8F4D088342951'
expected_y_hex = '2CD470243453A299FA9E77237716103ABC11A1DF38855ED6F2EE187E9C582BA6'

Спасибо за вашу помощь!

8
bitcoin ecdsa public-key python

2 ответов

вам нужно рассчитать в поле 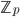Z_p, что в основном означает, что вы должны уменьшить свое число до остатка после деления с p после каждого вычисления. Вычисление это называется взятием по модулю и записывается как % p в python.

возведение в степень в этой области может быть сделано более эффективно, чем наивный способ просто умножения и уменьшения во много раз. Это называется модульным возведением в степень. Встроенная функция экспоненции Python pow (n,e, p) может принимать позаботься об этом.

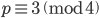
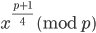
оставшаяся проблема заключается в том, чтобы найти квадратный корень. К счастью, secp256k1 выбран особым образом (p%4=3), так что взять квадратные корни легко: квадратный корень из x равен x^((p+1)/4)%p.

таким образом, упрощенная версия кода выглядит так:

import binascii

p_hex = 'FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F'
p = int(p_hex, 16)
compressed_key_hex = '0250863AD64A87AE8A2FE83C1AF1A8403CB53F53E486D8511DAD8A04887E5B2352'
x_hex = compressed_key_hex[2:66]
x = int(x_hex, 16)
prefix = compressed_key_hex[0:2]

y_square = (pow(x, 3, p)  + 7) % p
y_square_square_root = pow(y_square, (p+1)/4, p)
if (prefix == "02" and y_square_square_root & 1) or (prefix == "03" and not y_square_square_root & 1):
    y = (-y_square_square_root) % p
else:
    y = y_square_square_root

computed_y_hex = format(y, '064x')
computed_uncompressed_key = "04" + x_hex + computed_y_hex

print computed_uncompressed_key
4

поле эллиптической кривой не находится над полем действительных чисел. Это над конечным полем по модулю некоторого простого.

для Secp256k1 простое p = 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1.

таким образом: y^2= (x^3) + 7 (mod p)

нет прямого способа решить уравнение, вам нужно будет использовать алгоритм Cipolla:https://en.wikipedia.org/wiki/Cipolla%27s_algorithm

3