Получение powerset набора в Java
powerset {1, 2, 3} - это:
{{}, {2}, {3}, {2, 3}, {1, 2}, {1, 3}, {1, 2, 3}, {1}}
допустим, у меня есть Set в Java:
Set<Integer> mySet = new HashSet<Integer>();
mySet.add(1);
mySet.add(2);
mySet.add(3);
Set<Set<Integer>> powerSet = getPowerset(mySet);
Как написать функцию getPowerset, с наилучшим возможным порядком сложности? (Я думаю, что это может быть O(2^n).)
25 ответов
Да, это O(2^n) действительно, так как вам нужно генерировать, ну,2^n возможных комбинаций. Вот рабочая реализация, использующая дженерики и наборы:
public static <T> Set<Set<T>> powerSet(Set<T> originalSet) {
Set<Set<T>> sets = new HashSet<Set<T>>();
if (originalSet.isEmpty()) {
sets.add(new HashSet<T>());
return sets;
}
List<T> list = new ArrayList<T>(originalSet);
T head = list.get(0);
Set<T> rest = new HashSet<T>(list.subList(1, list.size()));
for (Set<T> set : powerSet(rest)) {
Set<T> newSet = new HashSet<T>();
newSet.add(head);
newSet.addAll(set);
sets.add(newSet);
sets.add(set);
}
return sets;
}
и тест, учитывая ваш пример ввода:
Set<Integer> mySet = new HashSet<Integer>();
mySet.add(1);
mySet.add(2);
mySet.add(3);
for (Set<Integer> s : SetUtils.powerSet(mySet)) {
System.out.println(s);
}
на самом деле, я написал код, который делает то, что вы просите за O(1). Вопрос в том, что вы планируете do С набором далее. Если вы просто собираетесь позвонить size() на нем, Это O (1), но если вы собираетесь повторить его, это очевидно O(2^n).
contains() будет O(n), etc.
вам действительно это нужно?
EDIT:
этот код теперь доступен в Guava, выставленный через метод Sets.powerSet(set).
вот решение, в котором я использую генератор, преимущество в том, что весь набор мощности никогда не сохраняется сразу... Таким образом, вы можете перебирать его один за другим без необходимости хранить его в памяти. Хотелось бы думать, что это лучший вариант... Обратите внимание, что сложность одинакова, O (2^n), но требования к памяти уменьшаются (при условии, что сборщик мусора ведет себя! ;))
/**
*
*/
package org.mechaevil.util.Algorithms;
import java.util.BitSet;
import java.util.Iterator;
import java.util.Set;
import java.util.TreeSet;
/**
* @author st0le
*
*/
public class PowerSet<E> implements Iterator<Set<E>>,Iterable<Set<E>>{
private E[] arr = null;
private BitSet bset = null;
@SuppressWarnings("unchecked")
public PowerSet(Set<E> set)
{
arr = (E[])set.toArray();
bset = new BitSet(arr.length + 1);
}
@Override
public boolean hasNext() {
return !bset.get(arr.length);
}
@Override
public Set<E> next() {
Set<E> returnSet = new TreeSet<E>();
for(int i = 0; i < arr.length; i++)
{
if(bset.get(i))
returnSet.add(arr[i]);
}
//increment bset
for(int i = 0; i < bset.size(); i++)
{
if(!bset.get(i))
{
bset.set(i);
break;
}else
bset.clear(i);
}
return returnSet;
}
@Override
public void remove() {
throw new UnsupportedOperationException("Not Supported!");
}
@Override
public Iterator<Set<E>> iterator() {
return this;
}
}
чтобы вызвать его, используйте этот шаблон:
Set<Character> set = new TreeSet<Character> ();
for(int i = 0; i < 5; i++)
set.add((char) (i + 'A'));
PowerSet<Character> pset = new PowerSet<Character>(set);
for(Set<Character> s:pset)
{
System.out.println(s);
}
это из моей библиотеки проекта Эйлера... :)
Если n Math.pow() и массивы для масок, но почему-то пользователи Java их боятся...
List<T> list = new ArrayList<T>(originalSet);
int n = list.size();
Set<Set<T>> powerSet = new HashSet<Set<T>>();
for( long i = 0; i < (1 << n); i++) {
Set<T> element = new HashSet<T>();
for( int j = 0; j < n; j++ )
if( (i >> j) % 2 == 1 ) element.add(list.get(j));
powerSet.add(element);
}
return powerSet;
здесь представляет собой учебник, описывающий именно то, что вы хотите, включая код. Вы правы в том, что сложность равна O (2^n).
Я придумал другое решение, основанное на идеях @Harry He. Вероятно, не самый элегантный, но здесь он идет, как я понимаю:
возьмем классический простой пример PowerSet из S P(S) = {{1},{2},{3}}. Мы знаем, что формула для получения числа подмножеств равна 2^n (7 + пустое множество). Например 2^3 = 8 подмножеств.
чтобы найти каждое подмножество, нам нужно преобразовать 0-7 десятичное в двоичное представление, показанное в таблице преобразования ниже:
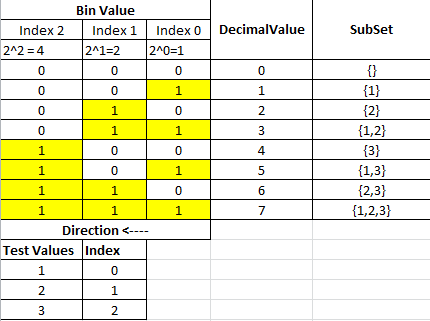
Если мы пересечем таблицу строка за строкой, каждая строка приведет к подмножеству, и значения каждого подмножества будут поступать из включенных битов.
каждый столбец в разделе Bin Value соответствует позиции индекса в исходном входном наборе.
вот мой код:
public class PowerSet {
/**
* @param args
*/
public static void main(String[] args) {
PowerSet ps = new PowerSet();
Set<Integer> set = new HashSet<Integer>();
set.add(1);
set.add(2);
set.add(3);
for (Set<Integer> s : ps.powerSet(set)) {
System.out.println(s);
}
}
public Set<Set<Integer>> powerSet(Set<Integer> originalSet) {
// Original set size e.g. 3
int size = originalSet.size();
// Number of subsets 2^n, e.g 2^3 = 8
int numberOfSubSets = (int) Math.pow(2, size);
Set<Set<Integer>> sets = new HashSet<Set<Integer>>();
ArrayList<Integer> originalList = new ArrayList<Integer>(originalSet);
for (int i = 0; i < numberOfSubSets; i++) {
// Get binary representation of this index e.g. 010 = 2 for n = 3
String bin = getPaddedBinString(i, size);
//Get sub-set
Set<Integer> set = getSet(bin, originalList));
sets.add(set);
}
return sets;
}
//Gets a sub-set based on the binary representation. E.g. for 010 where n = 3 it will bring a new Set with value 2
private Set<Integer> getSet(String bin, List<Integer> origValues){
Set<Integer> result = new HashSet<Integer>();
for(int i = bin.length()-1; i >= 0; i--){
//Only get sub-sets where bool flag is on
if(bin.charAt(i) == '1'){
int val = origValues.get(i);
result.add(val);
}
}
return result;
}
//Converts an int to Bin and adds left padding to zero's based on size
private String getPaddedBinString(int i, int size) {
String bin = Integer.toBinaryString(i);
bin = String.format("%0" + size + "d", Integer.parseInt(bin));
return bin;
}
}
Если вы используете Коллекции Eclipse (ранее коллекции GS), вы можете использовать powerSet() метод для всех SetIterables.
MutableSet<Integer> set = UnifiedSet.newSetWith(1, 2, 3);
System.out.println("powerSet = " + set.powerSet());
// prints: powerSet = [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
Примечание: я коммиттер для коллекций Eclipse.
Я искал решение, которое не было таким огромным, как те, которые размещены здесь. Это нацелено на Java 7, поэтому для версий 5 и 6 потребуется несколько паст.
Set<Set<Object>> powerSetofNodes(Set<Object> orig) {
Set<Set<Object>> powerSet = new HashSet<>(),
runSet = new HashSet<>(),
thisSet = new HashSet<>();
while (powerSet.size() < (Math.pow(2, orig.size())-1)) {
if (powerSet.isEmpty()) {
for (Object o : orig) {
Set<Object> s = new TreeSet<>();
s.add(o);
runSet.add(s);
powerSet.add(s);
}
continue;
}
for (Object o : orig) {
for (Set<Object> s : runSet) {
Set<Object> s2 = new TreeSet<>();
s2.addAll(s);
s2.add(o);
powerSet.add(s2);
thisSet.add(s2);
}
}
runSet.clear();
runSet.addAll(thisSet);
thisSet.clear();
}
powerSet.add(new TreeSet());
return powerSet;
вот пример кода для проверки:
Set<Object> hs = new HashSet<>();
hs.add(1);
hs.add(2);
hs.add(3);
hs.add(4);
for(Set<Object> s : powerSetofNodes(hs)) {
System.out.println(Arrays.toString(s.toArray()));
}
следующее решение заимствовано из моей книги " Кодирование Интервью: Вопросы, Анализ И Решения":
выбираются некоторые целые числа в массиве, которые составляют комбинацию. Используется набор битов, где каждый бит обозначает целое число в массиве. Если i-й символ выбирается для комбинации,i-й бит равен 1; в противном случае-0. Например, три бита используются для комбинаций массива [1, 2, 3]. Если первые два целых числа 1 и 2 выбираются для составления комбинации [1, 2], соответствующие биты {1, 1, 0}. Аналогично, биты, соответствующие другой комбинации [1, 3], являются {1, 0, 1}. Мы можем получить все комбинации массива с длиной n если мы сможем получить все возможные комбинации n бит.
число состоит из набора битов. Все возможные комбинации n биты соответствуют номерам от 1 до 2^n-1. Поэтому каждое число в диапазоне от 1 до 2^n-1 соответствует комбинации массива с длиной n. Например, число 6 состоит из битов {1, 1, 0}, поэтому первый и второй символы выбираются в массиве [1, 2, 3] для генерации комбинации [1, 2]. Аналогично, число 5 с битами {1, 0, 1} соответствует комбинации [1, 3].
код Java для реализации этого решения выглядит следующим образом:
public static ArrayList<ArrayList<Integer>> powerSet(int[] numbers) {
ArrayList<ArrayList<Integer>> combinations = new ArrayList<ArrayList<Integer>>();
BitSet bits = new BitSet(numbers.length);
do{
combinations.add(getCombination(numbers, bits));
}while(increment(bits, numbers.length));
return combinations;
}
private static boolean increment(BitSet bits, int length) {
int index = length - 1;
while(index >= 0 && bits.get(index)) {
bits.clear(index);
--index;
}
if(index < 0)
return false;
bits.set(index);
return true;
}
private static ArrayList<Integer> getCombination(int[] numbers, BitSet bits){
ArrayList<Integer> combination = new ArrayList<Integer>();
for(int i = 0; i < numbers.length; ++i) {
if(bits.get(i))
combination.add(numbers[i]);
}
return combination;
}
в метод increment увеличивает число, представленное в наборе битов. Алгоритм очищает 1 бит от крайний правый бит до 0 бит не найдено. Затем он ставит правую 0 бит 1. Например, чтобы увеличить число 5 с битами {1, 0, 1}, он очищает 1 бит с правой стороны и устанавливает самый правый 0 бит в 1. Биты становятся {1, 1, 0} для числа 6, которое является результатом увеличения 5 на 1.
некоторые из решений выше страдают, когда размер набора большой, потому что они создают много мусора объектов для сбора и требуют копирования данных. Как этого избежать? Мы можем воспользоваться тем фактом, что знаем, насколько большим будет размер результирующего набора (2^n), предварительно распределить такой большой массив и просто добавить его в конец, никогда не копируя.
ускорение быстро растет с n. Я сравнил его с решением Жуана Сильвы выше. На моей машине (все измерения ориентировочное), Н=13 в 5 раз быстрее, где N=14-это 7х, Н=15-это 12-кратный, н=16 составляет 25х, Н=17 составляет 75х, н=18-Это 140x. Так что создание мусора/сбор и копирование является доминирующей в то, что иначе, кажется, быть похожими большой-вывода.
предварительное распределение массива в начале кажется выигрышем по сравнению с динамическим его ростом. При n=18 динамический рост занимает примерно в два раза больше времени.
public static <T> List<List<T>> powerSet(List<T> originalSet) {
// result size will be 2^n, where n=size(originalset)
// good to initialize the array size to avoid dynamic growing
int resultSize = (int) Math.pow(2, originalSet.size());
// resultPowerSet is what we will return
List<List<T>> resultPowerSet = new ArrayList<List<T>>(resultSize);
// Initialize result with the empty set, which powersets contain by definition
resultPowerSet.add(new ArrayList<T>(0));
// for every item in the original list
for (T itemFromOriginalSet : originalSet) {
// iterate through the existing powerset result
// loop through subset and append to the resultPowerset as we go
// must remember size at the beginning, before we append new elements
int startingResultSize = resultPowerSet.size();
for (int i=0; i<startingResultSize; i++) {
// start with an existing element of the powerset
List<T> oldSubset = resultPowerSet.get(i);
// create a new element by adding a new item from the original list
List<T> newSubset = new ArrayList<T>(oldSubset);
newSubset.add(itemFromOriginalSet);
// add this element to the result powerset (past startingResultSize)
resultPowerSet.add(newSubset);
}
}
return resultPowerSet;
}
вот простое итеративное решение O(2^n):
public static Set<Set<Integer>> powerSet(List<Integer> intList){
Set<Set<Integer>> result = new HashSet();
result.add(new HashSet());
for (Integer i : intList){
Set<Set<Integer>> temp = new HashSet();
for(Set<Integer> intSet : result){
intSet = new HashSet(intSet);
intSet.add(i);
temp.add(intSet);
}
result.addAll(temp);
}
return result;
}
import java.util.Set;
import com.google.common.collect.*;
Set<Set<Integer>> sets = Sets.powerSet(ImmutableSet.of(1, 2, 3));
Если S-конечное множество С N элементами, то степенное множество S содержит 2^N элементов. Время для простого перечисления элементов powerset равно 2^N, поэтому O(2^N) является нижней границей временной сложности (жадно) построения powerset.
проще говоря, любое вычисление, которое включает в себя создание powersets, не будет масштабироваться для больших значений N. никакой умный алгоритм вам не поможет ... помимо избежания необходимости создания powersets!
один из способов без рекурсии заключается в следующем: использовать двоичную маску и сделайте все возможные сочетания.
public HashSet<HashSet> createPowerSet(Object[] array)
{
HashSet<HashSet> powerSet=new HashSet();
boolean[] mask= new boolean[array.length];
for(int i=0;i<Math.pow(2, array.length);i++)
{
HashSet set=new HashSet();
for(int j=0;j<mask.length;j++)
{
if(mask[i])
set.add(array[j]);
}
powerSet.add(set);
increaseMask(mask);
}
return powerSet;
}
public void increaseMask(boolean[] mask)
{
boolean carry=false;
if(mask[0])
{
mask[0]=false;
carry=true;
}
else
mask[0]=true;
for(int i=1;i<mask.length;i++)
{
if(mask[i]==true && carry==true)
mask[i]=false;
else if (mask[i]==false && carry==true)
{
mask[i]=true;
carry=false;
}
else
break;
}
}
:
вход: Set [], set_size 1. Получить размер power set powet_set_size = pow(2, set_size) 2 Цикл для счетчика от 0 до pow_set_size (A) цикл для i = 0 для set_size (i) если установлен I-й бит в счетчике Вывести I-й элемент из множества для этого подмножества (b) печать разделителя для подмножеств, т. е. newline
#include <stdio.h>
#include <math.h>
void printPowerSet(char *set, int set_size)
{
/*set_size of power set of a set with set_size
n is (2**n -1)*/
unsigned int pow_set_size = pow(2, set_size);
int counter, j;
/*Run from counter 000..0 to 111..1*/
for(counter = 0; counter < pow_set_size; counter++)
{
for(j = 0; j < set_size; j++)
{
/* Check if jth bit in the counter is set
If set then pront jth element from set */
if(counter & (1<<j))
printf("%c", set[j]);
}
printf("\n");
}
}
/*Driver program to test printPowerSet*/
int main()
{
char set[] = {'a','b','c'};
printPowerSet(set, 3);
getchar();
return 0;
}Это мое рекурсивное решение, которое может получить набор мощности любого набора с помощью Java Generics. Его основная идея состоит в том, чтобы объединить головку входного массива со всеми возможными решениями остальной части массива следующим образом.
import java.util.LinkedHashSet;
import java.util.Set;
public class SetUtil {
private static<T> Set<Set<T>> combine(T head, Set<Set<T>> set) {
Set<Set<T>> all = new LinkedHashSet<>();
for (Set<T> currentSet : set) {
Set<T> outputSet = new LinkedHashSet<>();
outputSet.add(head);
outputSet.addAll(currentSet);
all.add(outputSet);
}
all.addAll(set);
return all;
}
//Assuming that T[] is an array with no repeated elements ...
public static<T> Set<Set<T>> powerSet(T[] input) {
if (input.length == 0) {
Set <Set<T>>emptySet = new LinkedHashSet<>();
emptySet.add(new LinkedHashSet<T>());
return emptySet;
}
T head = input[0];
T[] newInputSet = (T[]) new Object[input.length - 1];
for (int i = 1; i < input.length; ++i) {
newInputSet[i - 1] = input[i];
}
Set<Set<T>> all = combine(head, powerSet(newInputSet));
return all;
}
public static void main(String[] args) {
Set<Set<Integer>> set = SetUtil.powerSet(new Integer[] {1, 2, 3, 4, 5, 6});
System.out.println(set);
}
}
это будет выход:
[[1, 2, 3, 4, 5, 6], [1, 2, 3, 4, 5], [1, 2, 3, 4, 6], [1, 2, 3, 4], [1, 2, 3, 5, 6], [1, 2, 3, 5], [1, 2, 3, 6], [1, 2, 3], [1, 2, 4, 5, 6], [1, 2, 4, 5], [1, 2, 4, 6], [1, 2, 4], [1, 2, 5, 6], [1, 2, 5], [1, 2, 6], [1, 2], [1, 3, 4, 5, 6], [1, 3, 4, 5], [1, 3, 4, 6], [1, 3, 4], [1, 3, 5, 6], [1, 3, 5], [1, 3, 6], [1, 3], [1, 4, 5, 6], [1, 4, 5], [1, 4, 6], [1, 4], [1, 5, 6], [1, 5], [1, 6], [1], [2, 3, 4, 5, 6], [2, 3, 4, 5], [2, 3, 4, 6], [2, 3, 4], [2, 3, 5, 6], [2, 3, 5], [2, 3, 6], [2, 3], [2, 4, 5, 6], [2, 4, 5], [2, 4, 6], [2, 4], [2, 5, 6], [2, 5], [2, 6], [2], [3, 4, 5, 6], [3, 4, 5], [3, 4, 6], [3, 4], [3, 5, 6], [3, 5], [3, 6], [3], [4, 5, 6], [4, 5], [4, 6], [4], [5, 6], [5], [6], []]
Это мой подход с лямбдами.
public static <T> Set<Set<T>> powerSet(T[] set) {
return IntStream
.range(0, (int) Math.pow(2, set.length))
.parallel() //performance improvement
.mapToObj(e -> IntStream.range(0, set.length).filter(i -> (e & (0b1 << i)) != 0).mapToObj(i -> set[i]).collect(Collectors.toSet()))
.map(Function.identity())
.collect(Collectors.toSet());
}
или параллельно (см. комментарий parallel ()):
размер входного набора: 18
логические процессоры: 8 à 3,4 ГГц
повышение производительности: 30%
подмножество t-это любое множество, которое может быть сделано путем удаления нуля или более элементов t. Подмножество withoutFirst добавляет подмножества t, в которых отсутствует первый элемент, а цикл for будет иметь дело с добавлением подмножеств с первым элементом. Например, если t содержит элементы ["1", "2", "3"], missingFirst добавит [[""], ["2"], ["3"], ["2","3"]] и цикл for будет вставлять "1" перед этим элементом и добавлять его в newSet. Так что мы закончим [[""], ["1"], ["2"], ["3"], ["1", "2"], ["1", "3"], ["2","3"], ["1", "2", "3"]].
public static Set<Set<String>> allSubsets(Set<String> t) {
Set<Set<String>> powerSet = new TreeSet<>();
if(t.isEmpty()) {
powerSet.add(new TreeSet<>());
return powerSet;
}
String first = t.get(0);
Set<Set<String>> withoutFirst = allSubsets(t.subSet(1, t.size()));
for (List<String> 1st : withoutFirst) {
Set<String> newSet = new TreeSet<>();
newSet.add(first);
newSet.addAll(lst);
powerSet.add(newSet);
}
powerSet.addAll(withoutFirst);
return powerSet;
}
// input: S
// output: P
// S = [1,2]
// P = [], [1], [2], [1,2]
public static void main(String[] args) {
String input = args[0];
String[] S = input.split(",");
String[] P = getPowerSet(S);
if (P.length == Math.pow(2, S.length)) {
for (String s : P) {
System.out.print("[" + s + "],");
}
} else {
System.out.println("Results are incorrect");
}
}
private static String[] getPowerSet(String[] s) {
if (s.length == 1) {
return new String[] { "", s[0] };
} else {
String[] subP1 = getPowerSet(Arrays.copyOfRange(s, 1, s.length));
String[] subP2 = new String[subP1.length];
for (int i = 0; i < subP1.length; i++) {
subP2[i] = s[0] + subP1[i];
}
String[] P = new String[subP1.length + subP2.length];
System.arraycopy(subP1, 0, P, 0, subP1.length);
System.arraycopy(subP2, 0, P, subP1.length, subP2.length);
return P;
}
}
недавно мне пришлось использовать что-то вроде этого, но нужны были самые маленькие подсписки (с 1 элементом, затем 2 элемента, ...) сначала. Я не хотел включать ни пустой, ни весь список. Кроме того, мне не нужен был список всех возвращенных подсписков, мне просто нужно было сделать некоторые вещи с каждым.
хотел сделать это без рекурсии, и придумал следующее (С "делать вещи" объединяются в функциональный интерфейс):
@FunctionalInterface interface ListHandler<T> {
void handle(List<T> list);
}
public static <T> void forAllSubLists(final List<T> list, ListHandler handler) {
int ll = list.size(); // Length of original list
int ci[] = new int[ll]; // Array for list indices
List<T> sub = new ArrayList<>(ll); // The sublist
List<T> uml = Collections.unmodifiableList(sub); // For passing to handler
for (int gl = 1, gm; gl <= ll; gl++) { // Subgroup length 1 .. n-1
gm = 0; ci[0] = -1; sub.add(null); // Some inits, and ensure sublist is at least gl items long
do {
ci[gm]++; // Get the next item for this member
if (ci[gm] > ll - gl + gm) { // Exhausted all possibilities for this position
gm--; continue; // Continue with the next value for the previous member
}
sub.set(gm, list.get(ci[gm])); // Set the corresponding member in the sublist
if (gm == gl - 1) { // Ok, a sublist with length gl
handler.handle(uml); // Handle it
} else {
ci[gm + 1] = ci[gm]; // Starting value for next member is this
gm++; // Continue with the next member
}
} while (gm >= 0); // Finished cycling through all possibilities
} // Next subgroup length
}
таким образом, это также легко ограничить его подсписков специфических длин.
еще один пример реализации:
public static void main(String args[])
{
int[] arr = new int[]{1,2,3,4};
// Assuming that number of sets are in integer range
int totalSets = (int)Math.pow(2,arr.length);
for(int i=0;i<totalSets;i++)
{
String binaryRep = Integer.toBinaryString(i);
for(int j=0;j<binaryRep.length();j++)
{
int index=binaryRep.length()-1-j;
if(binaryRep.charAt(index)=='1')
System.out.print(arr[j] +" ");
}
System.out.println();
}
}
public class PowerSet {
public static List<HashSet<Integer>> powerset(int[] a) {
LinkedList<HashSet<Integer>> sets = new LinkedList<HashSet<Integer>>();
int n = a.length;
for (int i = 0; i < 1 << n; i++) {
HashSet<Integer> set = new HashSet<Integer>();
for (int j = 0; j < n; j++) {
if ((1 << j & i) > 0)
set.add(a[j]);
}
sets.add(set);
}
return sets;
}
public static void main(String[] args) {
List<HashSet<Integer>> sets = PowerSet.powerset(new int[]{ 1, 2, 3 });
for (HashSet<Integer> set : sets) {
for (int i : set)
System.out.print(i);
System.out.println();
}
}
}
еще одно решение - с java8 + streaming api Он ленив и упорядочен, поэтому он возвращает правильные подмножества, когда он используется с " limit ()".
public long bitRangeMin(int size, int bitCount){
BitSet bs = new BitSet(size);
bs.set(0, bitCount);
return bs.toLongArray()[0];
}
public long bitRangeMax(int size, int bitCount){
BitSet bs = BitSet.valueOf(new long[]{0});
bs.set(size - bitCount, size);
return bs.toLongArray()[0];
}
public <T> Stream<List<T>> powerSet(Collection<T> data)
{
List<T> list = new LinkedHashSet<>(data).stream().collect(Collectors.toList());
Stream<BitSet> head = LongStream.of(0).mapToObj( i -> BitSet.valueOf(new long[]{i}));
Stream<BitSet> tail = IntStream.rangeClosed(1, list.size())
.boxed()
.flatMap( v1 -> LongStream.rangeClosed( bitRangeMin(list.size(), v1), bitRangeMax(list.size(), v1))
.mapToObj(v2 -> BitSet.valueOf(new long[]{v2}))
.filter( bs -> bs.cardinality() == v1));
return Stream.concat(head, tail)
.map( bs -> bs
.stream()
.mapToObj(list::get)
.collect(Collectors.toList()));
}
и код клиента
@Test
public void testPowerSetOfGivenCollection(){
List<Character> data = new LinkedList<>();
for(char i = 'a'; i < 'a'+5; i++ ){
data.add(i);
}
powerSet(data)
.limit(9)
.forEach(System.out::print);
}
/ * печать: [] [a][b][c][d] [e] [a, b] [a, c] [b, c]*/
мы могли бы написать набор мощности с или без использования рекурсии. Вот попытка без рекурсии:
public List<List<Integer>> getPowerSet(List<Integer> set) {
List<List<Integer>> powerSet = new ArrayList<List<Integer>>();
int max = 1 << set.size();
for(int i=0; i < max; i++) {
List<Integer> subSet = getSubSet(i, set);
powerSet.add(subSet);
}
return powerSet;
}
private List<Integer> getSubSet(int p, List<Integer> set) {
List<Integer> subSet = new ArrayList<Integer>();
int position = 0;
for(int i=p; i > 0; i >>= 1) {
if((i & 1) == 1) {
subSet.add(set.get(position));
}
position++;
}
return subSet;
}
здесь для генерации набора мощности. Идея первая = S[0] и меньших наборов S[1,...n].
вычислить все подмножества smallerSet и поместить их в allsubsets.
для каждого подмножества в allsubsets клонируйте его и добавьте сначала в подмножество.
ArrayList<ArrayList<Integer>> getSubsets(ArrayList<Integer> set, int index){
ArrayList<ArrayList<Integer>> allsubsets;
if(set.size() == index){
allsubsets = new ArrayList<ArrayList<Integer>>();
allsubsets.add(new ArrayList<Integer>()); // the empty set
}else{
allsubsets = getSubsets(set, index+1);
int item = set.get(index);
ArrayList<ArrayList<Integer>> moresubsets = new ArrayList<ArrayList<Integer>>();
for(ArrayList<Integer> subset: allsubsets){
ArrayList<Integer> newsubset = new ArrayList<Integer>();
newsubset.addAll(subset);
newsubset.add(item);
moresubsets.add(newsubset);
}
moresubsets.addAll(moresubsets);
}
return allsubsets;
}
