Понимание Функции Ackermann
Мне трудно понять, как работает функция Ackermann. Я думаю, что мое понимание рекурсии ущербно?
вот код в Python:
def naive_ackermann(m, n):
global calls
calls += 1
if m == 0:
return n + 1
elif n == 0:
return naive_ackermann(m - 1, 1)
else:
return naive_ackermann(m - 1, naive_ackermann(m, n - 1))
Если я выполняю вызов функции naive_ackermann (3,4), как и почему я получаю 125?
комментарии будут оценены.
спасибо
6 ответов
вычисление A (3,4) не так просто или коротко, как может показаться сначала из небольших значений аргументов. Сложность (#итерационных шагов) функции Аккермана растет очень быстро с ее аргументами, как и вычисляемый результат.
вот определение функции Аккермана от Википедия:
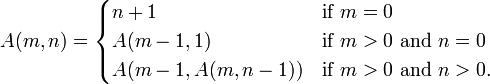
Как вы можете видеть, на каждой итерации значение m уменьшается пока не достигнет 0 в чем будет последний шаг, в какой момент конечное значение n (+1) дает вам ответ. Поэтому для ответа, вам нужно только проследить, как n изменения по мере прохождения рекурсивных итераций. Почему функция Аккермана растет так быстро, вы можете взглянуть на этой подраздел Вики.
Как уже упоминал Джоран Бисли,A (3,4) действительно 125, а написано в Википедии. Однако процесс получения этого результата не очень короткий. На самом деле, как я выяснил, требуется вычислить рекурсией 315 Ackermann значения функции, чтобы получить A (3,4), количество требуемых итераций примерно пропорционально этому.
Если вы все еще хотите визуализировать, как этот результат достигается, вы можете взглянуть на на этой странице, который анимирует вычисление каждого шага рекурсии. Но предупреждаю, что ... --30-->A (3,4) потребуется вечность, чтобы закончить анимацию, но, по крайней мере, вы могли бы получить некоторое представление о процессе с меньшими аргументами.
вот версия, которая печатает объяснение:
def A(m, n, s="%s"):
print s % ("A(%d,%d)" % (m, n))
if m == 0:
return n + 1
if n == 0:
return A(m - 1, 1, s)
n2 = A(m, n - 1, s % ("A(%d,%%s)" % (m - 1)))
return A(m - 1, n2, s)
print A(2,2)
с аргументами 2,2 вывод таков. (С 3,4 это становится уже немного слишком)
A(2,2)
A(1,A(2,1))
A(1,A(1,A(2,0)))
A(1,A(1,A(1,1)))
A(1,A(1,A(0,A(1,0))))
A(1,A(1,A(0,A(0,1))))
A(1,A(1,A(0,2)))
A(1,A(1,3))
A(1,A(0,A(1,2)))
A(1,A(0,A(0,A(1,1))))
A(1,A(0,A(0,A(0,A(1,0)))))
A(1,A(0,A(0,A(0,A(0,1)))))
A(1,A(0,A(0,A(0,2))))
A(1,A(0,A(0,3)))
A(1,A(0,4))
A(1,5)
A(0,A(1,4))
A(0,A(0,A(1,3)))
A(0,A(0,A(0,A(1,2))))
A(0,A(0,A(0,A(0,A(1,1)))))
A(0,A(0,A(0,A(0,A(0,A(1,0))))))
A(0,A(0,A(0,A(0,A(0,A(0,1))))))
A(0,A(0,A(0,A(0,A(0,2)))))
A(0,A(0,A(0,A(0,3))))
A(0,A(0,A(0,4)))
A(0,A(0,5))
A(0,6)
7
ackerman(3,4)
=ackerman(2,ackerman(3,3)) = ackerman(2,61) #ackerman(3,3) = 61 ...
=ackerman(1,ackerman(2,60)) = ackerman (1,123) #ackerman(2,60) = 123...
=ackerman(0,ackerman(1,122)) = ackerman (0,124) #ackerman(1,122) = 124...
= 124+1 = 125
посмотреть http://goo.gl/jDDEA здесь визуализировать ackerman(2,3) ( Это было слишком долго, чтобы визуализировать 3,4)
вот очень хорошее описание того, что это такое, для чего это и его место в теории вычислимости http://en.wikipedia.org/wiki/Ackermann_function
вот реализация Java:
/*
* To change this template, choose Tools | Templates
* and open the template in the editor.
*/
package ackerman;
import java.util.Vector;
/**
*
* @author LajosArpad
*/
public class Main {
public static String status = "ackerman(3, 4)";
public static int ackerman(int m, int n)
{
String temp = status.substring(status.lastIndexOf("ackerman"));
while (temp.indexOf("))") >= 0)
{
temp = temp.substring(0, temp.length() - 2);
}
boolean foo = status.indexOf(")") == status.lastIndexOf(")");
String t1 = foo ? "" : status.substring(0, status.lastIndexOf("ackerman") - 1);
String t2 = foo ? "" : status.substring(status.lastIndexOf("ackerman"));
if (t2.length() > 0)
{
t2 = t2.substring(t2.indexOf(")") + 1);
}
if (m == 0)
{
status = t1 + (n + 1) + t2;
System.out.println(" = " + status);
return n + 1;
}
else if (n == 0)
{
status = t1 + "ackerman(" + (m - 1) + ", 1)" + t2;
System.out.println(" = " + status);
return ackerman(m - 1, 1);
}
else
{
status = t1 + " ackerman(" + (m - 1) + ", ackerman(" + m + ", " + (n - 1) + "))" + t2;
System.out.println(" = " + status);
return ackerman(m - 1, ackerman(m, n - 1));
}
}
/**
* @param args the command line arguments
*/
public static void main(String[] args) {
System.out.println(Main.ackerman(3, 4));
// TODO code application logic here
}
}
просто запустите этот код, и вы узнаете, как работает ackerman. Я не свободно владею Python, но я надеюсь, что это не проблема.
def ackermann(m,n):
"""computes the value of the Ackermann function for the input integers m and n.
the Ackermann function being:
A(m,n)=n+1 if m=0
=A(m-1,1) if m>0 and n=1
=A(m-1,A(m,n-1) if m>0 and n>0"""
if m==0:
print (n+1)
return n+1
elif m>0 and n==0:
print ("ackermann(",m-1,",",1,")") #just 2 chk intrmdt val. and no. of steps invlvd.can be dltd if necessary
return ackermann(m-1,1)
elif m>0 and n>0:
print ("Ackermann(",m-1,",","Ackermann(",m,",",n-1,")",")") #just 2 chk intrmdt val. and no. of steps invlvd.can be dltd if necessary
return ackermann(m-1,ackermann(m,n-1))
просто сделайте простую модификацию кода, чтобы программа печатала все шаги, а не только результат. Код должен выглядеть примерно так, как в конце этой страницы. Запустите его (может занять несколько секунд), а затем вы сможете оценить, как вычисляется функция Ackermann.
