Понимание концепции моделей Гауссовой смеси
Я пытаюсь понять GMM, читая источники, доступные в интернете. Я достиг кластеризации с использованием K-Means и видел, как GMM будет сравниваться с K-means.
вот что я понял, пожалуйста, дайте мне знать, если моя концепция неверна:
GMM похож на KNN в том смысле, что кластеризация достигается в обоих случаях. Но в GMM каждый кластер имеет свое собственное независимое среднее и ковариацию. Кроме того, k-means выполняет жесткие назначения точек данных кластеры, тогда как в GMM мы получаем набор независимых гауссовых распределений, и для каждой точки данных у нас есть вероятность того, что она принадлежит одному из распределений.
чтобы лучше понять это, я использовал MatLab для его кодирования и достижения желаемой кластеризации. Я использовал функции SIFT для извлечения функций. И использовали кластеризацию k-means для инициализации значений. (Это из VLFeat документация)
%images is a 459 x 1 cell array where each cell contains the training image
[locations, all_feats] = vl_dsift(single(images{1}), 'fast', 'step', 50); %all_feats will be 128 x no. of keypoints detected
for i=2:(size(images,1))
[locations, feats] = vl_dsift(single(images{i}), 'fast', 'step', 50);
all_feats = cat(2, all_feats, feats); %cat column wise all features
end
numClusters = 50; %Just a random selection.
% Run KMeans to pre-cluster the data
[initMeans, assignments] = vl_kmeans(single(all_feats), numClusters, ...
'Algorithm','Lloyd', ...
'MaxNumIterations',5);
initMeans = double(initMeans); %GMM needs it to be double
% Find the initial means, covariances and priors
for i=1:numClusters
data_k = all_feats(:,assignments==i);
initPriors(i) = size(data_k,2) / numClusters;
if size(data_k,1) == 0 || size(data_k,2) == 0
initCovariances(:,i) = diag(cov(data'));
else
initCovariances(:,i) = double(diag(cov(double((data_k')))));
end
end
% Run EM starting from the given parameters
[means,covariances,priors,ll,posteriors] = vl_gmm(double(all_feats), numClusters, ...
'initialization','custom', ...
'InitMeans',initMeans, ...
'InitCovariances',initCovariances, ...
'InitPriors',initPriors);
на основе вышеизложенного у меня есть means, covariances и priors. Мой главный вопрос, что теперь? Я вроде как заблудился.
и means, covariances векторы каждый из размера 128 x 50. Я ожидал, что они будут 1 x 50 поскольку каждый столбец является кластером, не каждый кластер имеет только одно среднее и ковариацию? (Я знаю, что 128-это функции просеивания, но я ожидал средств и ковариаций).
в k-означает, что я использовал MatLab команда knnsearch(X,Y) который в основном находит ближайшего соседа в X для каждой точки в Y.
Итак, как достичь этого в GMM, я знаю его набор вероятностей, и, конечно, ближайший матч из этой вероятности будет нашим выигрышным кластером. И вот тут я в замешательстве.
Все учебники онлайн научили, как достичь means, covariances значения, но не говорите много о том, как их использовать с точки зрения кластеризации.
спасибо
3 ответов
Я думаю, что это поможет, если вы сначала посмотрите на то, что гмм модель представляет. Я буду использовать функции С Статистика Toolbox, но вы должны быть в состоянии сделать то же самое с помощью VLFeat.
давайте начнем с случая смеси двух 1-мерных нормальных распределений. Каждый Гаусс представлен парой mean и дисперсия. Смесь присваивает вес каждому компонент (предыдущий).
например, давайте смешаем два нормальных распределения с равными весами (p = [0.5; 0.5]), первый центрирован на 0, а второй-на 5 (mu = [0; 5]), а дисперсии равны 1 и 2 соответственно для первого и второго распределений (sigma = cat(3, 1, 2)).
как вы можете видеть ниже, среднее значение эффективно сдвигает распределение, в то время как дисперсия определяет, насколько она широкая/узкая и плоская/заостренная. Приор устанавливает смешивая пропорции для того чтобы получить окончательное совмещенное модель.
% create GMM
mu = [0; 5];
sigma = cat(3, 1, 2);
p = [0.5; 0.5];
gmm = gmdistribution(mu, sigma, p);
% view PDF
ezplot(@(x) pdf(gmm,x));
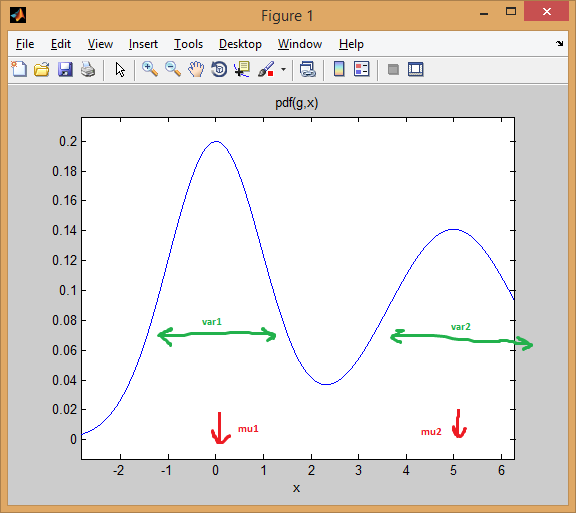
идея кластеризация ЭМ является то, что каждый дистрибутив представляет кластер. Итак, в приведенном выше примере с одномерными данными, если вам был предоставлен экземпляр x = 0.5, мы бы присвоили его как принадлежащий к первому кластеру / режиму с вероятностью 99,5%
>> x = 0.5;
>> posterior(gmm, x)
ans =
0.9950 0.0050 % probability x came from each component
вы можете видеть, как экземпляр хорошо попадает под первую колоколообразную кривую. В то время как если вы возьмете точку посередине, ответ будет больше неоднозначно (точка, присвоенная классу=2, но с гораздо меньшей уверенностью):
>> x = 2.2
>> posterior(gmm, 2.2)
ans =
0.4717 0.5283
те же понятия распространяются на более высокое измерение с многомерные нормальные распределения. В более чем одном измерении матрица ковариации является обобщением дисперсии, чтобы учитывать взаимозависимости между функциями.
вот пример снова со смесью двух распределений MVN в 2-Размеры:
% first distribution is centered at (0,0), second at (-1,3)
mu = [0 0; 3 3];
% covariance of first is identity matrix, second diagonal
sigma = cat(3, eye(2), [5 0; 0 1]);
% again I'm using equal priors
p = [0.5; 0.5];
% build GMM
gmm = gmdistribution(mu, sigma, p);
% 2D projection
ezcontourf(@(x,y) pdf(gmm,[x y]));
% view PDF surface
ezsurfc(@(x,y) pdf(gmm,[x y]));
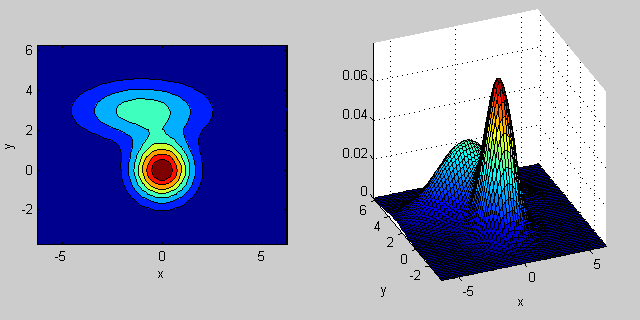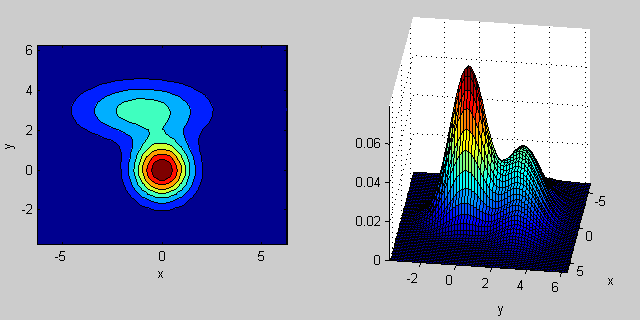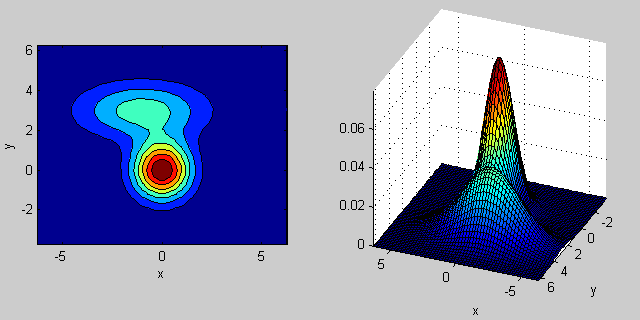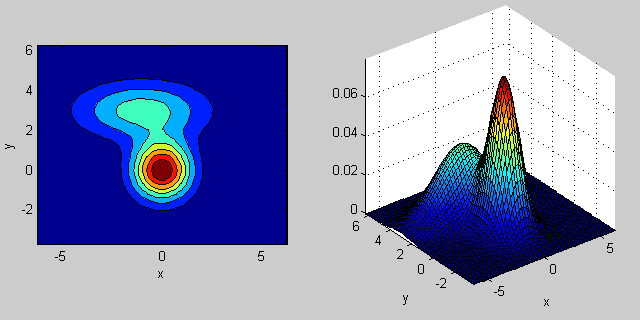
существует некоторая интуиция за тем, как ковариационная матрица влияет на форму совместной функции плотности. Например, в 2D, если матрица диагональна, это означает, что два измерения не меняются. В этом случае PDF будет выглядеть как выровненный по оси эллипс, растянутый по горизонтали или вертикали в соответствии с тем, какое измерение имеет большую дисперсию. Если они равны, то форма представляет собой идеальный круг (распределение распространяется в обоих измерениях с одинаковой скоростью). Наконец, если ковариационная матрица произвольна (не диагональна, но по определению симметрична), то она, вероятно, будет выглядеть как вытянутый эллипс, повернутый под некоторым углом.
таким образом, на предыдущем рисунке вы должны быть в состоянии сказать, что два "бугра" друг от друга и какое индивидуальное распределение каждый представляет. Когда вы идете 3D и более высокие измерения, подумайте об этом как о представлении (hyper-)эллипсоидов in Н-разм.
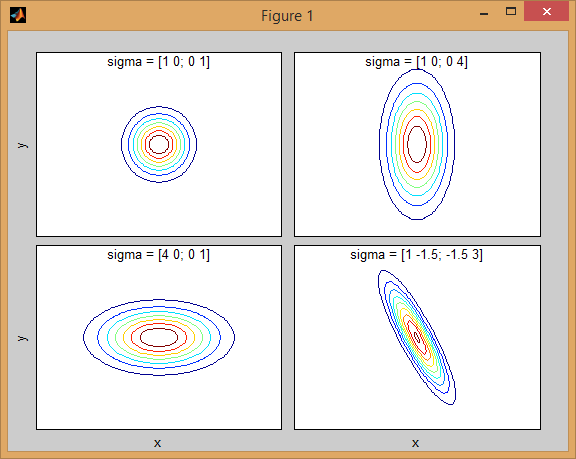
теперь, когда вы выполняете кластеризации используя GMM, цель состоит в том, чтобы найти параметры модели (среднее и ковариацию каждого распределения, а также Приоры), чтобы полученная модель наилучшим образом соответствовала данным. Оценка наилучшего соответствия переводится в максимизация вероятности данных, заданных моделью GMM (это означает, что вы выбираете модель, которая максимизирует Pr(data|model)).
как другие объяснили, это решается итеративно с помощью алгоритм EM; EM начинается с начальной оценки или догадки параметров модели смеси. Он итеративно повторно оценивает экземпляры данных относительно плотности смеси, производимой параметрами. Повторно забитые экземпляры затем используются для обновления оценок параметров. Это повторяется до тех пор, пока алгоритм не сойдется.
к сожалению, алгоритм EM очень чувствителен к инициализации модели, поэтому может потребоваться долгое время сходиться, если вы устанавливаете плохие начальные значения или даже застреваете в локальные оптимумы. Лучший способ инициализации параметров GMM-использовать к-означает как первый шаг (как вы показали в своем коде) и использование среднего/cov этих кластеров для инициализации EM.
как и в других методах кластерного анализа, нам сначала нужно определитесь с количеством кластеров использовать. перекрестная проверка - это надежный способ найти хорошего оценка количества кластеров.
em кластеризация страдает от того, что там много параметров, чтобы соответствовать, и обычно требует много данных и много итераций, чтобы получить хорошие результаты. Неограниченная модель с M-смесями и D-мерными данными включает подгонку D*D*M + D*M + M параметры (M ковариационных матриц каждого размера DxD, плюс M средних векторов длины D, плюс вектор Приоров длины M). Это может быть проблемой для наборов данных с большое количество размеры. Поэтому принято вводить ограничения и предположения, чтобы упростить задачу (своего рода регуляризации избежать слишком хорошо!--13--> проблемы). Например, вы можете исправить ковариационную матрицу только диагональной или даже иметь ковариационные матрицы shared по всем Гаусса.
наконец, как только вы установили модель смеси, вы можете исследовать кластеры, вычисляя заднюю вероятность данных экземпляры, использующие каждый компонент смеси (как я показал в Примере 1D). GMM назначает каждый экземпляр кластеру в соответствии с этой вероятностью" членства".
вот более полный пример кластеризации данных с использованием Гауссовой модели смеси:
% load Fisher Iris dataset
load fisheriris
% project it down to 2 dimensions for the sake of visualization
[~,data] = pca(meas,'NumComponents',2);
mn = min(data); mx = max(data);
D = size(data,2); % data dimension
% inital kmeans step used to initialize EM
K = 3; % number of mixtures/clusters
cInd = kmeans(data, K, 'EmptyAction','singleton');
% fit a GMM model
gmm = fitgmdist(data, K, 'Options',statset('MaxIter',1000), ...
'CovType','full', 'SharedCov',false, 'Regularize',0.01, 'Start',cInd);
% means, covariances, and mixing-weights
mu = gmm.mu;
sigma = gmm.Sigma;
p = gmm.PComponents;
% cluster and posterior probablity of each instance
% note that: [~,clustIdx] = max(p,[],2)
[clustInd,~,p] = cluster(gmm, data);
tabulate(clustInd)
% plot data, clustering of the entire domain, and the GMM contours
clrLite = [1 0.6 0.6 ; 0.6 1 0.6 ; 0.6 0.6 1];
clrDark = [0.7 0 0 ; 0 0.7 0 ; 0 0 0.7];
[X,Y] = meshgrid(linspace(mn(1),mx(1),50), linspace(mn(2),mx(2),50));
C = cluster(gmm, [X(:) Y(:)]);
image(X(:), Y(:), reshape(C,size(X))), hold on
gscatter(data(:,1), data(:,2), species, clrDark)
h = ezcontour(@(x,y)pdf(gmm,[x y]), [mn(1) mx(1) mn(2) mx(2)]);
set(h, 'LineColor','k', 'LineStyle',':')
hold off, axis xy, colormap(clrLite)
title('2D data and fitted GMM'), xlabel('PC1'), ylabel('PC2')
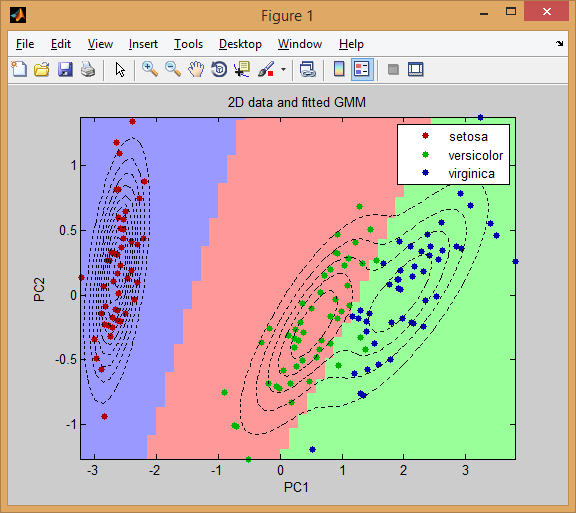
вы правы, есть то же самое понимание кластеризации с помощью K-Means или GMM. Но, как вы упомянули, Гауссовы смеси учитывают ковариации данных. Чтобы найти параметры максимального правдоподобия (или максимальную апостериорную карту) статистической модели GMM, необходимо использовать итерационный процесс алгоритм EM. Каждая итерация состоит из E-шага (ожидание) и M-шага (максимизация) и повторяется до сходимости. После конвергенции вы можете легко оценка вероятности принадлежности каждого вектора данных для каждой кластерной модели.
ковариация говорит вам, как данные меняются в пространстве, если распределение имеет большую ковариацию, это означает, что данные более распространены и наоборот. Когда у вас есть PDF-файл гауссова распределения (средние и ковариационные параметры), вы можете проверить уверенность в членстве тестовой точки в этом распределении.
однако GMM также страдает от слабости K-означает, что вы должны выбрать параметр K, который является количеством кластеров. Это требует хорошего понимания вашего многомодальность данных.
