Понимание составляющей деконволюции

Я пытаюсь понять scipy.signal.deconvolve.

С математической точки зрения свертка-это просто умножение в Фурье-пространстве, так что я ожидаю что для двух функций f и g:
Deconvolve(Convolve(f,g) , g) == f

в numpy / scipy это либо не так, либо я упускаю важный момент. Хотя есть некоторые вопросы, связанные с деконволюции так уже (как здесь и здесь) они не обратитесь к этому пункту, другие остаются неясными (этой) или без ответа (здесь). Есть также два вопроса о SignalProcessing SE (этой и этой), ответы на которые не полезны для понимания того, как функционируют деконволюции составляющей работы по.

вопрос такой:

  • как восстановить исходный сигнал f от запутанного сигнала, если вы знаете функцию свертки г.?
  • или другими словами: как этот псевдокод Deconvolve(Convolve(f,g) , g) == f перевести на numpy / scipy?

редактировать: обратите внимание, что этот вопрос не направлен на предотвращение числовых неточностей (хотя это также открытый вопрос) но при понимании того, как свертка/деконволюция работают вместе в scipy.

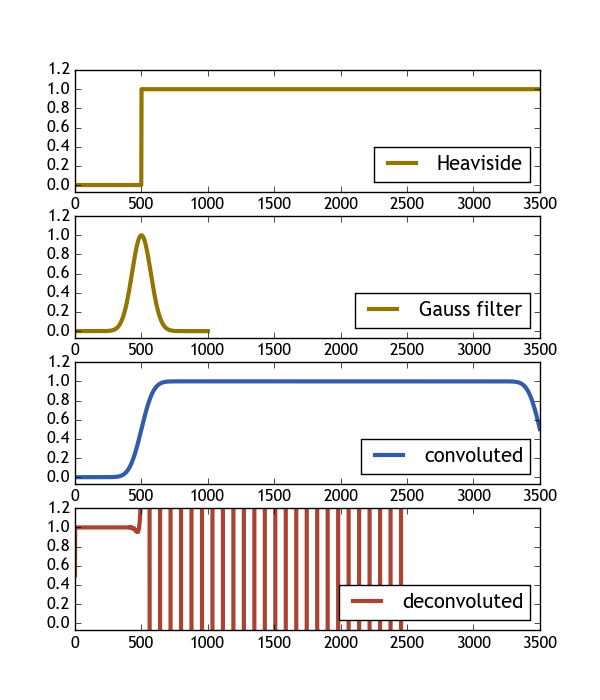
следующий код пытается сделать это с помощью функции Heaviside и гауссова фильтра. Как видно в результате деконволюции свертки не вся оригинальная функция Heaviside. Я был бы рад, если бы кто-то мог пролить свет на эту проблему.

import numpy as np
import scipy.signal
import matplotlib.pyplot as plt

# Define heaviside function
H = lambda x: 0.5 * (np.sign(x) + 1.)
#define gaussian
gauss = lambda x, sig: np.exp(-( x/float(sig))**2 )

X = np.linspace(-5, 30, num=3501)
X2 = np.linspace(-5,5, num=1001)

# convolute a heaviside with a gaussian
H_c = np.convolve( H(X),  gauss(X2, 1),  mode="same"  )
# deconvolute a the result
H_dc, er = scipy.signal.deconvolve(H_c, gauss(X2, 1) )


#### Plot #### 
fig , ax = plt.subplots(nrows=4, figsize=(6,7))
ax[0].plot( H(X),          color="#907700", label="Heaviside",    lw=3 ) 
ax[1].plot( gauss(X2, 1),  color="#907700", label="Gauss filter", lw=3 )
ax[2].plot( H_c/H_c.max(), color="#325cab", label="convoluted" ,  lw=3 ) 
ax[3].plot( H_dc,          color="#ab4232", label="deconvoluted", lw=3 ) 
for i in range(len(ax)):
    ax[i].set_xlim([0, len(X)])
    ax[i].set_ylim([-0.07, 1.2])
    ax[i].legend(loc=4)
plt.show()

enter image description here

редактировать: обратите внимание, что есть пример matlab, показывая, как свернуть / деконволюции прямоугольный сигнал с помощью

yc=conv(y,c,'full')./sum(c); 
ydc=deconv(yc,c).*sum(c);

в духе этого вопроса это также поможет если кто-то смог перевести этот пример на python.

10
deconvolution numpy python scipy signals

2 ответов

после некоторых проб и ошибок я выяснил, как интерпретировать результаты scipy.signal.deconvolve() и я публикую свои выводы в качестве ответа.

давайте начнем с рабочего примера кода

import numpy as np
import scipy.signal
import matplotlib.pyplot as plt

# let the signal be box-like
signal = np.repeat([0., 1., 0.], 100)
# and use a gaussian filter
# the filter should be shorter than the signal
# the filter should be such that it's much bigger then zero everywhere
gauss = np.exp(-( (np.linspace(0,50)-25.)/float(12))**2 )
print gauss.min()  # = 0.013 >> 0

# calculate the convolution (np.convolve and scipy.signal.convolve identical)
# the keywordargument mode="same" ensures that the convolution spans the same
#   shape as the input array.
#filtered = scipy.signal.convolve(signal, gauss, mode='same') 
filtered = np.convolve(signal, gauss, mode='same') 

deconv,  _ = scipy.signal.deconvolve( filtered, gauss )
#the deconvolution has n = len(signal) - len(gauss) + 1 points
n = len(signal)-len(gauss)+1
# so we need to expand it by 
s = (len(signal)-n)/2
#on both sides.
deconv_res = np.zeros(len(signal))
deconv_res[s:len(signal)-s-1] = deconv
deconv = deconv_res
# now deconv contains the deconvolution 
# expanded to the original shape (filled with zeros) 


#### Plot #### 
fig , ax = plt.subplots(nrows=4, figsize=(6,7))

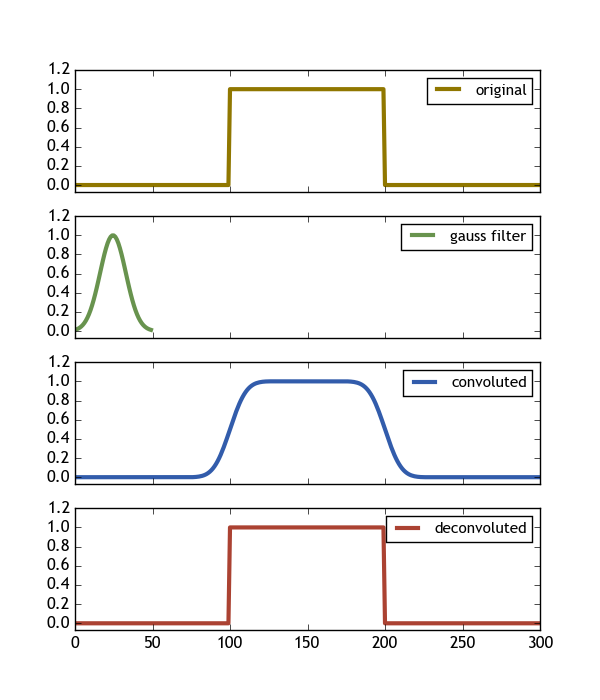
ax[0].plot(signal,            color="#907700", label="original",     lw=3 ) 
ax[1].plot(gauss,          color="#68934e", label="gauss filter", lw=3 )
# we need to divide by the sum of the filter window to get the convolution normalized to 1
ax[2].plot(filtered/np.sum(gauss), color="#325cab", label="convoluted" ,  lw=3 )
ax[3].plot(deconv,         color="#ab4232", label="deconvoluted", lw=3 ) 

for i in range(len(ax)):
    ax[i].set_xlim([0, len(signal)])
    ax[i].set_ylim([-0.07, 1.2])
    ax[i].legend(loc=1, fontsize=11)
    if i != len(ax)-1 :
        ax[i].set_xticklabels([])

plt.savefig(__file__ + ".png")
plt.show()

этот код создает следующее изображение, показывая именно то, что мы хотим (Deconvolve(Convolve(signal,gauss) , gauss) == signal)

enter image description here

некоторые важные выводы:

  • фильтр должен быть короче, чем сигнал
  • фильтр должен быть гораздо больше нуля везде (здесь > 0.013 достаточно хорошо)
  • использование ключевого слова argument mode = 'same' к свертке обеспечивает что она живет на такой же форме массива как сигнал.
  • деконволюция имеет n = len(signal) - len(gauss) + 1 очков. Поэтому, чтобы он также находился на той же исходной форме массива, нам нужно расширить его на s = (len(signal)-n)/2 С обеих сторон.

конечно, дальнейшие выводы, комментарии и предложения по этому вопросу по-прежнему приветствуются.

7

как написано в комментариях, я не могу помочь с примером, который вы опубликовали изначально. Как отметил @Stelios, деконволюция может не сработать из-за численных проблем.

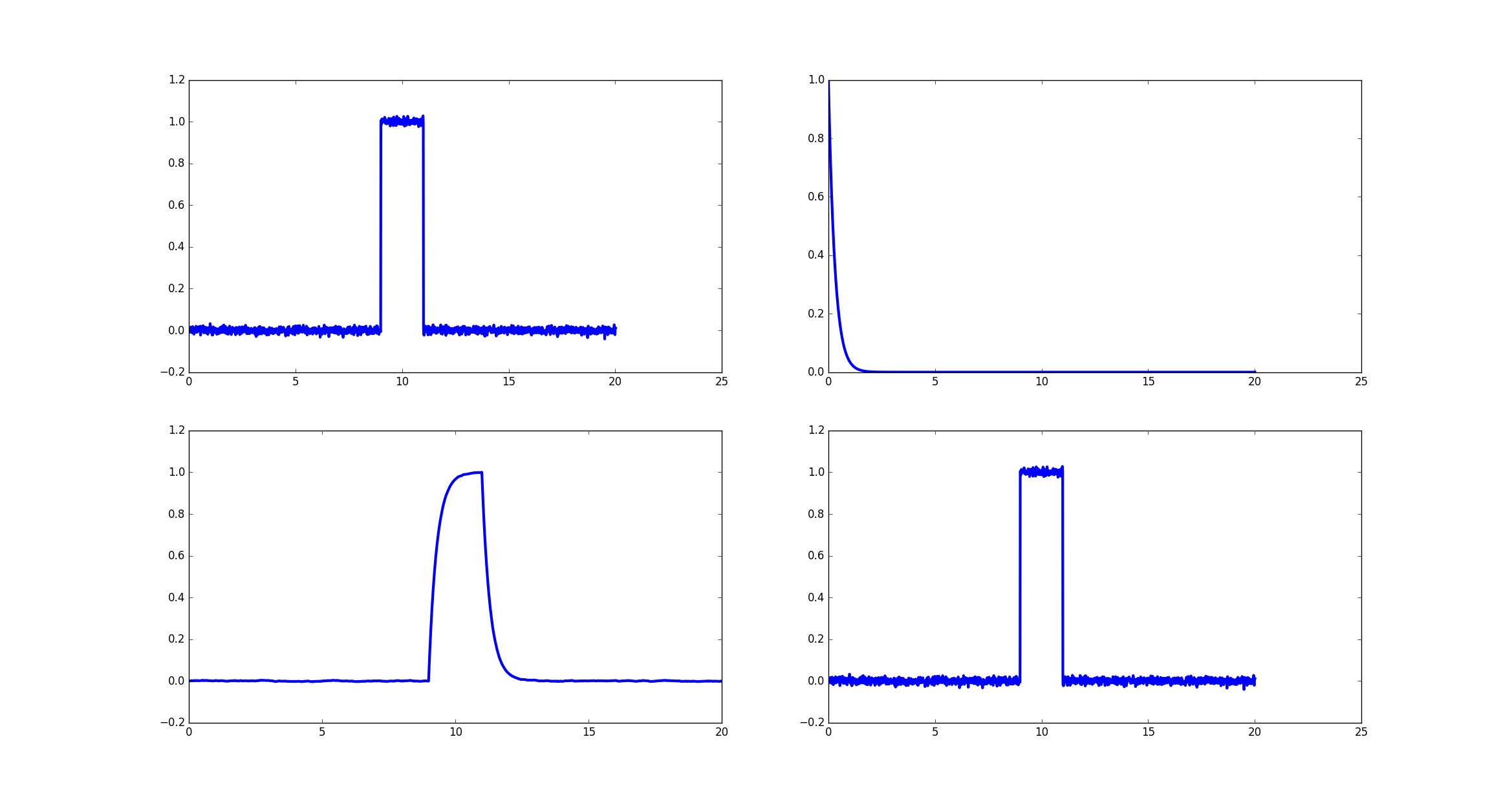
Я могу, однако, воспроизвести пример, который вы опубликовали в своем редактировании:

enter image description here

это код, который является прямым переводом из исходного кода matlab:

import numpy as np
import scipy.signal
import matplotlib.pyplot as plt

x = np.arange(0., 20.01, 0.01)
y = np.zeros(len(x))
y[900:1100] = 1.
y += 0.01 * np.random.randn(len(y))
c = np.exp(-(np.arange(len(y))) / 30.)

yc = scipy.signal.convolve(y, c, mode='full') / c.sum()
ydc, remainder = scipy.signal.deconvolve(yc, c)
ydc *= c.sum()

fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(4, 4))
ax[0][0].plot(x, y, label="original y", lw=3)
ax[0][1].plot(x, c, label="c", lw=3)
ax[1][0].plot(x[0:2000], yc[0:2000], label="yc", lw=3)
ax[1][1].plot(x, ydc, label="recovered y", lw=3)

plt.show()
4