Попытка понять математику за перспективной матрицей в WebGL

давайте посмотрим, смогу ли я объяснить это, или, может быть, после прочтения этого вы можете придумать лучший способ объяснить это.

первое, что нужно понять, это то, что WebGL требует координат clipspace. Они идут -1 +1 в x, y и z. Таким образом, перспективная матрица в основном предназначена для размещения пространства внутри усеченного и преобразовать его в clipspace.

если вы посмотрите на эту диаграмму

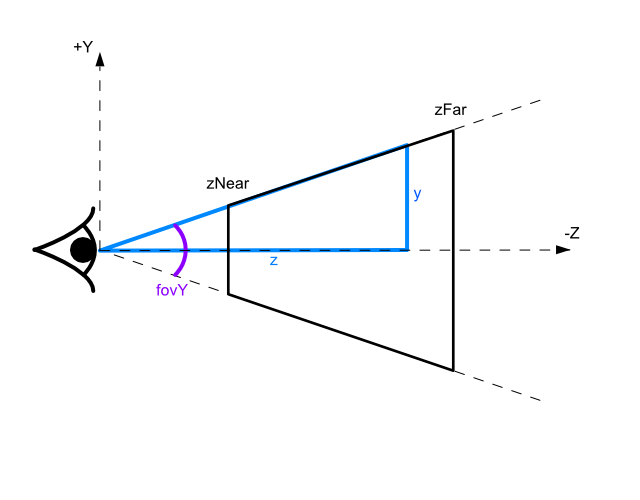
мы знаем, что тангенс = напротив(y) над смежным (z), поэтому, если мы знаем z, мы можем вычислить y, который будет сидеть на краю разочарования для данного fovY.

tan(fovY / 2) = y / -z

умножьте обе стороны на-z

y = tan(fovY / 2) * -z

если мы определяем

f = 1 / tan(fovY / 2)

мы

y = -z / f

обратите внимание, что мы не сделали преобразование из cameraspace в clipspace. Все, что мы сделали, это вычислить y на краю поля зрения для данного z в cameraspace. На краю поля зрения края clipspace. Поскольку clipspace это просто +1 до -1, мы можем просто разделить cameraspace г по -z / f чтобы получить clipspace.

это имеет смысл? Посмотрите на диаграмму еще раз. Предположим, что синий z был -5 и для некоторого заданного поля зрения до +2.34. Нам нужно преобразовать +2.34 к +1 clipspace. Общая версия этого -

clipY = cameraY * f / -z

глядя на 'makePerspective'

function makePerspective(fieldOfViewInRadians, aspect, near, far) {
  var f = Math.tan(Math.PI * 0.5 - 0.5 * fieldOfViewInRadians);
  var rangeInv = 1.0 / (near - far);

  return [
    f / aspect, 0, 0, 0,
    0, f, 0, 0,
    0, 0, (near + far) * rangeInv, -1,
    0, 0, near * far * rangeInv * 2, 0
  ];
};

мы видим, что f в этом случае

tan(Math.PI * 0.5 - 0.5 * fovY)

что на самом деле то же самое, что

1 / tan(fovY / 2)

почему так написано? Я предполагаю, потому что если бы у вас был первый стиль, а tan вышел на 0, вы бы разделили на 0, ваша программа рухнула бы, если бы вы сделали это таким образом, нет никакого деления, поэтому нет шансов на деление на ноль.

видя, что -1 находится в matrix[11] spot означает, когда мы все сделал

matrix[5]  = tan(Math.PI * 0.5 - 0.5 * fovY)
matrix[11] = -1

clipY = cameraY * matrix[5] / cameraZ * matrix[11]

For clipX мы в основном делаем тот же расчет только увеличить пропорции.

matrix[0]  = tan(Math.PI * 0.5 - 0.5 * fovY) / aspect
matrix[11] = -1

clipX = cameraX * matrix[0] / cameraZ * matrix[11]

наконец, мы должны преобразовать cameraZ в-zNear - zFar диапазон в clipZ в -1 + 1 диапазон.

стандартная перспективная матрица делает это с помощью as взаимные функции чтобы значения z закрывали камеру, получите больше разрешения, чем значения z вдали от камеры. Эта формула is

clipZ = something / cameraZ + constant

давайте s на something и c для постоянного.

clipZ = s / cameraZ + c;

и решить для s и c. В нашем случае мы знаем!--58-->

s / -zNear + c = -1
s / -zFar  + c =  1

Итак, переместите " c " на другую сторону

s / -zNear = -1 - c
s / -zFar  =  1 - c

умножить на-zXXX

s = (-1 - c) * -zNear
s = ( 1 - c) * -zFar

эти 2 вещи равны друг другу так

(-1 - c) * -zNear = (1 - c) * -zFar

расширить количество

(-zNear * -1) - (c * -zNear) = (1 * -zFar) - (c * -zFar)

упростить

zNear + c * zNear = -zFar + c * zFar

переместить zNear справа

c * zNear = -zFar + c * zFar - zNear

движение c * zFar налево

c * zNear - c * zFar = -zFar - zNear

упростить

c * (zNear - zFar) = -(zFar + zNear)

разделить на (zNear - zFar)

c = -(zFar + zNear) / (zNear - zFar)

решить s

s = (1 - -((zFar + zNear) / (zNear - zFar))) * -zFar

упростить

s = (1 + ((zFar + zNear) / (zNear - zFar))) * -zFar

изменить 1 до (zNear - zFar)

s = ((zNear - zFar + zFar + zNear) / (zNear - zFar)) * -zFar

упростить

s = ((2 * zNear) / (zNear - zFar)) * -zFar

упростите еще немного

s = (2 * zNear * zFar) / (zNear - zFar)

dang я хочу, чтобы stackexchange поддерживал математику, как их математический сайт делает : (

Итак, вернемся к началу. Наш форумла был

s / cameraZ + c

и мы знаем!--41--> и c сейчас.

clipZ = (2 * zNear * zFar) / (zNear - zFar) / -cameraZ -
        (zFar + zNear) / (zNear - zFar)

давайте переместим-z снаружи

clipZ = ((2 * zNear * zFar) / zNear - ZFar) +
         (zFar + zNear) / (zNear - zFar) * cameraZ) / -cameraZ

мы можем изменить / (zNear - zFar) to * 1 / (zNear - zFar) так

rangeInv = 1 / (zNear - zFar)
clipZ = ((2 * zNear * zFar) * rangeInv) +
         (zFar + zNear) * rangeInv * cameraZ) / -cameraZ

оглядываясь на makeFrustum мы видим, что это в конечном итоге делает

clipZ = (matrix[10] * cameraZ + matrix[14]) / (cameraZ * matrix[11])

глядя на Формулу выше, которая подходит

rangeInv = 1 / (zNear - zFar)
matrix[10] = (zFar + zNear) * rangeInv
matrix[14] = 2 * zNear * zFar * rangeInv
matrix[11] = -1
clipZ = (matrix[10] * cameraZ + matrix[14]) / (cameraZ * matrix[11])

я надеюсь, что имело смысл. Примечание: большая часть этого-просто мое переписывание в этой статье.