Построение БПФ на Октаве

Я знаю, что FFT изменяет функцию во временной области на ту, которая показана в частотной области.

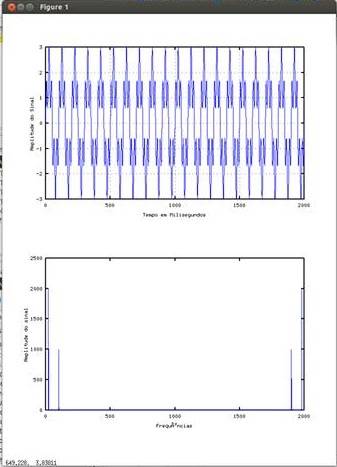
однако, когда я пытаюсь построить указанный график в частотной области, я могу заставить его работать правильно, используя время как ось X, когда это, очевидно, должно было быть не это, а частота.

кроме того, я могу получить амплитуды, соответствующие амплитудам исходного сигнала, только разделив ось y на определенное целое число. Почему так?

вот мой код

t=0:0.001:2

x=2*sin(20*pi*t) + sin(100*pi*t)
subplot(2,1,1)
plot(1000*t,x)
grid
xlabel("Time in milliseconds")
ylabel("Signal amplitude")

subplot(2,1,2)
y=fft(x)
plot(1000*t,abs(y))
xlabel("Frequency")
ylabel("Signal amplitude")

и графики.

enter image description here

пожалуйста, помогите =(

10
fft octave plot signal-processing

2 ответов

отношение частоты (масштабирование по оси x)

частота каждого значения, производимого БПФ, линейно связана с индексом выходного значения через:

f(i) = (i-1)*sampling_frequency/N

где N-количество точек БПФ (т. е. N=length(y)). В твоем случае, N=2001.

можно вычесть частоту дискретизации из вашего определения t как 1/T, где T-интервал времени выборки (T=0.001 в вашем случае). Так частота дискретизации 1000Гц.

обратите внимание, что так как значение t(i) также линейно связан с индексом i, через

t(i) = (i-1)*0.001

можно (хотя и не обязательно советовать, так как это просто затенит ваш код) определить f = 1000*t*sampling_frequency/N. Обратите внимание, что вы пропустили sampling_frequency/N термин, который соответственно привел к тонам, показанным на неправильной частоте (из определения x должны быть пики на 10Hz и 50Hz, и соответствуя псевдонимы на 990Hz и 950Hz).

отношение амплитуды (масштабирование по оси y)

обратите внимание, что наблюдаемая связь является только приблизительной, поэтому следующее не является математическим доказательством, а просто интуитивным способом визуализации связи между амплитудами тона во временной области и пиковыми значениями в частотной области.

упрощение проблемы до одного тона:

x = A*sin(2*pi*f*t)

приблизительная амплитуда соответствуя пика смогла быть производное с использованием Поншеваль это!--42-->:

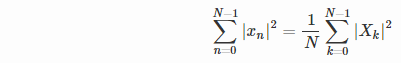
enter image description here

во временной области (левая часть уравнения), выражение приблизительно равна 0.5*N*(A^2).

в частотной области (в правой части уравнения), делая следующие предположения:

  • спектральные эффекты утечки ничтожны
  • спектральное содержание тона содержится только в 2 бункерах (на частоте f и соответствующая псевдонимная частота sampling_frequency-f) учет суммирования (все остальные бункеры ~0). Обратите внимание, что это обычно выполняется, только если частота тона является точной (или почти точной) кратной sampling_frequency/N.

выражение на правой стороне приблизительно равно 2*(1/N)*abs(X(k))^2 для некоторого значения k соответствует пику на частоте f.

сложение двух вместе дает abs(X(k)) ~ 0.5*A*N. Другими словами, амплитуда выходного сигнала показывает коэффициент масштабирования 0.5*N (или примерно 1000 в вашем случае) относительно амплитуды временной области, как вы заметили.

идея по-прежнему применяется с более чем одним тоном (хотя незначительное предположение о спектральной утечке в конечном итоге ломается).

13

в других ответах было предложено, что в этом примере есть частотные характеристики при 950Hz и 990Hz. Это недоразумение о том, как код FFT использует индексы. Эти" высокочастотные " Шипы на самом деле-50Hz и-10Hz.

частотная область простирается от -N / 2 * sampling_frequency/N до + N / 2*sampling_frequency / N. Но по историческим причинам соглашение заключается в том, что первые N/2 части информации являются положительными частотами, средняя точка нулевая частота и последние N/2 единиц информации являются отрицательными частотами в обратном порядке. Для спектра мощности нет необходимости показывать больше, чем первые 1+N/2 части информации.

Это соглашение чрезвычайно запутанно, так как мне пришлось разгадать его из Press et al. Численные рецепты и кодирование быстрого преобразования Хартли вручную, много лет назад, когда я впервые использовал БПФ, предшествуя бета-тестовому изданию Matlab 1.0, которое Клив Молер передал некоторым повезло докторантов :-)

3