Построение данных из svm fit-гиперплоскости

вы писали:

я СВМ найти гиперплоскость регрессии наилучшего вписывания

но согласно:

Call:
svm(formula = q ~ ., data = data, kernel = "linear")

Parameters:
SVM-Type:  C-classification

вы делаете классификация.

Итак, прежде всего решите, что вам нужно: классифицировать или соответствовать регрессии, от ?svm, мы видим:

type: ‘svm’ can be used as a classification machine, as a
      regression machine, or for novelty detection.  Depending of
      whether ‘y’ is a factor or not, the default setting for
      ‘type’ is ‘C-classification’ or ‘eps-regression’,
      respectively, but may be overwritten by setting an explicit
      value.

как я считаю, вы не изменили параметр type значение по умолчанию, вы, вероятно, решением classification, так что я буду покажите, как визуализировать это для классификации.

предположим есть 2 классов, генерировать некоторые данные:

> require(e1071) # for svm()                                                                                                                                                          
> require(rgl) # for 3d graphics.                                                                                                                                                                                    
> set.seed(12345)                                                                                                                                                                     
> seed <- .Random.seed                                                                                                                                                                
> t <- data.frame(x=runif(100), y=runif(100), z=runif(100), cl=NA)
> t$cl <- 2 * t$x + 3 * t$y - 5 * t$z                                                                                                                                                 
> t$cl <- as.factor(ifelse(t$cl>0,1,-1))
> t[1:4,]
           x         y         z cl
 1 0.7209039 0.2944654 0.5885923 -1
 2 0.8757732 0.6172537 0.8925918 -1
 3 0.7609823 0.9742741 0.1237949  1
 4 0.8861246 0.6182120 0.5133090  1

так как вы хотите kernel='linear' граница должна быть w1*x + w2*y + w3*z - w0 - гиперплоскость. Наша задача делится на 2 подзадачи: 1) оценить уравнение этой граничной плоскости 2) нарисовать эту плоскость.

1) оценка уравнения граничной плоскости

сначала запускаем svm():

> svm_model <- svm(cl~x+y+z, t, type='C-classification', kernel='linear',scale=FALSE)

я написал здесь явно type=C-classification просто для акцента мы хотим сделать классификация. scale=FALSE означает, что мы хотим svm() для запуска непосредственно с предоставленными данными без масштабирования данных (как это делается по умолчанию). Я сделал это для будущих оценок, которые станут проще.

к сожалению, svm_model не хранит уравнение граничной плоскости (или просто нормальный вектор), поэтому мы должны его оценить. От svm-алгоритм мы знаем, что мы можем оценить такие веса со следующими формула:

w <- t(svm_model$coefs) %*% svm_model$SV

отрицательный перехват хранится в svm_model, и через svm_model$rho.

2) чертеж самолета.

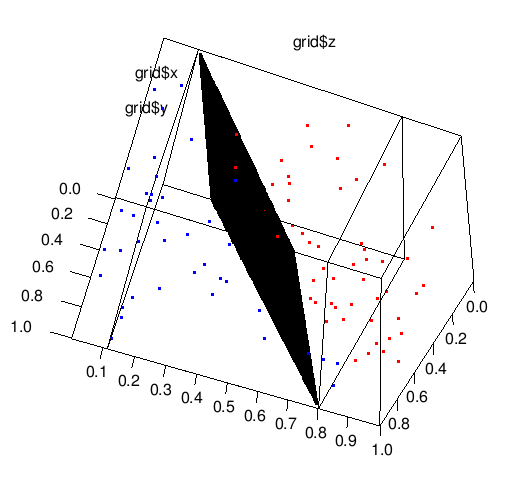
я не нашел никакой полезной функции plane3d, Итак, снова мы должны сделать некоторую удобную работу. Мы просто берем сетку пар (x,y) и оцените соответствующее значение z границы плоскости.

detalization <- 100                                                                                                                                                                 
grid <- expand.grid(seq(from=min(t$x),to=max(t$x),length.out=detalization),                                                                                                         
                    seq(from=min(t$y),to=max(t$y),length.out=detalization))                                                                                                         
z <- (svm_model$rho- w[1,1]*grid[,1] - w[1,2]*grid[,2]) / w[1,3]

plot3d(grid[,1],grid[,2],z)  # this will draw plane.
# adding of points to the graphics.
points3d(t$x[which(t$cl==-1)], t$y[which(t$cl==-1)], t$z[which(t$cl==-1)], col='red')
points3d(t$x[which(t$cl==1)], t$y[which(t$cl==1)], t$z[which(t$cl==1)], col='blue')

С rgl пакета, вы можете повернуть это изображение и наслаждаться ею :)