Повторные числа MATLAB на основе вектора длин
есть ли векторизованный способ сделать следующее? (показано на примере):
input_lengths = [ 1 1 1 4 3 2 1 ]
result = [ 1 2 3 4 4 4 4 5 5 5 6 6 7 ]
я разнес input_lengths, поэтому легко понять, как получается результат
результирующий вектор имеет длину: sum(lengths). В настоящее время я вычисляю result использовать следующий цикл:
result = ones(1, sum(input_lengths ));
counter = 1;
for i = 1:length(input_lengths)
start_index = counter;
end_index = counter + input_lengths (i) - 1;
result(start_index:end_index) = i;
counter = end_index + 1;
end
EDIT:
Я также могу сделать это с помощью arrayfun (хотя это не совсем векторизованная функция)
cell_result = arrayfun(@(x) repmat(x, 1, input_lengths(x)), 1:length(input_lengths), 'UniformOutput', false);
cell_result : {[1], [2], [3], [4 4 4 4], [5 5 5], [6 6], [7]}
result = [cell_result{:}];
result : [ 1 2 3 4 4 4 4 5 5 5 6 6 7 ]
6 ответов
result = zeros(1,sum(input_lengths));
result(cumsum([1 input_lengths(1:end-1)])) = 1;
result = cumsum(result);
Это должно быть довольно быстро. И использование памяти минимально возможное.
оптимизированная версия вышеуказанного кода, из-за Bentoy13 (см. Его очень детальный бенчмаркинг):
result = zeros(1,sum(input_lengths));
result(1) = 1;
result(1+cumsum(input_lengths(1:end-1))) = 1;
result = cumsum(result);
полностью векторизованная версия:
selector=bsxfun(@le,[1:max(input_lengths)]',input_lengths);
V=repmat([1:size(selector,2)],size(selector,1),1);
result=V(selector);
недостатком является использование памяти O (numel(input_lengths) * max(input_lengths))
тест всех решений
после предыдущего ориентира, Я группирую все решения, приведенные здесь в скрипте, и запускаю его несколько часов для бенчмарка. Я сделал это, потому что я думаю, что хорошо посмотреть, какова производительность каждого предлагаемого решения с входной длиной в качестве параметра - мое намерение не здесь, чтобы записать качество предыдущего, что дает дополнительную информацию о влиянии JIT. Более того, и каждый участник, кажется, согласитесь с этим, во всех ответах была проделана неплохая работа, поэтому этот отличный пост заслуживает вывода.
Я не буду размещать код скрипта здесь, это довольно долго и очень неинтересно. Процедура теста состоит в том, чтобы выполнить каждое решение для набора разной длины входных векторов: 10, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000, 20000, 50000, 100000, 200000, 500000, 1000000. Для каждой входной длины я сгенерировал случайный входной вектор на основе закона Пуассона с параметр 0.8 (чтобы избежать больших значений):
input_lengths = round(-log(1-rand(1,ILen(i)))/poisson_alpha)+1;
наконец, я усредняю время вычисления более 100 запусков на входную длину.
я запустил скрипт на своем ноутбуке (core I7) с Matlab R2013b; JIT активирован.
и вот построенные результаты (извините, цветные линии) в масштабе журнала (ось x: входная длина; ось y: время вычисления в секундах):
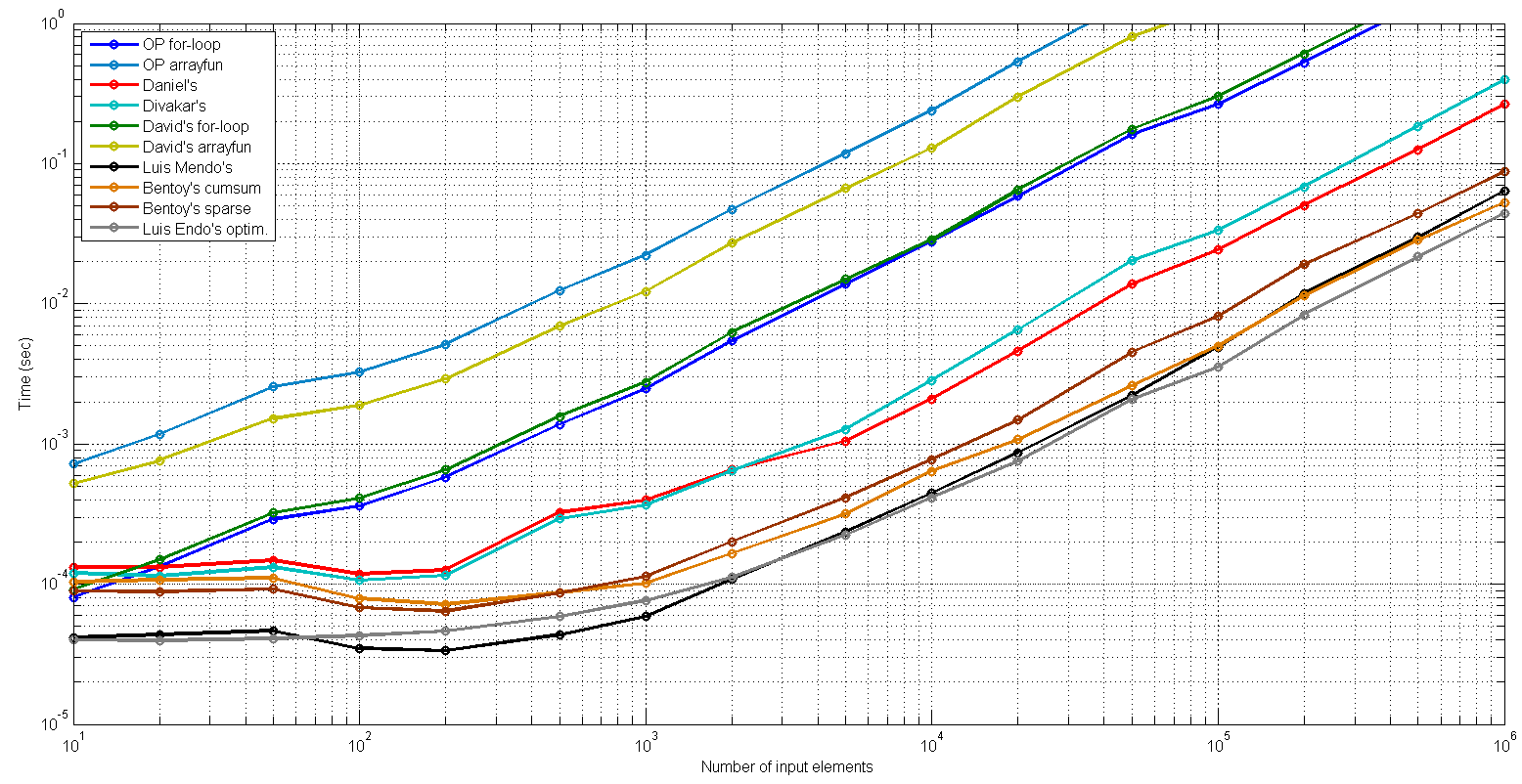
Итак, Луис Мендо-явный победитель, поздравляю!
для тех, кто хочет получить численные результаты и / или хочет их пересчитать, вот они (разрежьте таблицу на 2 части и приблизьте к 3 цифрам для лучшего отображения):
N 10 20 50 100 200 500 1e+03 2e+03
-------------------------------------------------------------------------------------------------------------
OP's for-loop 8.02e-05 0.000133 0.00029 0.00036 0.000581 0.00137 0.00248 0.00542
OP's arrayfun 0.00072 0.00117 0.00255 0.00326 0.00514 0.0124 0.0222 0.047
Daniel 0.000132 0.000132 0.000148 0.000118 0.000126 0.000325 0.000397 0.000651
Divakar 0.00012 0.000114 0.000132 0.000106 0.000115 0.000292 0.000367 0.000641
David's for-loop 9.15e-05 0.000149 0.000322 0.00041 0.000654 0.00157 0.00275 0.00622
David's arrayfun 0.00052 0.000761 0.00152 0.00188 0.0029 0.00689 0.0122 0.0272
Luis Mendo 4.15e-05 4.37e-05 4.66e-05 3.49e-05 3.36e-05 4.37e-05 5.87e-05 0.000108
Bentoy13's cumsum 0.000104 0.000107 0.000111 7.9e-05 7.19e-05 8.69e-05 0.000102 0.000165
Bentoy13's sparse 8.9e-05 8.82e-05 9.23e-05 6.78e-05 6.44e-05 8.61e-05 0.000114 0.0002
Luis Mendo's optim. 3.99e-05 3.96e-05 4.08e-05 4.3e-05 4.61e-05 5.86e-05 7.66e-05 0.000111
N 5e+03 1e+04 2e+04 5e+04 1e+05 2e+05 5e+05 1e+06
-------------------------------------------------------------------------------------------------------------
OP's for-loop 0.0138 0.0278 0.0588 0.16 0.264 0.525 1.35 2.73
OP's arrayfun 0.118 0.239 0.533 1.46 2.42 4.83 12.2 24.8
Daniel 0.00105 0.0021 0.00461 0.0138 0.0242 0.0504 0.126 0.264
Divakar 0.00127 0.00284 0.00655 0.0203 0.0335 0.0684 0.185 0.396
David's for-loop 0.015 0.0286 0.065 0.175 0.3 0.605 1.56 3.16
David's arrayfun 0.0668 0.129 0.299 0.803 1.33 2.64 6.76 13.6
Luis Mendo 0.000236 0.000446 0.000863 0.00221 0.0049 0.0118 0.0299 0.0637
Bentoy13's cumsum 0.000318 0.000638 0.00107 0.00261 0.00498 0.0114 0.0283 0.0526
Bentoy13's sparse 0.000414 0.000774 0.00148 0.00451 0.00814 0.0191 0.0441 0.0877
Luis Mendo's optim. 0.000224 0.000413 0.000754 0.00207 0.00353 0.00832 0.0216 0.0441
Ок, я добавил еще одно решение в список ... Я не мог помешать себе оптимизировать лучшее на данный момент решение Луиса Мендо. Это не заслуга, это просто вариант Луиса Мендо, я объясню позже.
ясно, что решения с использованием arrayfun очень трудоемкий. Решения, использующие явный цикл for, быстрее, но все же медленнее по сравнению с другими решениями. Так что да, векторизация по-прежнему является основным вариантом оптимизации сценария Matlab.
поскольку я видел большую дисперсию по вычислительным временам самых быстрых решений, особенно с входными длинами между 100 и 10000, я решил проверить более точно. Поэтому я поставил самый медленный (извините) и повторил тест над 6 другими решениями, которые работают намного быстрее. Этот второй тест над этим сокращенным списком решений идентичен, за исключением того, что у меня в среднем более 1000 запусков.
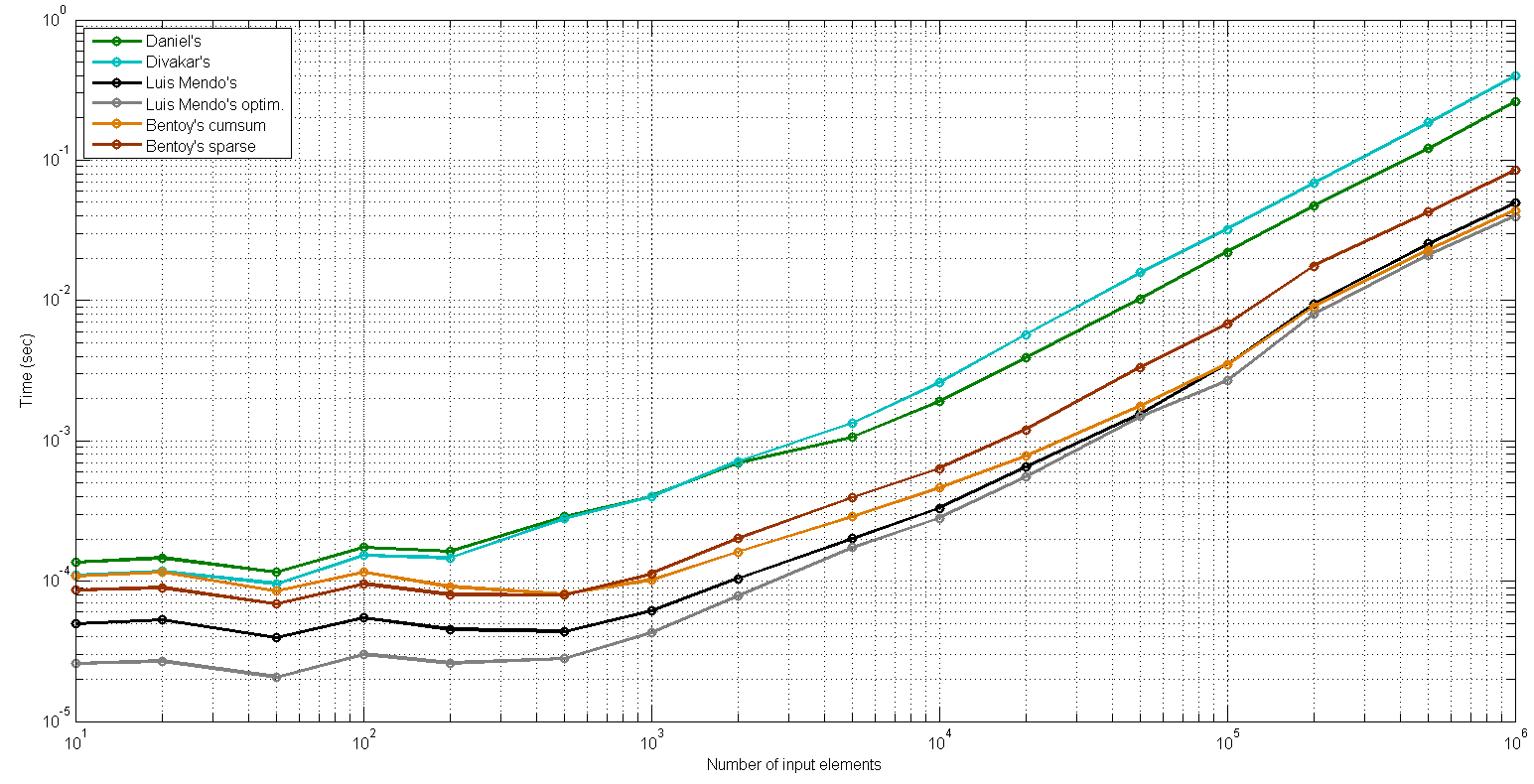
(здесь нет таблицы, если вы действительно не хотите, это те же числа, что и раньше)
как было отмечено, решение Даниила немного быстрее, чем решение Дивакара, потому что кажется, что использование bsxfun С @times медленнее, чем с помощью repmat. Тем не менее, они в 10 раз быстрее, чем решения для цикла: ясно, векторизация в Matlab-это хорошо.
решения Bentoy13 и Luis Mendo очень близки; первый использует больше инструкций, но второй использует дополнительное распределение при объединении 1 в cumsum(input_lengths(1:end-1)). И именно поэтому мы видим, что решение Bentoy13 имеет тенденцию быть немного быстрее с большими входными длинами (выше 5.10^5), потому что нет дополнительного выделения. Из этого рассмотрения я сделал оптимизированное решение, где нет дополнительного выделения; вот код (Luis Мендо может поставить это в своем ответе, если захочет:)):
result = zeros(1,sum(input_lengths));
result(1) = 1;
result(1+cumsum(input_lengths(1:end-1))) = 1;
result = cumsum(result);
любой комментарий для улучшения приветствуется.
больше комментарий, чем что-либо, но я сделал несколько тестов. Я попробовал for петли, и arrayfun, и я проверил свой for петли и arrayfun версия. Ваш for петля была самой быстрой. Я думаю, это потому, что это просто и позволяет компиляции JIT делать максимальную оптимизацию. Я использую Matlab, Октава может быть другой.
и сроки:
Solution: With JIT Without JIT
Sam for 0.74 1.22
Sam arrayfun 2.85 2.85
My for 0.62 2.57
My arrayfun 1.27 3.81
Divakar 0.26 0.28
Bentoy 0.07 0.06
Daniel 0.15 0.16
Luis Mendo 0.07 0.06
таким образом, код Бентоя очень быстрый, а код Луиса Мендо почти такая же скорость. И я полагаюсь на Джит слишком много!
и код для моих попыток
clc,clear
input_lengths = randi(20,[1 10000]);
% My for loop
tic()
C=cumsum(input_lengths);
D=diff(C);
results=zeros(1,C(end));
results(1,1:C(1))=1;
for i=2:length(input_lengths)
results(1,C(i-1)+1:C(i))=i*ones(1,D(i-1));
end
toc()
tic()
A=arrayfun(@(i) i*ones(1,input_lengths(i)),1:length(input_lengths),'UniformOutput',false);
R=[A{:}];
toc()
Это небольшой вариант @Daniel's ответ. Суть этого решения основана на этом решении. Теперь этот избегает repmat, таким образом, это немного более "оцифрованной" может. Вот код -
selector=bsxfun(@le,[1:max(input_lengths)]',input_lengths); %//'
V = bsxfun(@times,selector,1:numel(input_lengths));
result = V(V~=0)
для всех отчаявшихся шутка поиск людей
result = nonzeros(bsxfun(@times,bsxfun(@le,[1:max(input_lengths)]',input_lengths),1:numel(input_lengths)))
Я ищу элегантное решение, и я думаю Дэвид - хорошее начало. Я имею в виду, что можно генерировать индексы, где добавить один из предыдущего элемента.
для этого, если мы вычисляем cumsum входного вектора, мы получим:
cumsum(input_lengths)
ans = 1 2 3 7 10 12 13
это индексы концов последовательностей одинаковых чисел. Это не то, что мы хотим, поэтому мы переворачиваем вектор дважды, чтобы получить начало:
fliplr(sum(input_lengths)+1-cumsum(fliplr(input_lengths)))
ans = 1 2 3 4 8 11 13
вот в чем фокус. Вы переворачиваете вектор, кумсум его, чтобы получить концы перевернутого вектора, а затем переворачиваете назад; но вы должны вычесть вектор из общей длины выходного вектора (+1, потому что индекс начинается с 1), потому что кумсум применяется к перевернутому вектору.
как только вы это сделаете, это очень просто, вам просто нужно поставить 1 на вычисленные индексы и 0 в другом месте, и cumsum it:
idx_begs = fliplr(sum(input_lengths)+1-cumsum(fliplr(input_lengths)));
result = zeros(1,sum(input_lengths));
result(idx_begs) = 1;
result = cumsum(result);
редактировать
во-первых, пожалуйста, посмотрите на Луис Решение мендо, он очень близок к моему, но проще и немного быстрее (я не буду редактировать мой даже очень близко). Я думаю, что на сегодняшний день это самое быстрое решение из всех.
во-вторых, глядя на другие решения, я составил еще один однострочный, немного отличающийся от моего первоначального решения и от другой-вкладыша. Хорошо, это будет не очень читабельно, поэтому сделайте вдох:
result = cumsum( full(sparse(cumsum([1,input_lengths(1:end-1)]), ...
ones(1,length(input_lengths)), 1, sum(input_lengths),1)) );
Я разрезал его на две линии. Хорошо, теперь давайте объясним он.
аналогичная часть заключается в построении массива индексов, где необходимо увеличить значение текущего элемента. Для этого я использую решение Луиса Мендо. Чтобы построить в одной строке вектор решения, я использую здесь тот факт, что это на самом деле разреженное представление двоичного вектора, которое мы будем суммировать в самом конце. Этот разреженный вектор строится с использованием нашего вычисленного вектора индекса как X позиций, вектора 1 как y позиций и 1 Как значение для размещения в этих местах. Ля четвертый аргумент дается для точного общего размера вектора (важно, если последний элемент input_lengths не 1). Затем мы получаем полное представление этого разреженного вектора (иначе результат будет разреженным вектором без пустого элемента), и мы можем cumsum.
нет никакого использования этого решения, кроме как дать другое решение этой проблемы. Тест может показать, что он медленнее, чем мое исходное решение, из-за более тяжелой нагрузки на память.
