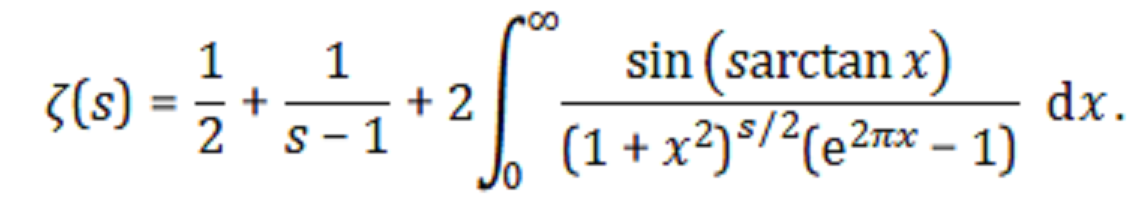Преобразование double в BigDecimal в Java
я написал Java-программу, которая вычисляет значения Дзета-функция Римана. Внутри программы я сделал библиотеку для вычисления необходимых сложных функций, таких как atan, cos и т. д. Все внутри обеих программ доступно через double и BigDecimal типы данных. Это создает серьезные проблемы при оценке больших значений для дзета-функции.
численное приближение для дзета-функции ссылки
прямая оценка этого приближения при высоких значениях создает проблемы, когда s имеет большую сложную форму, такую как s = (230+30i). Я очень благодарен за информацию об этом здесь. Оценка S2.minus(S1) создает ошибки, потому что я написал что-то неправильно в adaptiveQuad метод.
например, Zeta(2+3i) через эту программу генерирует
Calculation of the Riemann Zeta Function in the form Zeta(s) = a + ib.
Enter the value of [a] inside the Riemann Zeta Function: 2
Enter the value of [b] inside the Riemann Zeta Function: 3
The value for Zeta(s) is 7.980219851133409E-1 - 1.137443081631288E-1*i
Total time taken is 0.469 seconds.
что правильно.
Zeta(100+0i) создает
Calculation of the Riemann Zeta Function in the form Zeta(s) = a + ib.
Enter the value of [a] inside the Riemann Zeta Function: 100
Enter the value of [b] inside the Riemann Zeta Function: 0
The value for Zeta(s) is 1.000000000153236E0
Total time taken is 0.672 seconds.
что также правильно по сравнению с Вольфрам. Проблема связана с чем-то внутри метода с надписью adaptiveQuad.
Zeta(230+30i) создает
Calculation of the Riemann Zeta Function in the form Zeta(s) = a + ib.
Enter the value of [a] inside the Riemann Zeta Function: 230
Enter the value of [b] inside the Riemann Zeta Function: 30
The value for Zeta(s) is 0.999999999999093108519845391615339162047254997503854254342793916541606842461539820124897870147977114468145672577664412128509813042591501204781683860384769321084473925620572315416715721728082468412672467499199310913504362891199180150973087384370909918493750428733837552915328069343498987460727711606978118652477860450744628906250 - 38.005428584222228490409289204403133867487950535704812764806874887805043029499897666636162309572126423385487374863788363786029170239477119910868455777891701471328505006916099918492113970510619110472506796418206225648616641319533972054228283869713393805956289770456519729094756021581247296126093715429306030273437500E-15*i
Total time taken is 1.746 seconds.
воображаемая часть немного отличается по сравнению с Вольфрам.
алгоритм оценки интеграла известен как Адаптивная Квадратура и double Java реализация нашел здесь. Адаптивный метод quad применяется следующим образом
// adaptive quadrature
public static double adaptive(double a, double b) {
double h = b - a;
double c = (a + b) / 2.0;
double d = (a + c) / 2.0;
double e = (b + c) / 2.0;
double Q1 = h/6 * (f(a) + 4*f(c) + f(b));
double Q2 = h/12 * (f(a) + 4*f(d) + 2*f(c) + 4*f(e) + f(b));
if (Math.abs(Q2 - Q1) <= EPSILON)
return Q2 + (Q2 - Q1) / 15;
else
return adaptive(a, c) + adaptive(c, b);
}
вот моя четвертая попытка написать программу
/**************************************************************************
**
** Abel-Plana Formula for the Zeta Function
**
**************************************************************************
** Axion004
** 08/16/2015
**
** This program computes the value for Zeta(z) using a definite integral
** approximation through the Abel-Plana formula. The Abel-Plana formula
** can be shown to approximate the value for Zeta(s) through a definite
** integral. The integral approximation is handled through the Composite
** Simpson's Rule known as Adaptive Quadrature.
**************************************************************************/
import java.util.*;
import java.math.*;
public class AbelMain5 extends Complex {
private static MathContext MC = new MathContext(512,
RoundingMode.HALF_EVEN);
public static void main(String[] args) {
AbelMain();
}
// Main method
public static void AbelMain() {
double re = 0, im = 0;
double start, stop, totalTime;
Scanner scan = new Scanner(System.in);
System.out.println("Calculation of the Riemann Zeta " +
"Function in the form Zeta(s) = a + ib.");
System.out.println();
System.out.print("Enter the value of [a] inside the Riemann Zeta " +
"Function: ");
try {
re = scan.nextDouble();
}
catch (Exception e) {
System.out.println("Please enter a valid number for a.");
}
System.out.print("Enter the value of [b] inside the Riemann Zeta " +
"Function: ");
try {
im = scan.nextDouble();
}
catch (Exception e) {
System.out.println("Please enter a valid number for b.");
}
start = System.currentTimeMillis();
Complex z = new Complex(new BigDecimal(re), new BigDecimal(im));
System.out.println("The value for Zeta(s) is " + AbelPlana(z));
stop = System.currentTimeMillis();
totalTime = (double) (stop-start) / 1000.0;
System.out.println("Total time taken is " + totalTime + " seconds.");
}
/**
* The definite integral for Zeta(z) in the Abel-Plana formula.
* <br> Numerator = Sin(z * arctan(t))
* <br> Denominator = (1 + t^2)^(z/2) * (e^(2*pi*t) - 1)
* @param t - the value of t passed into the integrand.
* @param z - The complex value of z = a + i*b
* @return the value of the complex function.
*/
public static Complex f(double t, Complex z) {
Complex num = (z.multiply(Math.atan(t))).sin();
Complex D1 = new Complex(1 + t*t).pow(z.divide(TWO));
Complex D2 = new Complex(Math.pow(Math.E, 2.0*Math.PI*t) - 1.0);
Complex den = D1.multiply(D2);
return num.divide(den, MC);
}
/**
* Adaptive quadrature - See http://www.mathworks.com/moler/quad.pdf
* @param a - the lower bound of integration.
* @param b - the upper bound of integration.
* @param z - The complex value of z = a + i*b
* @return the approximate numerical value of the integral.
*/
public static Complex adaptiveQuad(double a, double b, Complex z) {
double EPSILON = 1E-10;
double step = b - a;
double c = (a + b) / 2.0;
double d = (a + c) / 2.0;
double e = (b + c) / 2.0;
Complex S1 = (f(a, z).add(f(c, z).multiply(FOUR)).add(f(b, z))).
multiply(step / 6.0);
Complex S2 = (f(a, z).add(f(d, z).multiply(FOUR)).add(f(c, z).multiply
(TWO)).add(f(e, z).multiply(FOUR)).add(f(b, z))).multiply
(step / 12.0);
Complex result = (S2.subtract(S1)).divide(FIFTEEN, MC);
if(S2.subtract(S1).mod() <= EPSILON)
return S2.add(result);
else
return adaptiveQuad(a, c, z).add(adaptiveQuad(c, b, z));
}
/**
* The definite integral for Zeta(z) in the Abel-Plana formula.
* <br> value = 1/2 + 1/(z-1) + 2 * Integral
* @param z - The complex value of z = a + i*b
* @return the value of Zeta(z) through value and the
* quadrature approximation.
*/
public static Complex AbelPlana(Complex z) {
Complex C1 = ONEHALF.add(ONE.divide(z.subtract(ONE), MC));
Complex C2 = TWO.multiply(adaptiveQuad(1E-16, 100.0, z));
if ( z.real().doubleValue() == 0 && z.imag().doubleValue() == 0)
return new Complex(0.0, 0.0);
else
return C1.add(C2);
}
}
комплексные числа (BigDecimal)
/**************************************************************************
**
** Complex Numbers
**
**************************************************************************
** Axion004
** 08/20/2015
**
** This class is necessary as a helper class for the calculation of
** imaginary numbers. The calculation of Zeta(z) inside AbelMain is in
** the form of z = a + i*b.
**************************************************************************/
import java.math.BigDecimal;
import java.math.MathContext;
import java.text.DecimalFormat;
import java.text.NumberFormat;
public class Complex extends Object{
private BigDecimal re;
private BigDecimal im;
/**
BigDecimal constant for zero
*/
final static Complex ZERO = new Complex(BigDecimal.ZERO) ;
/**
BigDecimal constant for one half
*/
final static Complex ONEHALF = new Complex(new BigDecimal(0.5));
/**
BigDecimal constant for one
*/
final static Complex ONE = new Complex(BigDecimal.ONE);
/**
BigDecimal constant for two
*/
final static Complex TWO = new Complex(new BigDecimal(2.0));
/**
BigDecimal constant for four
*/
final static Complex FOUR = new Complex(new BigDecimal(4.0)) ;
/**
BigDecimal constant for fifteen
*/
final static Complex FIFTEEN = new Complex(new BigDecimal(15.0)) ;
/**
Default constructor equivalent to zero
*/
public Complex() {
re = BigDecimal.ZERO;
im = BigDecimal.ZERO;
}
/**
Constructor with real part only
@param x Real part, BigDecimal
*/
public Complex(BigDecimal x) {
re = x;
im = BigDecimal.ZERO;
}
/**
Constructor with real part only
@param x Real part, double
*/
public Complex(double x) {
re = new BigDecimal(x);
im = BigDecimal.ZERO;
}
/**
Constructor with real and imaginary parts in double format.
@param x Real part
@param y Imaginary part
*/
public Complex(double x, double y) {
re= new BigDecimal(x);
im= new BigDecimal(y);
}
/**
Constructor for the complex number z = a + i*b
@param re Real part
@param im Imaginary part
*/
public Complex (BigDecimal re, BigDecimal im) {
this.re = re;
this.im = im;
}
/**
Real part of the Complex number
@return Re[z] where z = a + i*b.
*/
public BigDecimal real() {
return re;
}
/**
Imaginary part of the Complex number
@return Im[z] where z = a + i*b.
*/
public BigDecimal imag() {
return im;
}
/**
Complex conjugate of the Complex number
in which the conjugate of z is z-bar.
@return z-bar where z = a + i*b and z-bar = a - i*b
*/
public Complex conjugate() {
return new Complex(re, im.negate());
}
/**
* Returns the sum of this and the parameter.
@param augend the number to add
@param mc the context to use
@return this + augend
*/
public Complex add(Complex augend,MathContext mc)
{
//(a+bi)+(c+di) = (a + c) + (b + d)i
return new Complex(
re.add(augend.re,mc),
im.add(augend.im,mc));
}
/**
Equivalent to add(augend, MathContext.UNLIMITED)
@param augend the number to add
@return this + augend
*/
public Complex add(Complex augend)
{
return add(augend, MathContext.UNLIMITED);
}
/**
Addition of Complex number and a double.
@param d is the number to add.
@return z+d where z = a+i*b and d = double
*/
public Complex add(double d){
BigDecimal augend = new BigDecimal(d);
return new Complex(this.re.add(augend, MathContext.UNLIMITED),
this.im);
}
/**
* Returns the difference of this and the parameter.
@param subtrahend the number to subtract
@param mc the context to use
@return this - subtrahend
*/
public Complex subtract(Complex subtrahend, MathContext mc)
{
//(a+bi)-(c+di) = (a - c) + (b - d)i
return new Complex(
re.subtract(subtrahend.re,mc),
im.subtract(subtrahend.im,mc));
}
/**
* Equivalent to subtract(subtrahend, MathContext.UNLIMITED)
@param subtrahend the number to subtract
@return this - subtrahend
*/
public Complex subtract(Complex subtrahend)
{
return subtract(subtrahend,MathContext.UNLIMITED);
}
/**
Subtraction of Complex number and a double.
@param d is the number to subtract.
@return z-d where z = a+i*b and d = double
*/
public Complex subtract(double d){
BigDecimal subtrahend = new BigDecimal(d);
return new Complex(this.re.subtract(subtrahend, MathContext.UNLIMITED),
this.im);
}
/**
* Returns the product of this and the parameter.
@param multiplicand the number to multiply by
@param mc the context to use
@return this * multiplicand
*/
public Complex multiply(Complex multiplicand, MathContext mc)
{
//(a+bi)(c+di) = (ac - bd) + (ad + bc)i
return new Complex(
re.multiply(multiplicand.re,mc).subtract(im.multiply
(multiplicand.im,mc),mc),
re.multiply(multiplicand.im,mc).add(im.multiply
(multiplicand.re,mc),mc));
}
/**
Equivalent to multiply(multiplicand, MathContext.UNLIMITED)
@param multiplicand the number to multiply by
@return this * multiplicand
*/
public Complex multiply(Complex multiplicand)
{
return multiply(multiplicand,MathContext.UNLIMITED);
}
/**
Complex multiplication by a double.
@param d is the double to multiply by.
@return z*d where z = a+i*b and d = double
*/
public Complex multiply(double d){
BigDecimal multiplicand = new BigDecimal(d);
return new Complex(this.re.multiply(multiplicand, MathContext.UNLIMITED)
,this.im.multiply(multiplicand, MathContext.UNLIMITED));
}
/**
Modulus of a Complex number or the distance from the origin in
* the polar coordinate plane.
@return |z| where z = a + i*b.
*/
public double mod() {
if ( re.doubleValue() != 0.0 || im.doubleValue() != 0.0)
return Math.sqrt(re.multiply(re).add(im.multiply(im))
.doubleValue());
else
return 0.0;
}
/**
* Modulus of a Complex number squared
* @param z = a + i*b
* @return |z|^2 where z = a + i*b
*/
public double abs(Complex z) {
double doubleRe = re.doubleValue();
double doubleIm = im.doubleValue();
return doubleRe * doubleRe + doubleIm * doubleIm;
}
public Complex divide(Complex divisor)
{
return divide(divisor,MathContext.UNLIMITED);
}
/**
* The absolute value squared.
* @return The sum of the squares of real and imaginary parts.
* This is the square of Complex.abs() .
*/
public BigDecimal norm()
{
return re.multiply(re).add(im.multiply(im)) ;
}
/**
* The absolute value of a BigDecimal.
* @param mc amount of precision
* @return BigDecimal.abs()
*/
public BigDecimal abs(MathContext mc)
{
return BigDecimalMath.sqrt(norm(),mc) ;
}
/** The inverse of the the Complex number.
@param mc amount of precision
@return 1/this
*/
public Complex inverse(MathContext mc)
{
final BigDecimal hyp = norm() ;
/* 1/(x+iy)= (x-iy)/(x^2+y^2 */
return new Complex( re.divide(hyp,mc), im.divide(hyp,mc)
.negate() ) ;
}
/** Divide through another BigComplex number.
@param oth the other complex number
@param mc amount of precision
@return this/other
*/
public Complex divide(Complex oth, MathContext mc)
{
/* implementation: (x+iy)/(a+ib)= (x+iy)* 1/(a+ib) */
return multiply(oth.inverse(mc),mc) ;
}
/**
Division of Complex number by a double.
@param d is the double to divide
@return new Complex number z/d where z = a+i*b
*/
public Complex divide(double d){
BigDecimal divisor = new BigDecimal(d);
return new Complex(this.re.divide(divisor, MathContext.UNLIMITED),
this.im.divide(divisor, MathContext.UNLIMITED));
}
/**
Exponential of a complex number (z is unchanged).
<br> e^(a+i*b) = e^a * e^(i*b) = e^a * (cos(b) + i*sin(b))
@return exp(z) where z = a+i*b
*/
public Complex exp () {
return new Complex(Math.exp(re.doubleValue()) * Math.cos(im.
doubleValue()), Math.exp(re.doubleValue()) *
Math.sin(im.doubleValue()));
}
/**
The Argument of a Complex number or the angle in radians
with respect to polar coordinates.
<br> Tan(theta) = b / a, theta = Arctan(b / a)
<br> a is the real part on the horizontal axis
<br> b is the imaginary part of the vertical axis
@return arg(z) where z = a+i*b.
*/
public double arg() {
return Math.atan2(im.doubleValue(), re.doubleValue());
}
/**
The log or principal branch of a Complex number (z is unchanged).
<br> Log(a+i*b) = ln|a+i*b| + i*Arg(z) = ln(sqrt(a^2+b^2))
* + i*Arg(z) = ln (mod(z)) + i*Arctan(b/a)
@return log(z) where z = a+i*b
*/
public Complex log() {
return new Complex(Math.log(this.mod()), this.arg());
}
/**
The square root of a Complex number (z is unchanged).
Returns the principal branch of the square root.
<br> z = e^(i*theta) = r*cos(theta) + i*r*sin(theta)
<br> r = sqrt(a^2+b^2)
<br> cos(theta) = a / r, sin(theta) = b / r
<br> By De Moivre's Theorem, sqrt(z) = sqrt(a+i*b) =
* e^(i*theta / 2) = r(cos(theta/2) + i*sin(theta/2))
@return sqrt(z) where z = a+i*b
*/
public Complex sqrt() {
double r = this.mod();
double halfTheta = this.arg() / 2;
return new Complex(Math.sqrt(r) * Math.cos(halfTheta), Math.sqrt(r) *
Math.sin(halfTheta));
}
/**
The real cosh function for Complex numbers.
<br> cosh(theta) = (e^(theta) + e^(-theta)) / 2
@return cosh(theta)
*/
private double cosh(double theta) {
return (Math.exp(theta) + Math.exp(-theta)) / 2;
}
/**
The real sinh function for Complex numbers.
<br> sinh(theta) = (e^(theta) - e^(-theta)) / 2
@return sinh(theta)
*/
private double sinh(double theta) {
return (Math.exp(theta) - Math.exp(-theta)) / 2;
}
/**
The sin function for the Complex number (z is unchanged).
<br> sin(a+i*b) = cosh(b)*sin(a) + i*(sinh(b)*cos(a))
@return sin(z) where z = a+i*b
*/
public Complex sin() {
return new Complex(cosh(im.doubleValue()) * Math.sin(re.doubleValue()),
sinh(im.doubleValue())* Math.cos(re.doubleValue()));
}
/**
The cos function for the Complex number (z is unchanged).
<br> cos(a +i*b) = cosh(b)*cos(a) + i*(-sinh(b)*sin(a))
@return cos(z) where z = a+i*b
*/
public Complex cos() {
return new Complex(cosh(im.doubleValue()) * Math.cos(re.doubleValue()),
-sinh(im.doubleValue()) * Math.sin(re.doubleValue()));
}
/**
The hyperbolic sin of the Complex number (z is unchanged).
<br> sinh(a+i*b) = sinh(a)*cos(b) + i*(cosh(a)*sin(b))
@return sinh(z) where z = a+i*b
*/
public Complex sinh() {
return new Complex(sinh(re.doubleValue()) * Math.cos(im.doubleValue()),
cosh(re.doubleValue()) * Math.sin(im.doubleValue()));
}
/**
The hyperbolic cosine of the Complex number (z is unchanged).
<br> cosh(a+i*b) = cosh(a)*cos(b) + i*(sinh(a)*sin(b))
@return cosh(z) where z = a+i*b
*/
public Complex cosh() {
return new Complex(cosh(re.doubleValue()) *Math.cos(im.doubleValue()),
sinh(re.doubleValue()) * Math.sin(im.doubleValue()));
}
/**
The tan of the Complex number (z is unchanged).
<br> tan (a+i*b) = sin(a+i*b) / cos(a+i*b)
@return tan(z) where z = a+i*b
*/
public Complex tan() {
return (this.sin()).divide(this.cos());
}
/**
The arctan of the Complex number (z is unchanged).
<br> tan^(-1)(a+i*b) = 1/2 i*(log(1-i*(a+b*i))-log(1+i*(a+b*i))) =
<br> -1/2 i*(log(i*a - b+1)-log(-i*a + b+1))
@return arctan(z) where z = a+i*b
*/
public Complex atan(){
Complex ima = new Complex(0.0,-1.0); //multiply by negative i
Complex num = new Complex(this.re.doubleValue(),this.im.doubleValue()
-1.0);
Complex den = new Complex(this.re.negate().doubleValue(),this.im
.negate().doubleValue()-1.0);
Complex two = new Complex(2.0, 0.0); // divide by 2
return ima.multiply(num.divide(den).log()).divide(two);
}
/**
* The Math.pow equivalent of two Complex numbers.
* @param z - the complex base in the form z = a + i*b
* @return z^y where z = a + i*b and y = c + i*d
*/
public Complex pow(Complex z){
Complex a = z.multiply(this.log(), MathContext.UNLIMITED);
return a.exp();
}
/**
* The Math.pow equivalent of a Complex number to the power
* of a double.
* @param d - the double to be taken as the power.
* @return z^d where z = a + i*b and d = double
*/
public Complex pow(double d){
Complex a=(this.log()).multiply(d);
return a.exp();
}
/**
Override the .toString() method to generate complex numbers, the
* string representation is now a literal Complex number.
@return a+i*b, a-i*b, a, or i*b as desired.
*/
public String toString() {
NumberFormat formatter = new DecimalFormat();
formatter = new DecimalFormat("#.###############E0");
if (re.doubleValue() != 0.0 && im.doubleValue() > 0.0) {
return formatter.format(re) + " + " + formatter.format(im)
+"*i";
}
if (re.doubleValue() !=0.0 && im.doubleValue() < 0.0) {
return formatter.format(re) + " - "+ formatter.format(im.negate())
+ "*i";
}
if (im.doubleValue() == 0.0) {
return formatter.format(re);
}
if (re.doubleValue() == 0.0) {
return formatter.format(im) + "*i";
}
return formatter.format(re) + " + i*" + formatter.format(im);
}
}
я рассматриваю ответ ниже.
одна проблема может быть из-за
Complex num = (z.multiply(Math.atan(t))).sin();
Complex D1 = new Complex(1 + t*t).pow(z.divide(TWO));
Complex D2 = new Complex(Math.pow(Math.E, 2.0*Math.PI*t) - 1.0);
Complex den = D1.multiply(D2, MathContext.UNLIMITED);
я не подаю заявление BigDecimal.pow(BigDecimal). Хотя, я не думаю, что это прямая проблема, которая заставляет арифметику с плавающей запятой создавать различия.
Edit: я попробовал новое интегральное приближение дзета-функции. В конечном счете, я разработаю новый метод расчета BigDecimal.pow(BigDecimal).
3 ответов
предостережение я согласен со всеми комментариями в ответ@laune, но у меня такое впечатление, что вы, возможно, захотите продолжить это в любом случае. Убедитесь особенно, что вы действительно понимаете 1) и что это значит для вас - очень легко сделать много тяжелых вычислений, чтобы получить бессмысленные результаты.
произвольные функции с плавающей запятой точности в Java
повторить немного, я думаю, что ваша проблема действительно, с математикой и численным методом, который вы выбрали, но вот реализация с использованием библиотека Apfloat. Я настоятельно призываю вас использовать готовую библиотеку произвольной точности (или аналогичную), поскольку она позволяет избежать необходимости "свернуть ваши собственные" функции произвольной точности (например,pow, exp,sin, atan и т. д.). Ты говоришь
в конечном счете, я разработаю новый метод расчета У bigdecimal.pow (BigDecimal)
это действительно трудно сделать это правильно.
вам также нужно следить за точностью ваших констант-обратите внимание, что я использую реализацию образца Apfloat для вычисления PI к большому числу (для некоторого определения большого!) сига фиг. Я до некоторой степени верю, что библиотека Apfloat использует достаточно точные значения для e in exponentiation-источник доступен, если вы хотите проверять.
разное интегральные формулировки для расчета Дзета
вы ставите три различных метода интеграции на основе в одном из ваших изменений:

Тот, который помечен 25.5.12, является тем, который у вас в настоящее время есть в вопросе, и (хотя это можно легко вычислить на нуле), трудно работать с из-за 2) в ответ@laune. Я реализовал 25.5.12 как integrand1() в коде - я призываю вас, чтобы построить его с диапазон t по-разному s = a + 0i и понять, как он ведет себя. Или посмотрите на сюжеты в статьи Дзета о компании Wolfram mathworld. Один маркирован 25.5.11 я реализовал через integrand2() и код в конфигурации, которую я публикую ниже.
код
хотя я немного неохотно размещать код, который, несомненно, найдет неправильные результаты в некоторых конфигурациях из - за всех вышеперечисленных вещей- я закодировал то, что вы пытаетесь сделать ниже, используя произвольные прецизионные объекты с плавающей запятой для переменных.
если вы хотите изменить, какую формулировку Вы используете (например, с 25.5.11 до 25.5.12), вы можете изменить, какой integrand функция обертки f() возвращает или, еще лучше, изменить adaptiveQuad принять произвольный метод интеграла, обернутый в class с интерфейсом... Вам также придется изменить арифметику в findZeta() если вы хотите использовать один из других интегральных формулировок.
играть с константы в начале, сколько душе угодно. Я не тестировал много комбинаций, так как думаю, что математические проблемы здесь переопределяют программные.
я оставил его, чтобы сделать 2+3i в около 2000 звонков адаптивный метод quadature и матч первые 15 или около того цифр значения Вольфрам.
я проверил, что он все еще работает с PRECISION = 120l и EPSILON=1e-15. Программа соответствует Wolfram alpha в первых 18 или около того значимых цифрах для трех тестовых случаев вы обеспечиваете. Последний (230+30i) занимает много времени даже на быстром компьютере - он вызывает integrand fucntion около 100,000+ раз. Обратите внимание, что я использую 40 значение INFINITY в Интеграле-не очень высокие, но более высокие значения показывают задачу 1)Как уже обсуждалось...
Б. Н. это не быстро (вы будете измерять в минутах или часах, а не секундах, но вы получите очень быстро, если хотите согласиться с тем, что 10^-15 ~= 10^-70, как большинство людей!!). Это даст вам несколько цифр, которые соответствуют Wolfram Alpha ;) вы можете взять PRECISION до 20, INFINITY до 10 и EPSILON to 1e-10 чтобы проверить несколько результатов с помощью small s первый... Я в какой-то печати, поэтому он говорит вам каждый 100-й раз adaptiveQuad вызывается для комфорта.
подтверждение однако хорошая ваша точность - она не собирается преодолевать математические характеристики функций, участвующих в этом способе вычисления Дзета. Я!--39-->сильно сомневаюсь так, например, делает Wolfram alpha. Посмотрите методы суммирования рядов, если вам нужны более сговорчивые методы.
import java.io.PrintWriter;
import org.apfloat.ApcomplexMath;
import org.apfloat.Apcomplex;
import org.apfloat.Apfloat;
import org.apfloat.samples.Pi;
public class ZetaFinder
{
//Number of sig figs accuracy. Note that infinite should be reserved
private static long PRECISION = 40l;
// Convergence criterion for integration
static Apfloat EPSILON = new Apfloat("1e-15",PRECISION);
//Value of PI - enhanced using Apfloat library sample calculation of Pi in constructor,
//Fast enough that we don't need to hard code the value in.
//You could code hard value in for perf enhancement
static Apfloat PI = null; //new Apfloat("3.14159");
//Integration limits - I found too high a value for "infinity" causes integration
//to terminate on first iteration. Plot the integrand to see why...
static Apfloat INFINITE_LIMIT = new Apfloat("40",PRECISION);
static Apfloat ZERO_LIMIT = new Apfloat("1e-16",PRECISION); //You can use zero for the 25.5.12
static Apfloat one = new Apfloat("1",PRECISION);
static Apfloat two = new Apfloat("2",PRECISION);
static Apfloat four = new Apfloat("4",PRECISION);
static Apfloat six = new Apfloat("6",PRECISION);
static Apfloat twelve = new Apfloat("12",PRECISION);
static Apfloat fifteen = new Apfloat("15",PRECISION);
static int counter = 0;
Apcomplex s = null;
public ZetaFinder(Apcomplex s)
{
this.s = s;
Pi.setOut(new PrintWriter(System.out, true));
Pi.setErr(new PrintWriter(System.err, true));
PI = (new Pi.RamanujanPiCalculator(PRECISION+10, 10)).execute(); //Get Pi to a higher precision than integer consts
System.out.println("Created a Zeta Finder based on Abel-Plana for s="+s.toString() + " using PI="+PI.toString());
}
public static void main(String[] args)
{
Apfloat re = new Apfloat("2", PRECISION);
Apfloat im = new Apfloat("3", PRECISION);
Apcomplex s = new Apcomplex(re,im);
ZetaFinder finder = new ZetaFinder(s);
System.out.println(finder.findZeta());
}
private Apcomplex findZeta()
{
Apcomplex retval = null;
//Method currently in question (a.k.a. 25.5.12)
//Apcomplex mult = ApcomplexMath.pow(two, this.s);
//Apcomplex firstterm = (ApcomplexMath.pow(two, (this.s.add(one.negate())))).divide(this.s.add(one.negate()));
//Easier integrand method (a.k.a. 25.5.11)
Apcomplex mult = two;
Apcomplex firstterm = (one.divide(two)).add(one.divide(this.s.add(one.negate())));
Apfloat limita = ZERO_LIMIT;//Apfloat.ZERO;
Apfloat limitb = INFINITE_LIMIT;
System.out.println("Trying to integrate between " + limita.toString() + " and " + limitb.toString());
Apcomplex integral = adaptiveQuad(limita, limitb);
retval = firstterm.add((mult.multiply(integral)));
return retval;
}
private Apcomplex adaptiveQuad(Apfloat a, Apfloat b) {
//if (counter % 100 == 0)
{
System.out.println("In here for the " + counter + "th time");
}
counter++;
Apfloat h = b.add(a.negate());
Apfloat c = (a.add(b)).divide(two);
Apfloat d = (a.add(c)).divide(two);
Apfloat e = (b.add(c)).divide(two);
Apcomplex Q1 = (h.divide(six)).multiply(f(a).add(four.multiply(f(c))).add(f(b)));
Apcomplex Q2 = (h.divide(twelve)).multiply(f(a).add(four.multiply(f(d))).add(two.multiply(f(c))).add(four.multiply(f(e))).add(f(b)));
if (ApcomplexMath.abs(Q2.add(Q1.negate())).compareTo(EPSILON) < 0)
{
System.out.println("Returning");
return Q2.add((Q2.add(Q1.negate())).divide(fifteen));
}
else
{
System.out.println("Recursing with intervals "+a+" to " + c + " and " + c + " to " +d);
return adaptiveQuad(a, c).add(adaptiveQuad(c, b));
}
}
private Apcomplex f(Apfloat x)
{
return integrand2(x);
}
/*
* Simple test integrand (z^2)
*
* Can test implementation by asserting that the adaptiveQuad
* with this function evaluates to z^3 / 3
*/
private Apcomplex integrandTest(Apfloat t)
{
return ApcomplexMath.pow(t, two);
}
/*
* Abel-Plana formulation integrand
*/
private Apcomplex integrand1(Apfloat t)
{
Apcomplex numerator = ApcomplexMath.sin(this.s.multiply(ApcomplexMath.atan(t)));
Apcomplex bottomlinefirstbr = one.add(ApcomplexMath.pow(t, two));
Apcomplex D1 = ApcomplexMath.pow(bottomlinefirstbr, this.s.divide(two));
Apcomplex D2 = (ApcomplexMath.exp(PI.multiply(t))).add(one);
Apcomplex denominator = D1.multiply(D2);
Apcomplex retval = numerator.divide(denominator);
//System.out.println("Integrand evaluated at "+t+ " is "+retval);
return retval;
}
/*
* Abel-Plana formulation integrand 25.5.11
*/
private Apcomplex integrand2(Apfloat t)
{
Apcomplex numerator = ApcomplexMath.sin(this.s.multiply(ApcomplexMath.atan(t)));
Apcomplex bottomlinefirstbr = one.add(ApcomplexMath.pow(t, two));
Apcomplex D1 = ApcomplexMath.pow(bottomlinefirstbr, this.s.divide(two));
Apcomplex D2 = ApcomplexMath.exp(two.multiply(PI.multiply(t))).add(one.negate());
Apcomplex denominator = D1.multiply(D2);
Apcomplex retval = numerator.divide(denominator);
//System.out.println("Integrand evaluated at "+t+ " is "+retval);
return retval;
}
}
замечание о "правильности"
обратите внимание, что в вашем ответе - вы призываете zeta(2+3i) и zeta(100) "правильно" по сравнению с Wolfram, когда они показывают ошибки ~1e-10 и ~1e-9 соответственно (они отличаются 10-м и 9-м десятичным разрядом), но вы беспокоитесь о zeta(230+30i) потому что он обладает погрешностью порядка!--34--> в воображаемой составляющей (38e-15 vs 5e-70 которые оба очень близки к нулю). Таким образом, в некотором смысле то, что вы называете "неправильным", ближе к значению вольфрама, чем те, которые вы называете "правильными". Может быть, вы беспокоитесь, что ведущие цифры разные, но это на самом деле не мера точности там.
Конечная нота
если вы не делаете это, чтобы узнать о том, как функции ведут себя и как точность с плавающей запятой взаимодействует с ним - не делай так!--41-->. Даже собственная документация Apfloat говорит:
этот пакет конструирован для весьма точности. Результат может быть на несколько цифр меньше, чем вы ожидали (около 10) и последние несколько (около 10) цифры в ther результат может быть неточным. Если вы планируете использовать числа всего с несколькими сотнями цифр, используйте такую программу, как PARI (это бесплатно и доступно отftp://megrez.math.u-bordeaux.fr) или a коммерческая программа, такая как Mathematica или Maple, если это возможно.
я бы добавил mpmath в python в этот список в качестве бесплатной альтернативы сейчас.
(1) интеграция использует adaptQuad, начиная с интервала [0,10]. Для z=a+ib со все более большими значениями a и b=0 Интеграл является все более колебательной функцией, причем число нулей только в [0,5] пропорционально a и возрастает до 43 при z=100.
поэтому начинать аппроксимацию с интервала, включающего один или несколько нулей, рискованно,так как программа, как показано довольно ясно. При z=100 Интеграл равен 0, -2.08 E-78 и 7.12 E-115 при 0, 5 и 10, соответственно. Поэтому сравнение результата Формулы Симпсона с 1e-20 возвращает true, а результат абсолютно неверен.
(2) вычисление в методе AbelPlana включает в себя два комплексных числа, C1 и C2. Для z=a+0i они реальны, и в таблице ниже показаны их значения для различных значений a:
a C1 C2
10 5.689E1 1.024E3
20 2.759E4 1.048E6
30 1.851E7 1.073E9
40 1.409E10 1.099E12
60 9.770E15 1.152E18
100 6.402E27 1.267E30
теперь мы знаем, что значения ζ (a+0i) уменьшаются к 1 для увеличения a. Очевидно, что для двух значений выше 1E15 невозможно произведите содержательный результат около одного вычитанный от Одина другого.
таблица также предполагает, что для хорошего результата ζ(a+0i) с помощью этого алгоритма C1 и C2*I (i-Интеграл) должны быть вычислены с точностью около 45 значащих цифр. (Произвольная математика точности не избегает ловушки, описанной в (1).)
(3) Обратите внимание, что при использовании библиотеки с произвольной точностью такие значения E и PI должны предоставляться с большей точностью, чем двойные значения в Java.ленг.Математика может предложить.
редактировать (25.5.11) имеет столько же нулей в [0,10] как (25.5.12). Вычисление в 0 сложно, но это не сингулярность. Это позволяет избежать проблемы (2).
для ответа относительно использования произвольной арифметики точности с интегральным методом, описанным в OP-см. my другого ответа
, я заинтригован этим и подумал, что метод суммы рядов должен быть более численно стабильным. Я нашел представление рядов Дирихле на Википедии и реализовал его (полностью работоспособный код ниже).
это дало мне интересную информацию. Если я установлю сходимость EPSILON to 1e-30 Я ровно те же цифры и показатель (т. е. 1e-70 в воображаемой части) как вольфрам для zeta(100) и zeta(230+ 30i) и алгоритм завершается только после добавления 1 или 2 терминов к сумме. Это наводит меня на две мысли:--13-->
- Wolfram alpha использует этот метод sum или что-то подобное для вычисления возвращаемых значений.
- "правильный" - ness эти ценности трудно оценить. Например, zeta (100) имеет точное значение в терминах PI, поэтому его можно судить. Я не знаю, является ли эта оценка
zeta(230+30i)лучше или хуже, чем тот, который найден интегральным методом - этот метод действительно довольно медленно сходится к
zeta(2+3i)и, возможно, потребуетсяEPSILONпринимая ниже для использования.
я нашел научные статьи это компендиум числовых методов для вычисления zeta. Этот указывает мне, что основная проблема здесь, безусловно, "нетривиальна"!!
в любом случае-я оставляю реализацию суммы серии здесь в качестве альтернативы для тех, кто может столкнуться с ней в будущем.
import java.io.PrintWriter;
import org.apfloat.ApcomplexMath;
import org.apfloat.Apcomplex;
import org.apfloat.Apfloat;
import org.apfloat.ApfloatMath;
import org.apfloat.samples.Pi;
public class ZetaSeries {
//Number of sig figs accuracy. Note that infinite should be reserved
private static long PRECISION = 100l;
// Convergence criterion for integration
static Apfloat EPSILON = new Apfloat("1e-30",PRECISION);
static Apfloat one = new Apfloat("1",PRECISION);
static Apfloat two = new Apfloat("2",PRECISION);
static Apfloat minus_one = one.negate();
static Apfloat three = new Apfloat("3",PRECISION);
private Apcomplex s = null;
private Apcomplex s_plus_two = null;
public ZetaSeries(Apcomplex s) {
this.s = s;
this.s_plus_two = two.add(s);
}
public static void main(String[] args) {
Apfloat re = new Apfloat("230", PRECISION);
Apfloat im = new Apfloat("30", PRECISION);
Apcomplex s = new Apcomplex(re,im);
ZetaSeries z = new ZetaSeries(s);
System.out.println(z.findZeta());
}
private Apcomplex findZeta() {
Apcomplex series_sum = Apcomplex.ZERO;
Apcomplex multiplier = (one.divide(this.s.add(minus_one)));
int stop_condition = 1;
long n = 1;
while (stop_condition > 0)
{
Apcomplex term_to_add = sum_term(n);
stop_condition = ApcomplexMath.abs(term_to_add).compareTo(EPSILON);
series_sum = series_sum.add(term_to_add);
//if(n%50 == 0)
{
System.out.println("At iteration " + n + " : " + multiplier.multiply(series_sum));
}
n+=1;
}
return multiplier.multiply(series_sum);
}
private Apcomplex sum_term(long n_long) {
Apfloat n = new Apfloat(n_long, PRECISION);
Apfloat n_plus_one = n.add(one);
Apfloat two_n = two.multiply(n);
Apfloat t1 = (n.multiply(n_plus_one)).divide(two);
Apcomplex t2 = (two_n.add(three).add(this.s)).divide(ApcomplexMath.pow(n_plus_one,s_plus_two));
Apcomplex t3 = (two_n.add(minus_one).add(this.s.negate())).divide(ApcomplexMath.pow(n,this.s_plus_two));
return t1.multiply(t2.add(t3.negate()));
}
}