преобразование геодезических расстояний в python
в python есть на scipy.ndimage.morphology модуль. Я применил его к простому случаю, чтобы вычислить расстояние от одной ячейки в маскированном массиве numpy.
однако функция удаляет маску массива и вычисляет, как и ожидалось, евклидово расстояние для каждой ячейки с ненулевым значением из опорной ячейки с нулевым значением.
Ниже приведен пример, который я дал в мой блог пост:
%pylab
from scipy.ndimage.morphology import distance_transform_edt
l = 100
x, y = np.indices((l, l))
center1 = (50, 20)
center2 = (28, 24)
center3 = (30, 50)
center4 = (60,48)
radius1, radius2, radius3, radius4 = 15, 12, 19, 12
circle1 = (x - center1[0])**2 + (y - center1[1])**2 < radius1**2
circle2 = (x - center2[0])**2 + (y - center2[1])**2 < radius2**2
circle3 = (x - center3[0])**2 + (y - center3[1])**2 < radius3**2
circle4 = (x - center4[0])**2 + (y - center4[1])**2 < radius4**2
# 3 circles
img = circle1 + circle2 + circle3 + circle4
mask = ~img.astype(bool)
img = img.astype(float)
m = ones_like(img)
m[center1] = 0
#imshow(distance_transform_edt(m), interpolation='nearest')
m = ma.masked_array(distance_transform_edt(m), mask)
imshow(m, interpolation='nearest')

однако я хочу вычислить преобразование геодезического расстояния, которое учитывает маскированные элементы массива. Я не хочу вычислять евклидово расстояние вдоль прямой линии, проходящей через замаскированные элементы.
я использовал алгоритм Dijkstra для получения результата, который я хочу. Ниже приведена реализация, которую я предложил:
def geodesic_distance_transform(m):
mask = m.mask
visit_mask = mask.copy() # mask visited cells
m = m.filled(numpy.inf)
m[m!=0] = numpy.inf
distance_increments = numpy.asarray([sqrt(2), 1., sqrt(2), 1., 1., sqrt(2), 1., sqrt(2)])
connectivity = [(i,j) for i in [-1, 0, 1] for j in [-1, 0, 1] if (not (i == j == 0))]
cc = unravel_index(m.argmin(), m.shape) # current_cell
while (~visit_mask).sum() > 0:
neighbors = [tuple(e) for e in asarray(cc) - connectivity
if not visit_mask[tuple(e)]]
tentative_distance = [distance_increments[i] for i,e in enumerate(asarray(cc) - connectivity)
if not visit_mask[tuple(e)]]
for i,e in enumerate(neighbors):
d = tentative_distance[i] + m[cc]
if d < m[e]:
m[e] = d
visit_mask[cc] = True
m_mask = ma.masked_array(m, visit_mask)
cc = unravel_index(m_mask.argmin(), m.shape)
return m
gdt = geodesic_distance_transform(m)
imshow(gdt, interpolation='nearest')
colorbar()
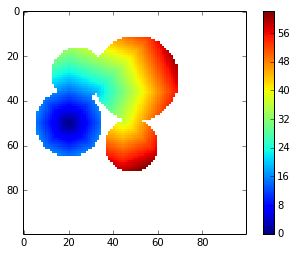
функция, реализованная выше, хорошо работает но слишком медленно для приложения, которое я разработал, которому нужно вычислить преобразование геодезического расстояния несколько раз.
Ниже приведен временной ориентир евклидова преобразования расстояния и геодезического преобразования расстояния:
%timeit distance_transform_edt(m)
1000 loops, best of 3: 1.07 ms per loop
%timeit geodesic_distance_transform(m)
1 loops, best of 3: 702 ms per loop
как я могу получить более быстрое преобразование геодезического расстояния?
3 ответов
прежде всего, спасибо за очень ясный и хорошо написанный вопрос.
существует очень хорошая и быстрая реализация Fast Marching метод scikit-fmm чтобы решить эту проблему. Подробности можно найти здесь:
http://pythonhosted.org//scikit-fmm/
установка может быть самой сложной частью, но в Windows с Conda ее легко, так как есть 64-битный пакет Conda для Py27: https://binstar.org/jmargeta/scikit-fmm
оттуда просто передайте ему свой маскированный массив, как вы это делаете со своей собственной функцией. Например:
distance = skfmm.distance(m)
результаты выглядят похожими, и я думаю, даже немного лучше. Ваш подход ищет (по-видимому) в восьми различных направлениях, что приводит к некоторому "восьмиугольному" расстоянию.
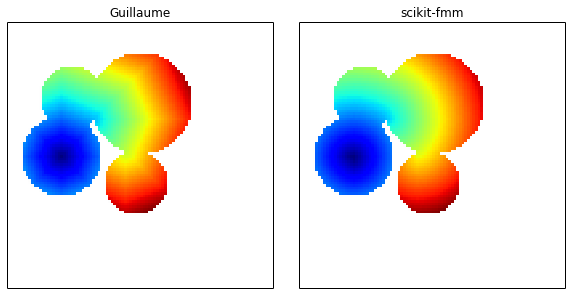
на моей машине реализация scikit-fmm превышает 200x быстрее, чем ваша функция.

немного быстрее (около 10x) реализация, которая достигает того же результата, что и ваш geodesic_distance_transform:
def getMissingMask(slab):
nan_mask=numpy.where(numpy.isnan(slab),1,0)
if not hasattr(slab,'mask'):
mask_mask=numpy.zeros(slab.shape)
else:
if slab.mask.size==1 and slab.mask==False:
mask_mask=numpy.zeros(slab.shape)
else:
mask_mask=numpy.where(slab.mask,1,0)
mask=numpy.where(mask_mask+nan_mask>0,1,0)
return mask
def geodesic(img,seed):
seedy,seedx=seed
mask=getMissingMask(img)
#----Call distance_transform_edt if no missing----
if mask.sum()==0:
slab=numpy.ones(img.shape)
slab[seedy,seedx]=0
return distance_transform_edt(slab)
target=(1-mask).sum()
dist=numpy.ones(img.shape)*numpy.inf
dist[seedy,seedx]=0
def expandDir(img,direction):
if direction=='n':
l1=img[0,:]
img=numpy.roll(img,1,axis=0)
img[0,:]==l1
elif direction=='s':
l1=img[-1,:]
img=numpy.roll(img,-1,axis=0)
img[-1,:]==l1
elif direction=='e':
l1=img[:,0]
img=numpy.roll(img,1,axis=1)
img[:,0]=l1
elif direction=='w':
l1=img[:,-1]
img=numpy.roll(img,-1,axis=1)
img[:,-1]==l1
elif direction=='ne':
img=expandDir(img,'n')
img=expandDir(img,'e')
elif direction=='nw':
img=expandDir(img,'n')
img=expandDir(img,'w')
elif direction=='sw':
img=expandDir(img,'s')
img=expandDir(img,'w')
elif direction=='se':
img=expandDir(img,'s')
img=expandDir(img,'e')
return img
def expandIter(img):
sqrt2=numpy.sqrt(2)
tmps=[]
for dirii,dd in zip(['n','s','e','w','ne','nw','sw','se'],\
[1,]*4+[sqrt2,]*4):
tmpii=expandDir(img,dirii)+dd
tmpii=numpy.minimum(tmpii,img)
tmps.append(tmpii)
img=reduce(lambda x,y:numpy.minimum(x,y),tmps)
return img
#----------------Iteratively expand----------------
dist_old=dist
while True:
expand=expandIter(dist)
dist=numpy.where(mask,dist,expand)
nc=dist.size-len(numpy.where(dist==numpy.inf)[0])
if nc>=target or numpy.all(dist_old==dist):
break
dist_old=dist
return dist
также обратите внимание, что если маска образует более 1 связанных областей (например, добавление другого круга, не касаясь других), ваша функция попадет в бесконечный цикл.
обновление:
я нашел одну реализацию на Cython быстрых радикальных метода в этот ноутбук, которое можно использовать для того чтобы достигнуть такого же результата как scikit-fmm С, вероятно, сравнимой скорости. Нужно просто подать матрицу двоичного флага (с 1S в качестве жизнеспособных точек,inf иное) в
