Преобразование переменной плотности по логарифмической шкале C R

Я хочу построить плотность переменной, диапазон которой следующий:

 Min.   :-1214813.0  
 1st Qu.:       1.0  
 Median :      40.0  
 Mean   :     303.2  
 3rd Qu.:     166.0  
 Max.   : 1623990.0

линейный график плотности приводит к высокому столбцу в диапазоне [0,1000], с двумя очень длинными хвостами к положительной бесконечности и отрицательной бесконечности. Поэтому я хотел бы преобразовать переменную в логарифмическую шкалу, чтобы увидеть, что происходит вокруг среднего. Например, я думаю о чем-то вроде:

log_values = c( -log10(-values[values<0]), log10(values[values>0]))

что приводит к:

Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
-6.085   0.699   1.708   1.286   2.272   6.211

главная проблема с этим заключается в том, что он не включает 0 значения. Конечно, я могу сдвинуть все значения от 0С values[values>=0]+1, но это приведет к некоторому искажению данных.

каким был бы принятый и научно обоснованный способ преобразования этой переменной в логарифмическую шкалу?

6
logarithm r scale

3 ответов

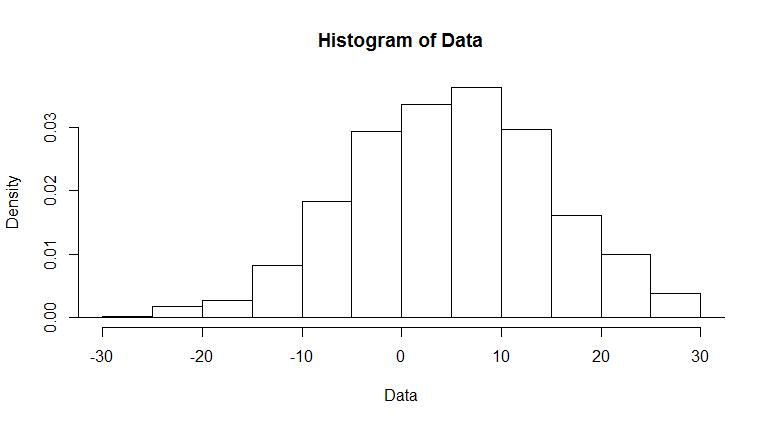
помимо преобразования, вы можете манипулировать собой гистограмму, чтобы получить представление о ваших данных. Это дает вам преимущество в том, что сами сюжеты остаются читаемыми, и вы получаете немедленное представление о распределении в центре. Скажем, мы моделируем следующие данные:

Data <- c(rnorm(1000,5,10),sample(-10000:10000,10))
> summary(Data)
     Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
-9669.000    -2.119     5.332    85.430    12.460  9870.000

тогда у вас есть несколько разных подходов. Проще всего увидеть, что происходит в центре ваших данных, это просто построить центр ваших данных. В этом случае скажите, что меня интересует, что происходит между первой и третьей квартилями я могу построить график:--8--> 

hist(Data,
     xlim=c(-30,30),
     breaks=c(min(Data),seq(-30,30,by=5),max(Data))
     main="Center of Data"
     )

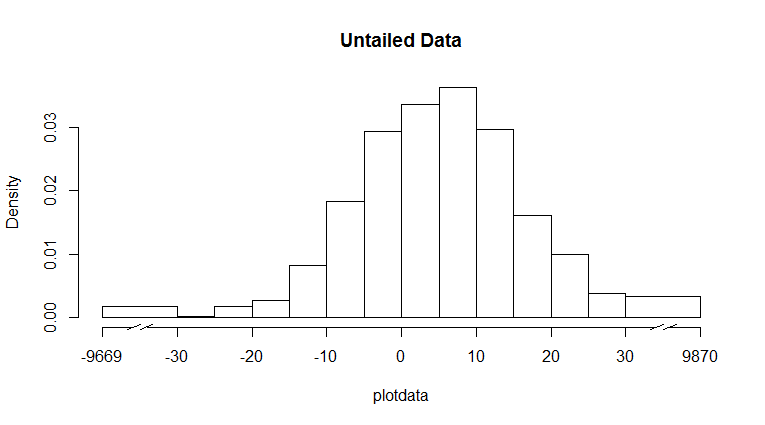
enter image description here

если вы также хотите подсчитать хвосты, вы можете преобразовать свои данные, чтобы свернуть хвосты и изменить ось, чтобы отразить это, следующим образом:

  1. вы назначаете все значения за пределами диапазона интересов значение, которое находится за пределами этого диапазона
  2. вы строите гистограмму, связывая все экстремальные значения в одном bin
  3. вы строите ось X с помощью правильные метки
  4. вы используете axis.break() из пакета plotrix чтобы добавить некоторые разрывы на оси X, указывая прерывистую ось

для этого вы можете использовать что-то вроде следующего кода:

 require(plotrix)
 # rearrange data
 plotdata <- Data
 id <- plotdata < -30 | plotdata > 30
 plotdata[id] <- sign(plotdata[id])*35
 # plot histogram
 hist(plotdata,
      xlim=c(-40,40),
      breaks=c(-40,seq(-30,30,by=5),40),
      main="Untailed Data",
      xaxt='n'   # leave the X axis away
      )
 # Construct the X axis
 axis(1,
      at=c(-40,seq(-30,30,by=10),40),
      labels=c(min(Data),seq(-30,30,by=10),max(Data))
 )
 # add axis breaks
 axis.break(axis=1,breakpos=-35)
 axis.break(axis=1,breakpos=35)

это дает вам :

enter image description here

обратите внимание, что вы получаете сырые частоты, добавив freq=TRUE до

3

то, что у вас есть, по сути, то, что предлагает @James. Это проблематично для значений в (-1,1), особенно ближе к нулю:

x <- seq(-2, 2, by=.01)
plot(x, sign(x)*log10(abs(x)), pch='.')

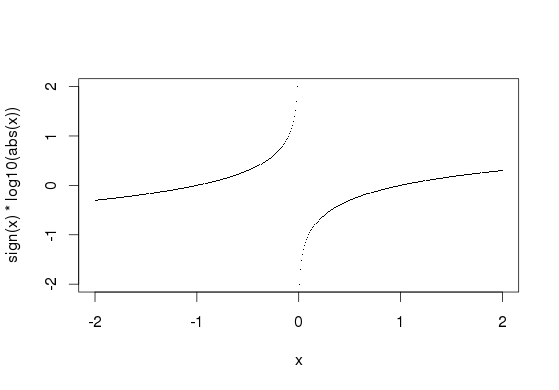
enter image description here

что-то вроде этого может помочь:

y <- c(-log10(-x[x<(-1)])-1, x[x >= -1 & x <= 1], log10(x[x>1])+1)

plot(x, y, pch='.')

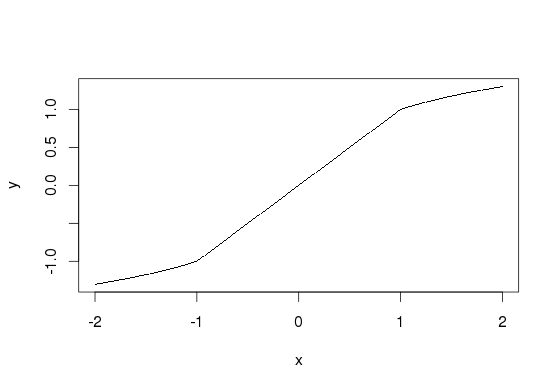
enter image description here

это непрерывный. Можно заставить c^1, используя интервал (-1 / log (10), 1/log(10)), который найден путем решения D/dx log10(x) = 1 :

z <- c( -log10(-x[x<(-1/log(10))]) - 1/log(10)+log10(1/log(10)),
         x[x >= -1/log(10) & x <= 1/log(10)],
         log10(x[x>1/log(10)]) + 1/log(10)-log10(1/log(10))
       )
plot(x, z, pch='.')

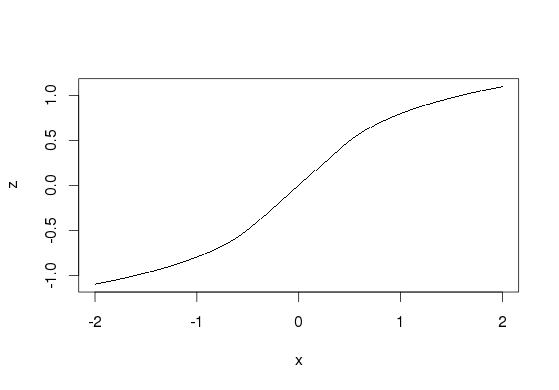
enter image description here

4

Я добавляю это как еще один ответ, потому что, хотя идея похожа, сопоставление принципиально отличается.

когда небольшие значения (log(1 + .), а не log(.).

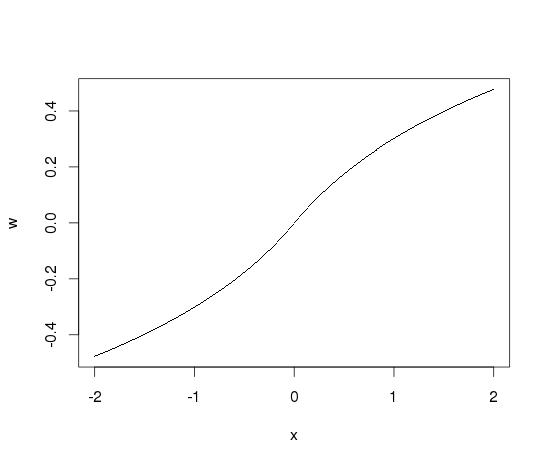
отразить через происхождение, и мы получаем что-то полезное:

x <- seq(-2, 2, by=.01)   
w <- c( -log10(1-x[x<0]), x[x==0], log10(1+x[x>0]))

plot(x, w, pch='.')

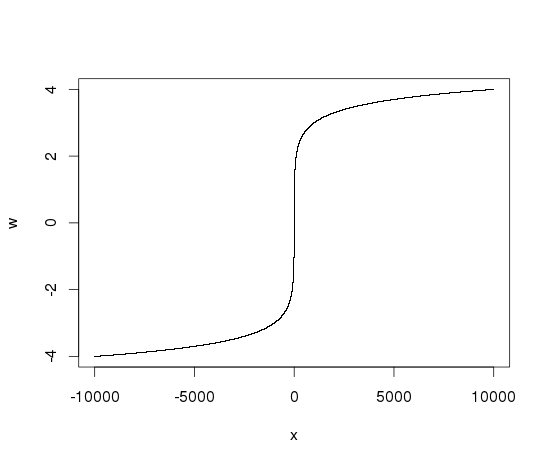
должно быть ясно, что функция гладкая, так как направленные производные вокруг 0 также будут отражены. enter image description here

С гораздо большие значения в X:

x <- seq(-10000, 10000, by=.01)
w <- c( -log10(1-x[x<0]), x[x==0], log10(1+x[x>0]))
plot(x, w, pch='.')

enter image description here

1