Преобразование строки в строку палиндрома с минимальными вставками

чтобы найти минимальное количество вставок, необходимых для преобразования данной строки(строк) в палиндром, я нахожу самую длинную общую подпоследовательность строки(lcs_string) и ее обратную. Поэтому количество вставок должно быть сделано length(s) - length (lcs_string)

какой метод следует использовать для поиска эквивалентной строки палиндрома, зная количество вставок, которые должны быть сделаны?

например :

1) azbzczdzez

количество требуемых вставок: 5 Строка палиндрома: azbzcezdzeczbza

хотя несколько строк палиндрома могут существовать для одной строки, но я хочу найти только один палиндром?

10
algorithm dynamic-programming lcs palindrome

5 ответов

пусть S[i, j] представляет подстроку string S начиная с index i и заканчивается на Index j (включительно) и c[i, j] быть оптимальным решением для S[i, j].

очевидно, c[i, j] = 0 if i >= j.

в общем, у нас есть повторения:

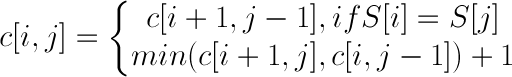
enter image description here

12

чтобы разработать ответ на VenomFangs, есть простое решение для динамического программирования. Обратите внимание, что я предполагаю, что единственная операция, разрешенная здесь, - это вставка символов (без удаления, обновлений). Пусть S-строка из n символов. Простая функция рекурсии P для этого:

    = P [i+1 .. j-1], if S[i] = S[j]

P[i..j] 

    = min (P[i..j-1], P[i+1..j]) + 1,

Если вы хотите больше объяснений, почему это так, опубликуйте комментарий, и я буду рад объяснить (хотя его довольно легко увидеть с небольшим мысль.) Это, кстати, полная противоположность функции LCS, которую вы используете, следовательно, подтверждает, что ваше решение на самом деле оптимально. Конечно, вполне возможно, что я ошибся, если это так, кто-нибудь дайте мне знать!

Edit: для учета самого палиндрома это можно легко сделать следующим образом: Как указано выше, P[1..n] даст вам количество вставок, необходимых для того, чтобы сделать эту строку палиндромом. Как только вышеописанный двумерный массив будет построен, вот как вы найти палиндром:

начните с i=1, j=n. Сейчас, string output ="";

while(i < j)
{
    if (P[i][j] == P[i+1][j-1]) //this happens if no insertions were made at this point
    {
        output = output + S[i];
        i++;
        j--;
    }
    else
    if (P[i][j] == P[i+1][j]) //
    {
        output = output + S[i];
        i++;
    }
    else
    {
        output = S[j] + output;
        j--;
    }
 }
 cout<<output<<reverse(output);
 //You may have to be careful about odd sized palindromes here,
 // I haven't accounted for that, it just needs one simple check

что лучше читать?

2

решение выглядит как решение для динамического программирования.

вы можете найти свой ответ в следующем сообщении:как я могу вычислить количество символов, необходимых для превращения строки в палиндром?

0

PHP решение O (n)

function insertNode(&$arr, $idx, $val) {
    $arr = array_merge(array_slice($arr, 0, $idx), array($val), array_slice($arr, $idx));
}
function createPalindrome($arr, $s, $e) {
    $i = 0;
    while(true) {
        if($s >= $e) {
            break;
        } else if($arr[$s] == $arr[$e]) {
            $s++; $e--; // shrink the queue from both sides 
            continue;
        } else {
            insertNode($arr, $s, $arr[$e]);
            $s++;
        }
    }
    echo implode("", $arr);
}
$arr = array('b', 'e', 'a', 'a', 'c', 'd', 'a', 'r', 'e');
echo createPalindrome ( $arr, 0, count ( $arr ) - 1 );
-1

простой. См. ниже :)

        String pattern = "abcdefghgf";
        boolean isPalindrome = false;
        int i=0,j=pattern.length()-1;
        int mismatchCounter = 0;

        while(i<=j)
        {
            //reverse matching
            if(pattern.charAt(i)== pattern.charAt(j))
                {
                    i++; j--; 
                    isPalindrome = true;
                    continue;
                }

            else if(pattern.charAt(i)!= pattern.charAt(j))
                {
                    i++;
                    mismatchCounter++;
                }


        }
        System.out.println("The pattern string is :"+pattern);
        System.out.println("Minimum number of characters required to make this string a palidnrome : "+mismatchCounter);
-2