Простой способ вычисления точки пересечения двух полигонов в C#
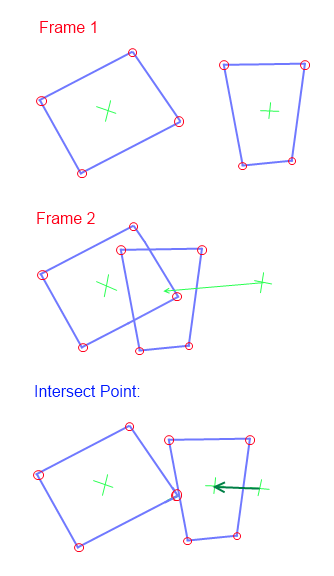
У меня есть два полигона, определенные как список векторов, мне удалось написать подпрограммы для преобразования и пересечения этих двух полигонов (см. ниже Кадр 1). Используя пересечение линий, я могу выяснить, сталкиваются ли они, и написал рабочую функцию Collide ().
Это должно использоваться в игре с переменным шагом, и поэтому (как показано ниже) в кадре 1 правый многоугольник не сталкивается, это совершенно нормально для кадра 2, чтобы многоугольники были прямо внутри каждого другой, с правым многоугольником, переместившимся влево.
мой вопрос в том, каков наилучший способ выяснить момент пересечения? В примере Предположим, что в кадре 1 правый многоугольник находится на X = 300, Кадр 2 переместился на -100 и теперь находится на 200, и это все, что я знаю, к моменту появления кадра 2, он был на 300, теперь он на 200. Я хочу знать, когда он действительно столкнулся, при каком значении X, здесь, вероятно, речь шла 250.
Я предпочтительно ищу решение этой проблемы с исходным кодом на C#. Может быть, есть лучший способ подойти к этому для игр?
5 ответов
Я бы использовал теорему о разделяющей оси, как описано здесь:
тогда я бы развертки тест или использовать multisampling при необходимости.
GMan здесь, в StackOverflow, написал пример реализации на gpwiki.org.
Это может быть излишним для вашего варианта использования, но он обрабатывает полигоны любого порядка. Из конечно, для простых ограничителей это можно сделать гораздо эффективнее с помощью других средств.
Я тоже не математик, но одним из возможных, хотя и грубых решений было бы запустить мини-симуляцию.
назовем движущийся многоугольник M и стационарного полигона S (хотя нет никаких требований для S чтобы на самом деле быть стационарным, подход должен работать одинаково независимо). Давайте также назовем два фрейма, которые у вас есть F1 в начале и F2 для позже в диаграмма.
Если бы вы переводили polygon M вернуться к своей позиции в F1 очень маленькими шагами до тех пор, пока они больше не пересекаются, тогда у вас будет местоположение для M при котором он "просто" пересекается, т. е. предыдущее местоположение, прежде чем они перестанут пересекаться в этой симуляции. Пересечение в этом "просто" пересекающемся месте должно быть очень маленьким - достаточно маленьким, чтобы вы могли рассматривать его как точку. Позволь нам назовите этот многоугольник пересечения Я.
для лечения Я в качестве точки вы можете выбрать ее вершину, ближайшую к центральной точке M на F1: эта вершина имеет наилучшие шансы оказаться вне S в момент столкновения. (Есть много других возможностей для толкования Я как точка, с которой вы могли бы экспериментировать, что может иметь лучшие результаты.)
очевидно, что это подход имеет некоторые недостатки:
- моделирование будет медленнее для больших скоростей M расстояние между его расположения в F1 и F2 будет больше, больше шагов моделирования необходимо будет запустить. (Вы можете решить эту проблему, имея фиксированное количество циклов моделирования независимо от скорости M но это означало бы, что точность результата будет отличаться для более быстрого и медленного перемещения тела.)
- размер "шага" в симуляции должен быть достаточно мал, чтобы получить требуемую точность, но меньшие размеры шага, очевидно, будут иметь большую стоимость расчета.
лично, без необходимой математической интуиции, я бы сначала пошел с этим простым подходом и попытался найти математическое решение в качестве оптимизации позже.
Если у вас есть возможность определить, перекрываются ли два полигона, одной из идей может быть использование модифицированного двоичного поиска для определения того, где два попали. Начните с разделения временного интервала пополам и посмотрите, пересеклись ли два полигона в средней точке. Если это так, рекурсивно найдите первую половину диапазона; если нет, найдите вторую половину. Если вы укажете некоторый уровень допуска, на котором вас больше не волнуют небольшие расстояния (например, на уровне пикселя), то время выполнения этого подхода-O (log D / K), где D-расстояние между полигонами, а K-порог отсечения. Если вы знаете, какая точка в конечном итоге войдет во второй многоугольник, вы сможете очень быстро обнаружить столкновение.
надеюсь, что это помогает!
для довольно общего решения и предполагая ...
- полигоны не пересекаются в момент времени = 0
- по крайней мере один многоугольник пересекает другой многоугольник в момент времени = t
- и вы счастливы использовать библиотеку отсечения C# (например,стрижки)
затем используйте двоичный подход для получения времени пересечения...
double tInterval = t;
double tCurrent = 0;
int direction = +1;
while (tInterval > MinInterval)
{
tInterval = tInterval/2;
tCurrent += (tInterval * direction);
MovePolygons(tCurrent);
if (PolygonsIntersect)
direction = +1;
else
direction = -1;
}
Ну - вы можете видеть, что это всегда точка одного из полигонов, которая сначала попадает в сторону другого (или в другую точку - но это ведь почти одно и то же) - возможным решением было бы вычислить расстояние точек от других линий в направлении движения. Но я думаю, что это закончится довольно медленно.
Я думаю, что обычно расстояния между кадрами настолько малы, что это не важно, чтобы действительно знать, где он ударил первым-некоторые небольшие перекрестки не будут видны, и все равно вещи будут отскакивать или взрываться - не так ли? :)
