проверьте, если четыре точки лежат на одной плоскости, только с помощью расстояния (проверить colinearity)

существует метод под названием Кэли-Менгера чтобы найти, если 3 точки коллинеарны, 4 точки являются копланарными и т. д. при условии, что заданы все попарные расстояния.

однако в 2-D есть очень простой способ определить, являются ли 3 точки, {A,B, C} коллинеарными: неравенство треугольника!

!(|AB| + |AC| = |BC|) и !(|AB| + |BC| = |AC|) и !(|AC| + |BC| = |AB|) IFF A, B, C не коллинеар

есть ли аналогичный подход в 3-D?

7
algorithm c++ geometry linear-algebra math

1 ответов

Да, существует аналогичная формула для трех измерений.

Решение 1

четыре точки находятся в одной плоскости, если и только если одна из областей четырех треугольников, которые вы можете сделать, имеет площадь, равную сумме (или сумме / разности, например, P1=P2+P3-P4) другие три области.

Heron формула гласит, что площадь A треугольника с вершинами a, b, c и

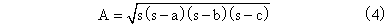
enter image description here

здесь s = 0.5 (a + b + c). Таким образом, вы можете вычислить каждую область с ваших расстояний и проверить, выполняется ли условие.

решение 2

четыре точки находятся в одной плоскости тогда и только тогда, когда объем тетраэдра, состоящего из этих четырех точек, равен 0.

формула цапли дает объем тетраэдра в терминах его ребер, таким образом, вы можете проверить это, основываясь только на расстояниях. Вот краткий вывод формулы.

треугольное равенство можно увидеть только в частном случае Герона формула для вычисления содержания n - мерного симплекса из это n + 1 вершин. Содержание a n-мерный симплекс 1 / n! умножает "высоты" вершин (взятых в любой линейной последовательности) над подпространством, содержащим предыдущие вершины. Представьте себе, как вы умножаете базис треугольника на его высоту ( и с 1/2), чтобы получить область треугольника, затем умножьте эту область на высоту (и 1/3) тетраэдра, чтобы получить его объем, и так далее.

заметим, что любая вершина симплекса в k-мерном пространстве можно рассматривать как вершину "пирамиды" на (к-1)-размерная база, определяемая другими вершинами. Пусть ВК-1 обозначим содержание базы, и h перпендикулярное расстояние вершины от подпространства, содержащего основание, содержание Vk пирамиды дают

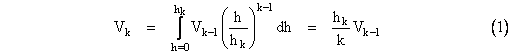
enter image description here

поэтому, применяя эту формулу к вершинам (в любом порядке) рекурсивно, начиная с k = n, мы

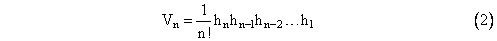
enter image description here

здесь h1 - это просто расстояние между двумя вершинами, h2 - высота третьей вершины над линией, содержащей эти две вершины,h3 - высота четвертой вершины над плоскостью, содержащей первые три вершины и так далее. Таким образом, содержание n-мерный симплекс 1 / n! умножает "высоты" вершин (взятых в любой линейной последовательности) над подпространством, содержащим предыдущие вершины.

вообще мы можем приложить n-размерное вращение, которое помещает n-1 вершин в подпространство, ортогональное одной из осей.

это приводит нас к Кэли-Менгера, для площади треугольника в терминах длин ребер

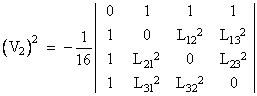
enter image description here

дает Герона формула для площади треугольника в терминах длин ребер

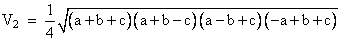
enter image description here

формула цапли для Тома тетраэдра

если U, V, W, u, v, w - длины ребер тетраэдра (первые три образуют треугольник; u напротив U и так далее), то

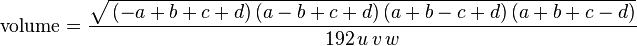
enter image description here

где:

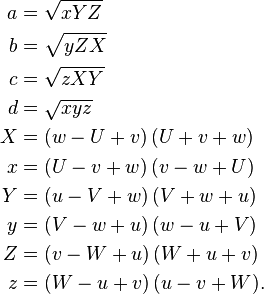
enter image description here

если одна из точек расположена на плоскости, определяемой тремя другими точками, объем равен 0, поэтому одна из факторов в числителе 0 и это условие можно проверить.

Формула цапли и обобщение Брахмагупты

Тетраэдр

Я написал функцию heron_3d на C++. Эта функция возвращает boolean значение, указывающее, принадлежат ли 4 точки одной плоскости или нет, Используя подход, описанный в Решение 1: сравнение каждой грани тетраэдра с суммой из 3 других лиц, использующих Герона формула для расчета каждой области.

#include <cmath>
/**
 * @return area of triangle based on Heron formula
 */
double areaOfTriangle( double edge1, double edge2, double edge3) {
    double s = 0.5 * ( edge1 + edge2 + edge3);
    return std::sqrt( s * ( s - edge1) * ( s - edge2) * ( s - edge3));
}
/**
 * U, V, W, u, v, w are lengths of edges of the tetrahedron, as in 
 * http://en.wikipedia.org/wiki/Tetrahedron
 * @param U basis edge 1
 * @param V basis edge 2
 * @param W basis edge 3
 * @param u opposite to U
 * @param v opposite to V
 * @param w opposite to W
 * @return 
 */
bool heron_3d( double U, double V, double W,
               double u, double v, double w) {
    double areas[] = { areaOfTriangle( U, V, W),
                       areaOfTriangle( U, v, w),
                       areaOfTriangle( V, u, w),
                       areaOfTriangle( W, u, v)};
    for ( int i = 0; i < 4; ++i) {
        double area = areas[ i];
        double sum = 0;
        for ( int j = 1; j < 4; ++j) {
            sum += areas[ (i + j) % 4];
        }
        if ( area == sum) return true;
    }
    return false;
}

использование:

int main(int argc, char** argv) {

    bool b0 = heron_3d( 3, 3, 0, 5, 5, 4);  // true
    bool b1 = heron_3d( 3, 3.1, 0.1, 5.1, 5, 4); // false
    bool b2 = heron_3d( 3, 5, 2, std::sqrt( 16 + 25), 5, 4); // true
    return 0;
}
9