Проверьте, подходят ли три круга внутри треугольника

Я думал некоторое время о написании программы, которая говорит мне, могут ли три круга с заданными диаметрами поместиться внутри треугольника с заданной длиной стороны без перекрытия (прикосновение нормально) друг друга.

Как можно подумать об этом?

10
geometry math

4 ответов

Я бы попытался найти способ перечислить возможные конфигурации для трех кругов, а затем протестировать каждую конфигурацию, пока не будет найдено, где подходят три круга, или пока все конфигурации не будут протестированы и отклонены.

(в дальнейшем я предполагаю, что каждый круг, как известно, вписывается в треугольник сам по себе. Очевидно, что если какой-либо круг не подходит сам по себе, то он не вписывается в любую конфигурацию из трех кругов.)

конфигурация (1) включает в себя размещение круга в каждом углу треугольника. (Это конфигурация, которую все заметили.)

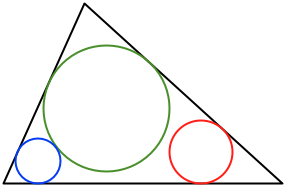
a triangle with a big green circle in the top corner, a medium red circle in the bottom right corner, and a small blue circle in the bottom left corner

существует шесть способов расположить круги, и для каждого расположения достаточно проверить, будут ли круги соответствовать попарно:

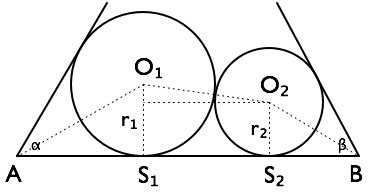
circle with centre O₁ and radius r₁ in the bottom left corner of a triangle (marked A with angle α) and circle with centre O₂ and radius r₂ in the bottom right (marked B with angle β)

расстояние AS₁ является r₁/Тан(½α), расстояние S₂B является r₂/Тан(½β), а расстояние S₁S₂ в √((r₁ + r₂)2 - (r₁ - r₂)2) = 2√r₁r₂

круги подходят, если AS₁ + S ≤S ≤ + S ≤B ≤ AB.

в конфигурации (2) мы помещаем два круга в два угла треугольника, а третий круг между этими двумя и одним из двух краев, которые не касаются обоих кругов:

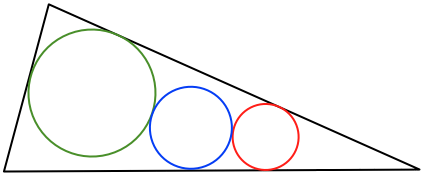
a thin triangle with a big green circle in the top left corner, a medium red circle in the right corner, and a blue circle between them and the top edge

выяснить, будут ли они соответствовать немного сложнее:

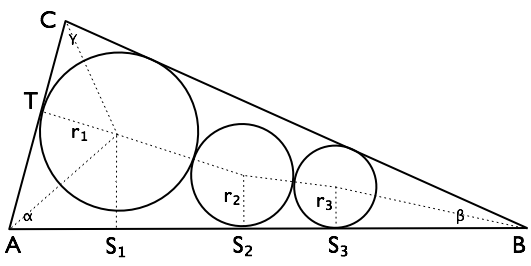
the thin triangle marked up: T is where the altitude from centre of the big circle meets the left edge, and S₁ to S₃ are where altitudes from the centres of the three circles meet the bottom edge

чтобы найти длину КАК₁ мы должны обойти треугольник от угла C через точку T. я оставлю детали этого в качестве упражнения.

есть восемнадцать способов расположить круги в этой конфигурации.

есть ли конфигурация (3)? Я посмотрел, но не смог найти ни одного, который не мог бы быть превращен в один из двух, которые я дал. Например, если все три круга касаются одной и той же стороны, всегда есть место для замены среднего круга на противоположную сторону, получая конфигурацию (2). Однако перечисление геометрических конфигураций всегда сложно, и я мог бы легко иметь пропустил одну.

4

просто предположение: ваша проблема может быть связана с кругами Апполония.

Я столкнулся с ним, пытаясь рекурсивно вписать 3 круга в 4-й без пересечения для некоторой фрактальной анимации, поэтому, возможно, стоит попробовать.

вы найдете это подробно объяснено в Wolfram (эта проблема была решена только в 1968 году): http://mathworld.wolfram.com/ApolloniusProblem.html

1

Это, кажется, сложная и интересная проблема. Через решение мраморной проблемы (связанной с круги Малфатти) Лос и Залгаллер в 1994 году, это может быть возможным для вас, чтобы нудно извлечь необходимые условие существования конфигурации из трех непересекающихся окружностей с заданными радиусами внутри треугольника с заданными длинами сторон. Если вы можете разместить их внутри треугольника, сумма их площадей будет не более максимальной площадь трех треугольников внутри круга. Мраморная задача-задача определения максимальной площади трех неперекрывающихся окружностей внутри данного треугольника. Прямо сейчас, я не вижу, что это тоже достаточно.

возможно, для начала стоило бы ввести ε в задачу, а затем искать алгоритм, который в конечном числе шагов мог бы определить, является ли конфигурация, которая не более "плохой ε" (определенная каким-то разумным образом) существует.

некоторые из лучших математиков мира регулярно участвуют в сестре stackoverflow, mathoverflow.org, поэтому вы можете попробовать опубликовать эту проблему там.

Спасибо за размещение этого.

0

Я думаю, что достаточно попробовать все 6 возможных перестановок (A1 B2 C3, A2 B1 C3, A1 B3 C2, A3 B1 C2, A2 B3 C1, A3 B2 C1). Если круг не касателен к двум краям треугольника, то его размещение в некотором смысле неоптимально, и вы можете сделать больше места для двух других, сдвинув его в угол. Если можно вставить три круга в треугольник без их перекрытия, то, вероятно, можно сдвинуть их в углы (для случая, когда они все застряли против краев поднимите их все вместе и поверните на 60 градусов). Конечно, это не строгое доказательство, но я уверен, что это работает. Кроме того, я полагаю, что решение всегда будет заключаться в размещении самых больших кругов под самыми широкими углами, потому что именно они потенциально могут занимать самое центральное пространство треугольника.

0