python-как получить высокую и низкую огибающую сигнала?

есть ли аналогичная функция в Python, которая может это сделать?

насколько мне известно, в Numpy / Scipy / Python нет такой функции. Однако создать его не так уж трудно. Общая идея такова:--7-->

заданный вектор значений:

1. найти местоположение пиков (ов). Назовем их (u)
2. найти расположение желобов s. Назовем их (l).
3. установить модель на (у) пары значений. Назовем это (u_p)
4. установите модель в пары значений (l). Назовем это (l_p)
5. Evaluate (u_p) над доменом (s), чтобы получить интерполированные значения верхнего конверта. (Назовем их (q_u))
6. Evaluate (l_p) над доменом (s), чтобы получить интерполированные значения Нижнего конверта. (Давайте назовем их (q_l)).

как вы можете видеть, это последовательность из трех шагов (найти местоположение, модель fit, оценить модель), но применяется дважды, один раз для верхней части конверта и один для нижней.

чтобы собрать" пики "(ов), вам нужно найти точки, где наклон (ов) изменяется от положительного к отрицательному, и собрать" впадины " (ов), вам нужно найти точки, где наклон (ов) изменяется от отрицательного к положительному.

пиковый пример: s = [4,5,4] 5-4 положительный 4-5 отрицательный

пример корыта: s = [5,4,5] 4-5 отрицательно 5-4 положительно

вот пример скрипта, чтобы вы начали с большим количеством встроенных комментариев:

from numpy import array, sign, zeros
from scipy.interpolate import interp1d
from matplotlib.pyplot import plot,show,hold,grid

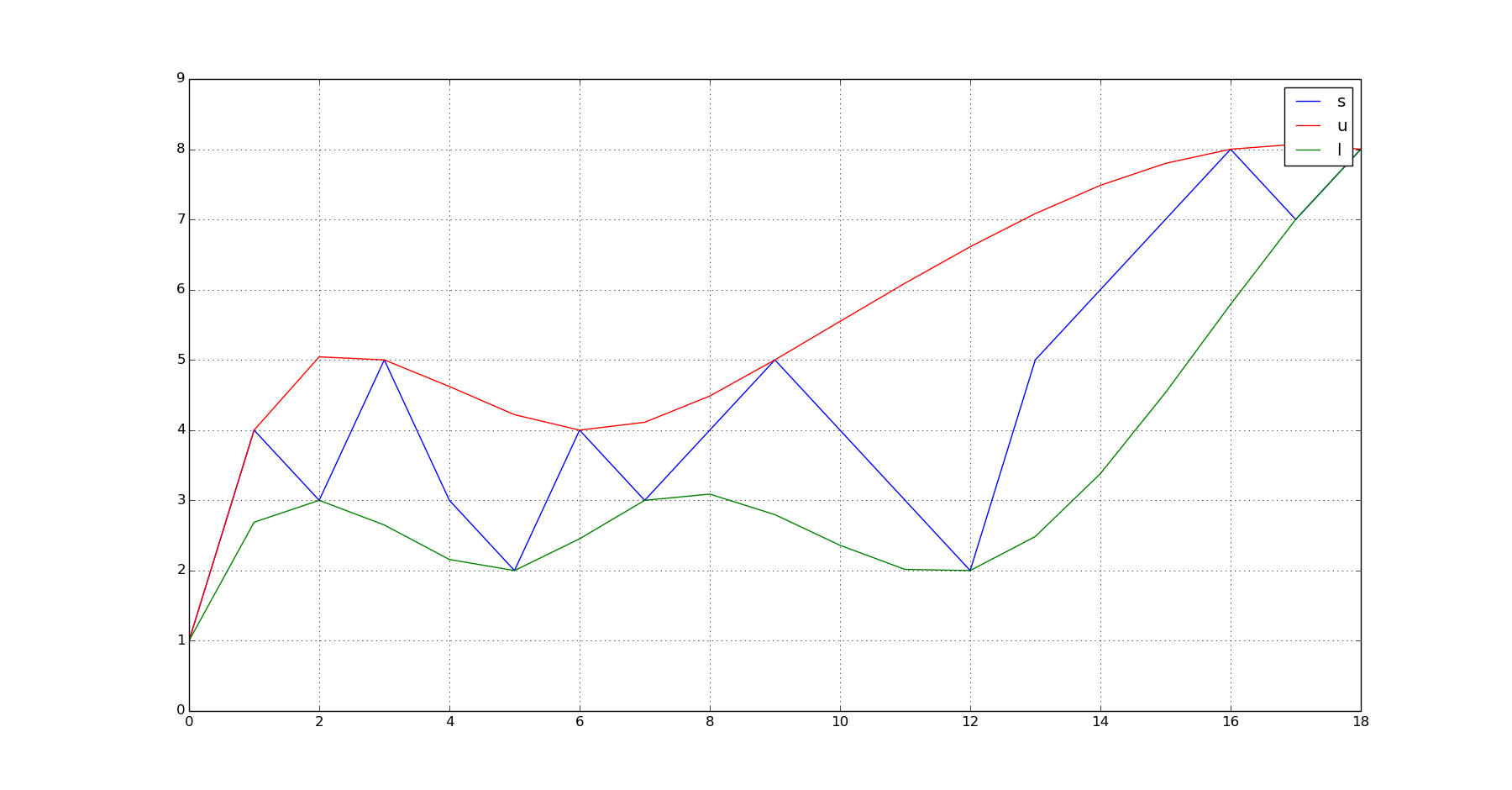
s = array([1,4,3,5,3,2,4,3,4,5,4,3,2,5,6,7,8,7,8]) #This is your noisy vector of values.

q_u = zeros(s.shape)
q_l = zeros(s.shape)

#Prepend the first value of (s) to the interpolating values. This forces the model to use the same starting point for both the upper and lower envelope models.

u_x = [0,]
u_y = [s[0],]

l_x = [0,]
l_y = [s[0],]

#Detect peaks and troughs and mark their location in u_x,u_y,l_x,l_y respectively.

for k in xrange(1,len(s)-1):
    if (sign(s[k]-s[k-1])==1) and (sign(s[k]-s[k+1])==1):
        u_x.append(k)
        u_y.append(s[k])

    if (sign(s[k]-s[k-1])==-1) and ((sign(s[k]-s[k+1]))==-1):
        l_x.append(k)
        l_y.append(s[k])

#Append the last value of (s) to the interpolating values. This forces the model to use the same ending point for both the upper and lower envelope models.

u_x.append(len(s)-1)
u_y.append(s[-1])

l_x.append(len(s)-1)
l_y.append(s[-1])

#Fit suitable models to the data. Here I am using cubic splines, similarly to the MATLAB example given in the question.

u_p = interp1d(u_x,u_y, kind = 'cubic',bounds_error = False, fill_value=0.0)
l_p = interp1d(l_x,l_y,kind = 'cubic',bounds_error = False, fill_value=0.0)

#Evaluate each model over the domain of (s)
for k in xrange(0,len(s)):
    q_u[k] = u_p(k)
    q_l[k] = l_p(k)

#Plot everything
plot(s);hold(True);plot(q_u,'r');plot(q_l,'g');grid(True);show()

это производит этот выход:

очки для дальнейшего улучшения:

1. приведенный выше код не фильтр пики или впадины, которые могут происходить ближе, чем некоторое пороговое "расстояние" (Tl) (например, время). Это похоже на второй параметр envelope. Это легко добавьте его, Хотя, изучив различия между последовательными значениями u_x,u_y.

2. тем не менее, быстрое улучшение по сравнению с пунктом, упомянутым ранее, - это фильтр нижних частот с фильтром скользящей средней до интерполяция функций верхнего и нижнего огибающих. Вы можете сделать это легко, свернув ваш (ы) с подходящим фильтром скользящей средней. Не вдаваясь в подробности здесь (можно сделать при необходимости), для получения фильтра скользящей средней это работает над N последовательными образцами, вы бы сделали что-то вроде этого: s_filtered = numpy.convolve(s, numpy.ones((1,N))/float(N). Чем выше (N), тем более плавными будут отображаться ваши данные. Обратите внимание, однако, что это сдвинет ваши (ы) значения (N/2) выборки вправо (в s_filtered) из-за того, что называется групповая задержка сглаживающего фильтра. Дополнительные сведения о скользящей средней см. В разделе этой ссылке.

надеюсь, что это помогает.

(рад ammend ответ, если предоставлена дополнительная информация об исходном приложении. Возможно, данные могут быть предварительно обработаны более подходящим способом (?))