Python & Pygame: столкновение шара с внутренней частью круга
Я делаю игру в которой шары отказов вокруг внутри большой круг. Большой круг не двигается.
вот код, который я в настоящее время использую для этих столкновениях:
def collideCircle(circle, ball):
"""Check for collision between a ball and a circle"""
dx = circle.x - ball.x
dy = circle.y - ball.y
distance = math.hypot(dx, dy)
if distance >= circle.size + ball.size:
# We don't need to change anything about the circle, just the ball
tangent = math.atan2(dy, dx)
ball.angle = 2 * tangent - ball.angle
ball.speed *= elasticity + 0.251
angle = 0.5 * math.pi + tangent
ball.x -= math.sin(angle)
ball.y += math.cos(angle)
Он основан на замечательном учебнике исполнителя Peter Collingridge здесь.
объекты круга и шара являются обоими классами, с (x,y), радиусом, углом и скоростью.
у меня две проблемы с этим методом, однако:
- мяч отскакивает от (что я подозреваю) - это его "Якорная точка", которая, кажется, находится в правом верхнем углу круга.
- при столкновении с нижним 5% круга, не удается отскочить достаточно высоко и, следовательно, "тонет" из экрана. Я предполагаю, что это потому, что отскок недостаточно высок, чтобы переместить мяч выше его (неправильно размещенной) "точки привязки"?
рассмотрев возможные решения уже на здесь, в частности," быстрое обнаружение столкновений круга " [ссылка удалена из-за ограничения спам-ссылки], который, хотя в Java используется тот же метод, все они имеют дело с внешними столкновениями, в то время как я смотрю на подпрыгивание шара вокруг внутренней части круга.
вот также определения классов шара() и круга():
class Ball():
def __init__(self, (x,y), size):
"""Setting up the new instance"""
self.x = x
self.y = y
self.size = size
self.colour = (0,128,255)
self.thickness = 0
self.speed = 0.01
self.angle = math.pi/2
def display(self):
"""Draw the ball"""
pygame.draw.circle(screen, self.colour, (int(self.x), int(self.y)), self.size, self.thickness)
def move(self):
"""Move the ball according to angle and speed"""
self.x += math.sin(self.angle) * self.speed
self.y -= math.cos(self.angle) * self.speed
(self.angle, self.speed) = addVectors((self.angle, self.speed), gravity)
self.speed *= drag
class Circle():
def __init__(self, (x,y), size):
"""Set up the new instance of the Circle class"""
self.x = x
self.y = y
self.size = size
self.colour = (236, 236, 236)
self.thickness = 0
self.angle = 0 # Needed for collision...
self.speed = 0 # detection against balls
def display(self):
"""Draw the circle"""
pygame.draw.circle(screen, self.colour, (int(self.x), int(self.y)), self.size, self.thickness
заранее спасибо, Натан
3 ответов
Я рада, что вам понравился мой учебник. Мне нравится ваша вариация, она должна быть проще.
во-первых, я думаю, вам нужно изменить тест для столкновения:
if distance >= circle.size - ball.size:
потому что чем больше размер шара, тем меньше расстояние между его центром и центром круга может быть. Это должно заставить шары отскакивать в нужном месте (внутри круга).
тогда я думаю, что вам просто нужно поменять знаки на x и y, и все должно работа.
ball.x += math.sin(angle)
ball.y -= math.cos(angle)
чтобы переместить мяч на правильное расстояние, вы можете рассчитать перекрытие:
overlap = math.hypot(dx, dy) - (circle.size - ball.size)
if overlap >= 0:
tangent = math.atan2(dy, dx)
ball.angle = 2 * tangent - ball.angle
ball.speed *= elasticity
angle = 0.5 * math.pi + tangent
ball.x += math.sin(angle)*overlap
ball.y -= math.cos(angle)*overlap
удачи
не отвечая на ваш вопрос, я хотел бы прокомментировать вашу стратегию реализации и рекомендовать новый подход. Вы представляете скорость шара в полярной координатной форме, как ball.angle и ball.speed.
Я думаю, что это будет вообще неудобно. Например, в вашем коде столкновения вы в конечном итоге вызываете atan2 повернуть вектор (dx, dy) в угол, а затем вы называете sin и cos чтобы повернуть угол назад в вектор снова. (Кроме того, если вы когда-нибудь попытаетесь обобщить свой код на три измерения, вы окажетесь в мире боли.) Итак, если у вас нет особых требований, требующих полярных координат, я рекомендую вам делать то, что делают все остальные, а именно представлять скорость шара в декартовых координатах как вектор (vx, vy).
Я также рекомендую изменить свой подход к физике с статический one ("объект A в настоящее время сталкивается с объект Б?") к динамический one ("будет ли объект A сталкиваться с объектом B во время следующего шага движения?"). В статической физической системе вы часто заканчиваете тем, что объекты пересекаются друг с другом в конце шага движения, а затем вам нужно выяснить лучший способ заставить их снова разделиться, что трудно получить правильно.
если вы делаете оба из них, это просто, чтобы отскочить мяч без какой-либо тригонометрии.
Шаг 1. Transform circle/круг столкновение в точку / круг столкновения с помощью Минковского дополнение:

Шаг 2. Рассмотрим отрезок времени, в котором мяч начинается с p = (px, py) и движется по v = (vx,vy). Пересекается ли она с кругом? Вы можете использовать стандартный сегмент линии / тест круга для этого за исключением того, что смысл теста обращен вспять.
Шаг 3. Найти точку столкновения c = (cx, cy). Мяч отскакивает от круга так же, как он отскакивает от линии t касательной к окружности в этой точке. Для круга, центрированного в начале координат, касательный вектор просто (- cy, cx), и я уверен, что вы можете вычислить его для других кругов.
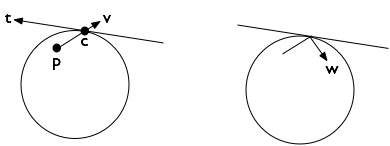
посмотреть этот ответ для того, чтобы рассчитать новую траекторию шара на основе коэффициентов трения и восстановления.
Шаг 4. Не забудьте, что мяч все еще может иметь некоторое расстояние для перемещения по новому вектору w. Если временной шаг достаточно велик или скорость достаточно высока, он может столкнуться снова в течение того же отрезка времени.
большинство графических пакетов используют верхний левый в качестве начала для рисования кода. Скорее всего, вы хотите 2 набора координат, с которыми вы сталкиваетесь/перемещаетесь/и т. д., а один для рисования (X-радиус, y-радиус).
кроме того, не думая об этом слишком много, если проверка пересечения будет distance + ball.size >= circle.size? Расстояние шарика от центра, плюс ее радиус должен быть меньше радиуса круга, если я правильно понял настройки.
