quicksort в худшем случае условие
когда алгоритм quicksort принимает время O (n^2)?
6 ответов
Quicksort работает, беря ось, затем помещая все элементы ниже этой оси с одной стороны и все более высокие элементы с другой; затем рекурсивно сортирует две подгруппы таким же образом (до тех пор, пока все не будет отсортировано.) Теперь, если вы каждый раз выбираете худший pivot (самый высокий или самый низкий элемент в списке), у вас будет только одна группа для сортировки, со всем в этой группе, кроме исходного pivot, который вы выбрали. Это по сути дает вам n групп, которые каждый должен быть повторен через n раз, следовательно, сложность O(n^2).
наиболее распространенной причиной этого является выбор pivot в качестве первого или последнего элемента в списке в реализации quicksort. Для несортированных списков это так же верно, как и любое другое, однако для отсортированных или почти отсортированных списков (которые встречаются довольно часто на практике) это, скорее всего, даст вам худший сценарий. Вот почему все наполовину приличные реализации, как правило, принимают поворот от в центре списка.
существуют модификации стандартного алгоритма quicksort, чтобы избежать этого крайнего случая - одним из примеров является двойной поворот quicksort, который был интегрирован в Java 7.
получение пивота, равного наименьшему или наибольшему числу, также должно вызвать наихудший сценарий O (n2).
короче Quicksort для сортировки массива самый низкий элемент сначала работает следующим образом:
- выберите элемент pivot
- массив Presort, такой, что все элементы меньше, чем ось, находятся на левой стороне
- рекурсивно выполните шаг 1. и 2. для левой стороны и правой стороны
обычно вы бы сводный элемент, который разбивает последовательность на две одинаково длинные подпоследовательности.
теперь есть разные схемы выбора элемента pivot. ранняя версия просто взял самый левый элемент. В худшем случае, однако, элемент pivot всегда будет w.l.o.г. низший элемент.
крайний левый элемент-pivot
в этом случае можно легко придумать, что худшим случаем является уже увеличивающийся отсортированный массив:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
самый правый элемент-pivot
аналогично при выборе самого правого элемента в худшем случае будет быть убывающей последовательностью.
20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
центральным элементом является pivot
одним из возможных решений является использование центрального элемента (или немного слева от центра, если последовательность имеет четную длину). В этом случае худший вариант был бы более экзотичным. Он может быть построен путем изменения алгоритма Quicksort для установки элементов массива, соответствующих выбранному в данный момент элементу pivot, на монотонное возрастающее значение. Т. е. мы знаем, что первая ось-это центр, поэтому центр должно быть наименьшее значение, например 0. Затем он заменяется на самый левый, т. е. самое левое значение теперь находится в центре и будет следующим элементом поворота, поэтому оно должно быть 1, поэтому мы уже догадываемся, что массив будет выглядеть так:
1 ? ? 0 ? ? ?
мы можем позволить модифицированной Quicksort сделать все остальное. Вот код на C++:
// g++ -std=c++11 worstCaseQuicksort.cpp && ./a.out
#include <algorithm> // swap
#include <iostream>
#include <vector>
#include <numeric> // iota
int main( void )
{
std::vector<int> v(20); /**< will hold the worst case later */
/* p basically saves the indices of what was the initial position of the
* elements of v. As they get swapped around by Quicksort p becomes a
* permutation */
auto p = v;
std::iota( p.begin(), p.end(), 0 );
/* in the worst case we need to work on v.size( sequences, because
* the initial sequence is always split after the first element */
for ( auto i = 0u; i < v.size(); ++i )
{
/* i can be interpreted as:
* - subsequence starting index
* - current minimum value, if we start at 0 */
/* note thate in the last step iPivot == v.size()-1 */
auto const iPivot = ( v.size()-1 + i )/2;
v[ p[ iPivot ] ] = i;
std::swap( p[ iPivot ], p[i] );
}
for ( auto x : v ) std::cout << " " << x;
}
мы получаем эти наихудшие последовательности:
0
0 1
1 0 2
2 0 1 3
1 3 0 2 4
4 2 0 1 3 5
1 5 3 0 2 4 6
4 2 6 0 1 3 5 7
1 5 3 7 0 2 4 6 8
8 2 6 4 0 1 3 5 7 9
1 9 3 7 5 0 2 4 6 8 10
6 2 10 4 8 0 1 3 5 7 9 11
1 7 3 11 5 9 0 2 4 6 8 10 12
10 2 8 4 12 6 0 1 3 5 7 9 11 13
1 11 3 9 5 13 7 0 2 4 6 8 10 12 14
8 2 12 4 10 6 14 0 1 3 5 7 9 11 13 15
1 9 3 13 5 11 7 15 0 2 4 6 8 10 12 14 16
16 2 10 4 14 6 12 8 0 1 3 5 7 9 11 13 15 17
1 17 3 11 5 15 7 13 9 0 2 4 6 8 10 12 14 16 18
10 2 18 4 12 6 16 8 14 0 1 3 5 7 9 11 13 15 17 19
1 11 3 19 5 13 7 17 9 15 0 2 4 6 8 10 12 14 16 18 20
16 2 12 4 20 6 14 8 18 10 0 1 3 5 7 9 11 13 15 17 19 21
1 17 3 13 5 21 7 15 9 19 11 0 2 4 6 8 10 12 14 16 18 20 22
12 2 18 4 14 6 22 8 16 10 20 0 1 3 5 7 9 11 13 15 17 19 21 23
1 13 3 19 5 15 7 23 9 17 11 21 0 2 4 6 8 10 12 14 16 18 20 22 24
в этом есть порядок. Правая сторона-это просто инкременты из двух, начинающиеся с нуль. Левая сторона также имеет порядок. Давайте отформатируем левую сторону для длинной последовательности худшего случая 73 элемента, используя Ascii art:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
------------------------------------------------------------------------------------------------------------
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35
37 39 41 43 45 47 49 51 53
55 57 59 61 63
65 67
69
71
заголовок-это индекс элемента. В первой строке каждому 2-му элементу присваиваются номера, начинающиеся с 1 и увеличивающиеся на 2. Во второй строке то же самое делается с каждым 4-м элементом, в 3-й строке номера присваиваются каждому 8-му элементу и так далее. В этом случае первое значение, записанное в i-й строке, находится в индексе 2^i - 1, но для определенной длины это выглядит немного иначе.
полученная структура напоминает перевернутую двоичное дерево, узлы которого помечены "снизу-вверх", начиная с листьев.
медиана крайних левых, центральных и правых элементов-pivot
другой способ-использовать медиану самого левого, центра и самого правого элемента. В этом случае худшим случаем может быть только то, что w.l.o.г. левая подпоследовательность имеет длину 2 (а не только длину 1, как в примеры выше). Также мы предполагаем, что самое правое значение всегда будет самым высоким из медианы-из-трех. Это также означает, что высшая из всех ценностей. Внося коррективы в программу выше, мы теперь имеем следующее:
auto p = v;
std::iota( p.begin(), p.end(), 0 );
auto i = 0u;
for ( ; i < v.size(); i+=2 )
{
auto const iPivot0 = i;
auto const iPivot1 = ( i + v.size()-1 )/2;
v[ p[ iPivot1 ] ] = i+1;
v[ p[ iPivot0 ] ] = i;
std::swap( p[ iPivot1 ], p[i+1] );
}
if ( v.size() > 0 && i == v.size() )
v[ v.size()-1 ] = i-1;
генерируемые последовательности:
0
0 1
0 1 2
0 1 2 3
0 2 1 3 4
0 2 1 3 4 5
0 4 2 1 3 5 6
0 4 2 1 3 5 6 7
0 4 2 6 1 3 5 7 8
0 4 2 6 1 3 5 7 8 9
0 8 2 6 4 1 3 5 7 9 10
0 8 2 6 4 1 3 5 7 9 10 11
0 6 2 10 4 8 1 3 5 7 9 11 12
0 6 2 10 4 8 1 3 5 7 9 11 12 13
0 10 2 8 4 12 6 1 3 5 7 9 11 13 14
0 10 2 8 4 12 6 1 3 5 7 9 11 13 14 15
0 8 2 12 4 10 6 14 1 3 5 7 9 11 13 15 16
0 8 2 12 4 10 6 14 1 3 5 7 9 11 13 15 16 17
0 16 2 10 4 14 6 12 8 1 3 5 7 9 11 13 15 17 18
0 16 2 10 4 14 6 12 8 1 3 5 7 9 11 13 15 17 18 19
0 10 2 18 4 12 6 16 8 14 1 3 5 7 9 11 13 15 17 19 20
0 10 2 18 4 12 6 16 8 14 1 3 5 7 9 11 13 15 17 19 20 21
0 16 2 12 4 20 6 14 8 18 10 1 3 5 7 9 11 13 15 17 19 21 22
0 16 2 12 4 20 6 14 8 18 10 1 3 5 7 9 11 13 15 17 19 21 22 23
0 12 2 18 4 14 6 22 8 16 10 20 1 3 5 7 9 11 13 15 17 19 21 23 24
псевдослучайный элемент со случайным семенем 0 является pivot
наихудшие последовательности для центрального элемента и медианы-из-трех выглядят уже довольно случайными, но для того, чтобы сделать Quicksort еще более надежный элемент pivot можно выбрать случайным образом. Если используемая случайная последовательность, по крайней мере, воспроизводима при каждом запуске Quicksort, то мы также можем построить последовательность наихудшего случая для этого. Нам нужно только настроить iPivot = в первой программе, например:
srand(0); // you shouldn't use 0 as a seed
for ( auto i = 0u; i < v.size(); ++i )
{
auto const iPivot = i + rand() % ( v.size() - i );
генерируемые последовательности:
0
1 0
1 0 2
2 3 1 0
1 4 2 0 3
5 0 1 2 3 4
6 0 5 4 2 1 3
7 2 4 3 6 1 5 0
4 0 3 6 2 8 7 1 5
2 3 6 0 8 5 9 7 1 4
3 6 2 5 7 4 0 1 8 10 9
8 11 7 6 10 4 9 0 5 2 3 1
0 12 3 10 6 8 11 7 2 4 9 1 5
9 0 8 10 11 3 12 4 6 7 1 2 5 13
2 4 14 5 9 1 12 6 13 8 3 7 10 0 11
3 15 1 13 5 8 9 0 10 4 7 2 6 11 12 14
11 16 8 9 10 4 6 1 3 7 0 12 5 14 2 15 13
6 0 15 7 11 4 5 14 13 17 9 2 10 3 12 16 1 8
8 14 0 12 18 13 3 7 5 17 9 2 4 15 11 10 16 1 6
3 6 16 0 11 4 15 9 13 19 7 2 10 17 12 5 1 8 18 14
6 0 14 9 15 2 8 1 11 7 3 19 18 16 20 17 13 12 10 4 5
14 16 7 9 8 1 3 21 5 4 12 17 10 19 18 15 6 0 11 2 13 20
1 2 22 11 16 9 10 14 12 6 17 0 5 20 4 21 19 8 3 7 18 15 13
22 1 15 18 8 19 13 0 14 23 9 12 10 5 11 21 6 4 17 2 16 7 3 20
2 19 17 6 10 13 11 8 0 16 12 22 4 18 15 20 3 24 21 7 5 14 9 1 23
Итак, как проверить правильность этих последовательностей?
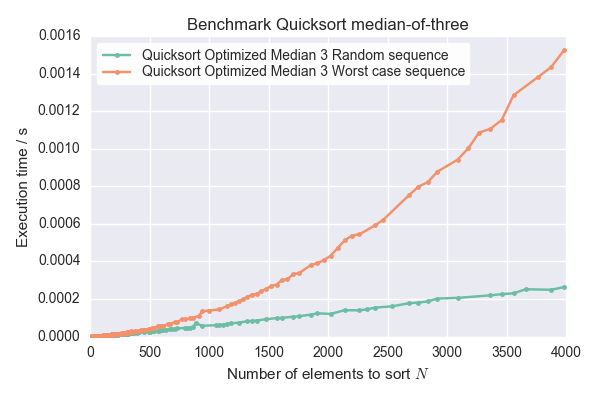
- измерьте время, необходимое для последовательностей. Время участка над длина последовательности N. Если кривая масштабируется с O(N^2) вместо O(N log (N)), то это действительно наихудшие последовательности.
- настройте правильный Quicksort, чтобы дать отладочный вывод о длинах подпоследовательности и / или выбранных элементах поворота. Одна из подпоследовательностей всегда должна иметь длину 1 (или 2 для медианы из трех). Выбранные печатные элементы pivot должны увеличиваться.
различных реализаций быстрой сортировки имеют различные наборы данных, чтобы дать ему время наихудших. Это зависит от того, где алгоритм выбирает его оси элемента.
а также, Как сказал Ghpst, выбор самого большого или самого маленького числа даст вам worstcase.
Если я правильно помню, quicksort обычно использует случайный элемент для pivot, чтобы свести к минимуму вероятность получения worstcase.
Я думаю, что если массив находится в порядке revrse, то это будет худший случай для pivot последнего элемента этого массива
факторы, которые способствуют худшему сценарию quicksort, следующие:
- худший случай возникает, когда в подмассивах полностью несбалансированного
- наихудший случай возникает, когда в одном поддиапазоне есть 0 элементов и
n-1элементы в другом.
другими словами, наихудшее время работы quicksort происходит, когда Quicksort принимает отсортированный массив (в порядке убывания), чтобы быть на временной сложности O (n^2).