R интерполированный полярный контурный график
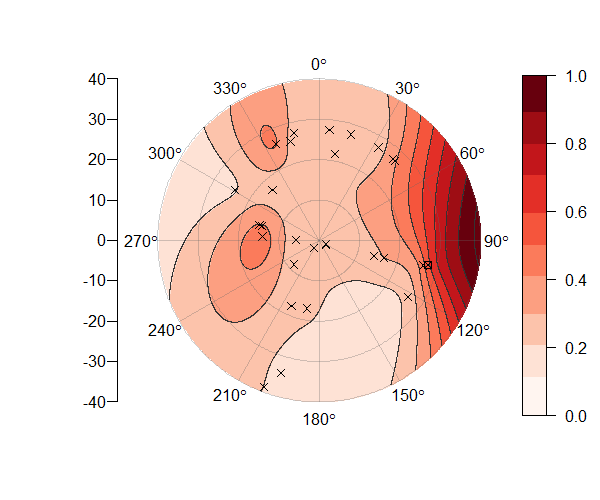
Я пытаюсь написать контурный полярный график в R из интерполированных точечных данных. Другими словами, у меня есть данные в полярных координатах со значением величины, которое я хотел бы построить и показать интерполированные значения. Я хотел бы массово производить участки, похожие на следующие (произведенные в OriginPro):
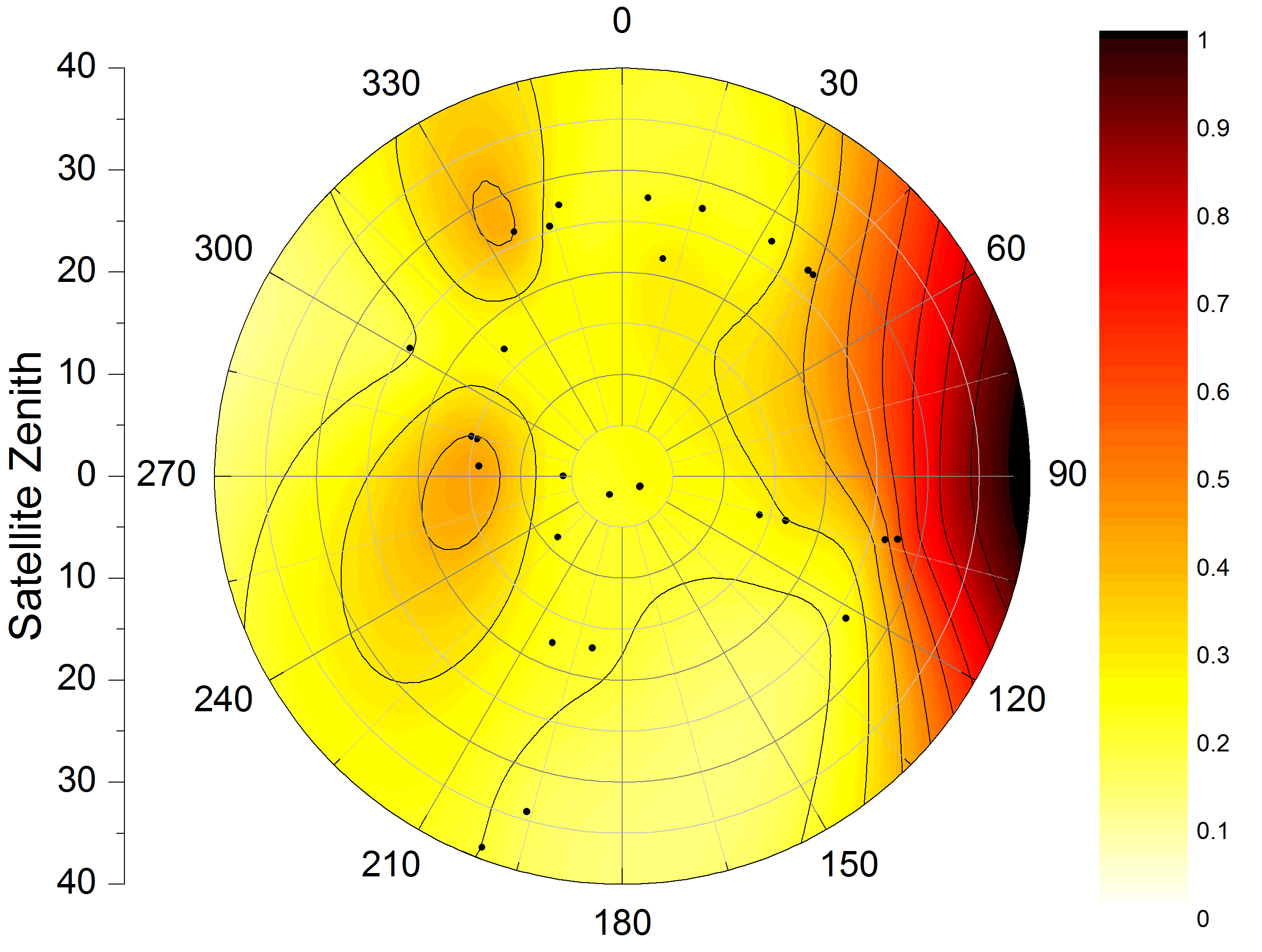
моя ближайшая попытка в R к этому моменту в основном:
### Convert polar -> cart
# ToDo #
### Dummy data
x = rnorm(20)
y = rnorm(20)
z = rnorm(20)
### Interpolate
library(akima)
tmp = interp(x,y,z)
### Plot interpolation
library(fields)
image.plot(tmp)
### ToDo ###
#Turn off all axis
#Plot polar axis ontop
, который производит что-то вроде:
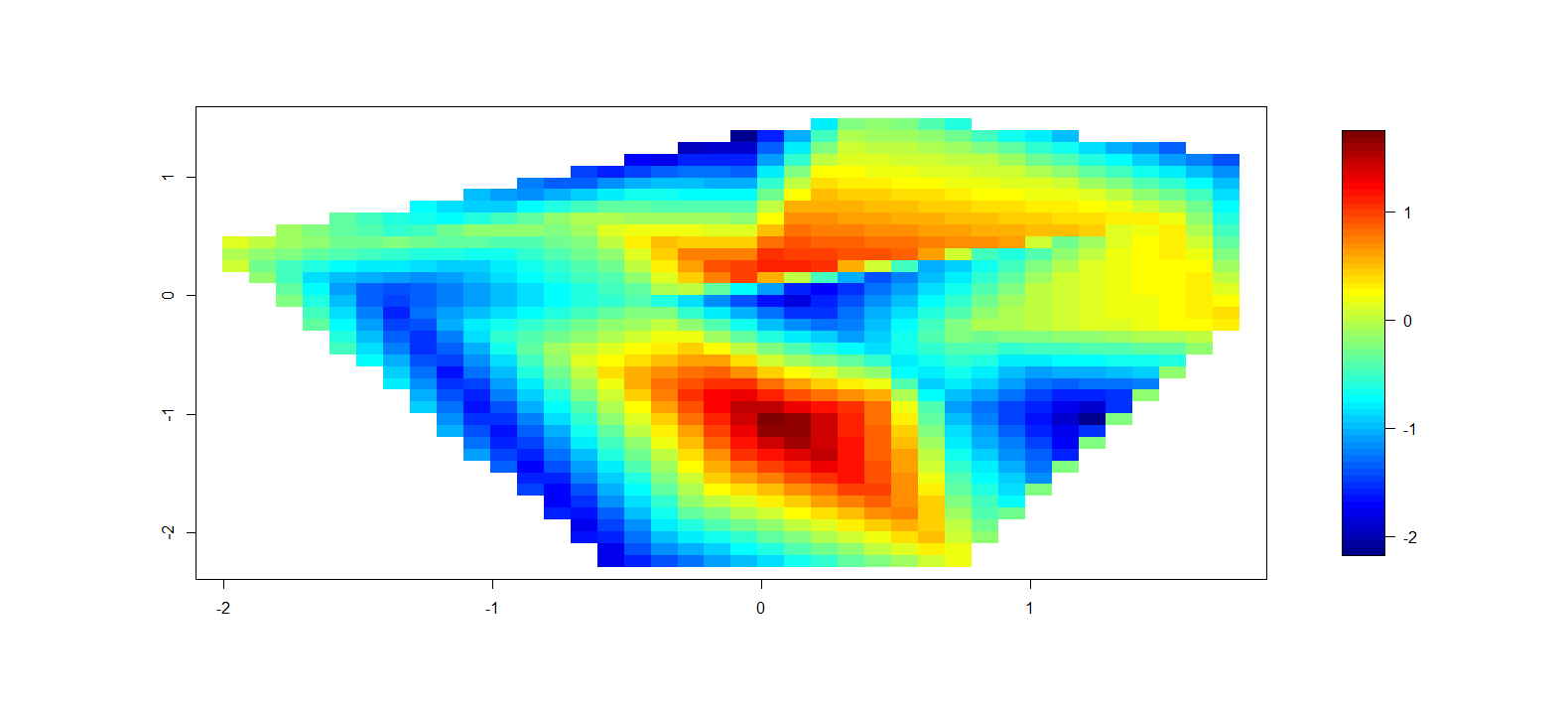
пока это очевидно, что это не будет конечным продуктом, это лучший способ создать контурные полярные участки в R?
Я не могу найти ничего по этой теме кроме архив списка рассылки дискуссия с 2008. Я думаю, что я не полностью посвящен использованию R для графиков (хотя у меня есть данные), но я против ручного создания. Итак, если есть другой язык с этой возможностью, пожалуйста, предложите его (я видел Python пример).
редактировать
Что касается предложения с использованием ggplot2 - я не могу получить процедуру geom_tile для построения интерполированных данных в polar_coordinates. Я включил код ниже, который иллюстрирует, где я нахожусь. Я могу построить оригинал в декартовом и Полярном, но я могу получить только интерполированные данные для построения в декартовом. Я могу построить точки интерполяции в polar с помощью geom_point, но я не могу расширить этот подход до geom_tile. Я только предполагал, что это связано с порядком данных - т. е. geom_tile ожидает отсортированных / упорядоченных данных - я пробовал каждую итерацию, которую я могу подумать о сортировке данных по восходящему / нисходящему азимуту и Зениту без изменений.
## Libs
library(akima)
library(ggplot2)
## Sample data in az/el(zenith)
tmp = seq(5,355,by=10)
geoms <- data.frame(az = tmp,
zen = runif(length(tmp)),
value = runif(length(tmp)))
geoms$az_rad = geoms$az*pi/180
## These points plot fine
ggplot(geoms)+geom_point(aes(az,zen,colour=value))+
coord_polar()+
scale_x_continuous(breaks=c(0,45,90,135,180,225,270,315,360),limits=c(0,360))+
scale_colour_gradient(breaks=seq(0,1,by=.1),low="black",high="white")
## Need to interpolate - most easily done in cartesian
x = geoms$zen*sin(geoms$az_rad)
y = geoms$zen*cos(geoms$az_rad)
df.ptsc = data.frame(x=x,y=y,z=geoms$value)
intc = interp(x,y,geoms$value,
xo=seq(min(x), max(x), length = 100),
yo=seq(min(y), max(y), length = 100),linear=FALSE)
df.intc = data.frame(expand.grid(x=intc$x,y=intc$y),
z=c(intc$z),value=cut((intc$z),breaks=seq(0,1,.1)))
## This plots fine in cartesian coords
ggplot(df.intc)+scale_x_continuous(limits=c(-1.1,1.1))+
scale_y_continuous(limits=c(-1.1,1.1))+
geom_point(data=df.ptsc,aes(x,y,colour=z))+
scale_colour_gradient(breaks=seq(0,1,by=.1),low="white",high="red")
ggplot(df.intc)+geom_tile(aes(x,y,fill=z))+
scale_x_continuous(limits=c(-1.1,1.1))+
scale_y_continuous(limits=c(-1.1,1.1))+
geom_point(data=df.ptsc,aes(x,y,colour=z))+
scale_colour_gradient(breaks=seq(0,1,by=.1),low="white",high="red")
## Convert back to polar
int_az = atan2(df.intc$x,df.intc$y)
int_az = int_az*180/pi
int_az = unlist(lapply(int_az,function(x){if(x<0){x+360}else{x}}))
int_zen = sqrt(df.intc$x^2+df.intc$y^2)
df.intp = data.frame(az=int_az,zen=int_zen,z=df.intc$z,value=df.intc$value)
## Just to check
az = atan2(x,y)
az = az*180/pi
az = unlist(lapply(az,function(x){if(x<0){x+360}else{x}}))
zen = sqrt(x^2+y^2)
## The conversion looks correct [[az = geoms$az, zen = geoms$zen]]
## This plots the interpolated locations
ggplot(df.intp)+geom_point(aes(az,zen))+coord_polar()
## This doesn't track to geom_tile
ggplot(df.intp)+geom_tile(aes(az,zen,fill=value))+coord_polar()
Окончательные Результаты
я, наконец, взял код из принятого ответа (основа графика) и обновил код. Я добавил метод интерполяции сплайнов тонкой пластины, возможность экстраполировать или нет, наложение точек данных и возможность делать непрерывные цвета или сегментированные цвета для интерполированной поверхности. См. примеры ниже.
PolarImageInterpolate <- function(
### Plotting data (in cartesian) - will be converted to polar space.
x, y, z,
### Plot component flags
contours=TRUE, # Add contours to the plotted surface
legend=TRUE, # Plot a surface data legend?
axes=TRUE, # Plot axes?
points=TRUE, # Plot individual data points
extrapolate=FALSE, # Should we extrapolate outside data points?
### Data splitting params for color scale and contours
col_breaks_source = 1, # Where to calculate the color brakes from (1=data,2=surface)
# If you know the levels, input directly (i.e. c(0,1))
col_levels = 10, # Number of color levels to use - must match length(col) if
#col specified separately
col = rev(heat.colors(col_levels)), # Colors to plot
contour_breaks_source = 1, # 1=z data, 2=calculated surface data
# If you know the levels, input directly (i.e. c(0,1))
contour_levels = col_levels+1, # One more contour break than col_levels (must be
# specified correctly if done manually
### Plotting params
outer.radius = round_any(max(sqrt(x^2+y^2)),5,f=ceiling),
circle.rads = pretty(c(0,outer.radius)), #Radius lines
spatial_res=1000, #Resolution of fitted surface
single_point_overlay=0, #Overlay "key" data point with square
#(0 = No, Other = number of pt)
### Fitting parameters
interp.type = 1, #1 = linear, 2 = Thin plate spline
lambda=0){ #Used only when interp.type = 2
minitics <- seq(-outer.radius, outer.radius, length.out = spatial_res)
# interpolate the data
if (interp.type ==1 ){
Interp <- akima:::interp(x = x, y = y, z = z,
extrap = extrapolate,
xo = minitics,
yo = minitics,
linear = FALSE)
Mat <- Interp[[3]]
}
else if (interp.type == 2){
library(fields)
grid.list = list(x=minitics,y=minitics)
t = Tps(cbind(x,y),z,lambda=lambda)
tmp = predict.surface(t,grid.list,extrap=extrapolate)
Mat = tmp$z
}
else {stop("interp.type value not valid")}
# mark cells outside circle as NA
markNA <- matrix(minitics, ncol = spatial_res, nrow = spatial_res)
Mat[!sqrt(markNA ^ 2 + t(markNA) ^ 2) < outer.radius] <- NA
### Set contour_breaks based on requested source
if ((length(contour_breaks_source == 1)) & (contour_breaks_source[1] == 1)){
contour_breaks = seq(min(z,na.rm=TRUE),max(z,na.rm=TRUE),
by=(max(z,na.rm=TRUE)-min(z,na.rm=TRUE))/(contour_levels-1))
}
else if ((length(contour_breaks_source == 1)) & (contour_breaks_source[1] == 2)){
contour_breaks = seq(min(Mat,na.rm=TRUE),max(Mat,na.rm=TRUE),
by=(max(Mat,na.rm=TRUE)-min(Mat,na.rm=TRUE))/(contour_levels-1))
}
else if ((length(contour_breaks_source) == 2) & (is.numeric(contour_breaks_source))){
contour_breaks = pretty(contour_breaks_source,n=contour_levels)
contour_breaks = seq(contour_breaks_source[1],contour_breaks_source[2],
by=(contour_breaks_source[2]-contour_breaks_source[1])/(contour_levels-1))
}
else {stop("Invalid selection for "contour_breaks_source"")}
### Set color breaks based on requested source
if ((length(col_breaks_source) == 1) & (col_breaks_source[1] == 1))
{zlim=c(min(z,na.rm=TRUE),max(z,na.rm=TRUE))}
else if ((length(col_breaks_source) == 1) & (col_breaks_source[1] == 2))
{zlim=c(min(Mat,na.rm=TRUE),max(Mat,na.rm=TRUE))}
else if ((length(col_breaks_source) == 2) & (is.numeric(col_breaks_source)))
{zlim=col_breaks_source}
else {stop("Invalid selection for "col_breaks_source"")}
# begin plot
Mat_plot = Mat
Mat_plot[which(Mat_plot<zlim[1])]=zlim[1]
Mat_plot[which(Mat_plot>zlim[2])]=zlim[2]
image(x = minitics, y = minitics, Mat_plot , useRaster = TRUE, asp = 1, axes = FALSE, xlab = "", ylab = "", zlim = zlim, col = col)
# add contours if desired
if (contours){
CL <- contourLines(x = minitics, y = minitics, Mat, levels = contour_breaks)
A <- lapply(CL, function(xy){
lines(xy$x, xy$y, col = gray(.2), lwd = .5)
})
}
# add interpolated point if desired
if (points){
points(x,y,pch=4)
}
# add overlay point (used for trained image marking) if desired
if (single_point_overlay!=0){
points(x[single_point_overlay],y[single_point_overlay],pch=0)
}
# add radial axes if desired
if (axes){
# internals for axis markup
RMat <- function(radians){
matrix(c(cos(radians), sin(radians), -sin(radians), cos(radians)), ncol = 2)
}
circle <- function(x, y, rad = 1, nvert = 500){
rads <- seq(0,2*pi,length.out = nvert)
xcoords <- cos(rads) * rad + x
ycoords <- sin(rads) * rad + y
cbind(xcoords, ycoords)
}
# draw circles
if (missing(circle.rads)){
circle.rads <- pretty(c(0,outer.radius))
}
for (i in circle.rads){
lines(circle(0, 0, i), col = "#66666650")
}
# put on radial spoke axes:
axis.rads <- c(0, pi / 6, pi / 3, pi / 2, 2 * pi / 3, 5 * pi / 6)
r.labs <- c(90, 60, 30, 0, 330, 300)
l.labs <- c(270, 240, 210, 180, 150, 120)
for (i in 1:length(axis.rads)){
endpoints <- zapsmall(c(RMat(axis.rads[i]) %*% matrix(c(1, 0, -1, 0) * outer.radius,ncol = 2)))
segments(endpoints[1], endpoints[2], endpoints[3], endpoints[4], col = "#66666650")
endpoints <- c(RMat(axis.rads[i]) %*% matrix(c(1.1, 0, -1.1, 0) * outer.radius, ncol = 2))
lab1 <- bquote(.(r.labs[i]) * degree)
lab2 <- bquote(.(l.labs[i]) * degree)
text(endpoints[1], endpoints[2], lab1, xpd = TRUE)
text(endpoints[3], endpoints[4], lab2, xpd = TRUE)
}
axis(2, pos = -1.25 * outer.radius, at = sort(union(circle.rads,-circle.rads)), labels = NA)
text( -1.26 * outer.radius, sort(union(circle.rads, -circle.rads)),sort(union(circle.rads, -circle.rads)), xpd = TRUE, pos = 2)
}
# add legend if desired
# this could be sloppy if there are lots of breaks, and that's why it's optional.
# another option would be to use fields:::image.plot(), using only the legend.
# There's an example for how to do so in its documentation
if (legend){
library(fields)
image.plot(legend.only=TRUE, smallplot=c(.78,.82,.1,.8), col=col, zlim=zlim)
# ylevs <- seq(-outer.radius, outer.radius, length = contour_levels+ 1)
# #ylevs <- seq(-outer.radius, outer.radius, length = length(contour_breaks))
# rect(1.2 * outer.radius, ylevs[1:(length(ylevs) - 1)], 1.3 * outer.radius, ylevs[2:length(ylevs)], col = col, border = NA, xpd = TRUE)
# rect(1.2 * outer.radius, min(ylevs), 1.3 * outer.radius, max(ylevs), border = "#66666650", xpd = TRUE)
# text(1.3 * outer.radius, ylevs[seq(1,length(ylevs),length.out=length(contour_breaks))],round(contour_breaks, 1), pos = 4, xpd = TRUE)
}
}
2 ответов
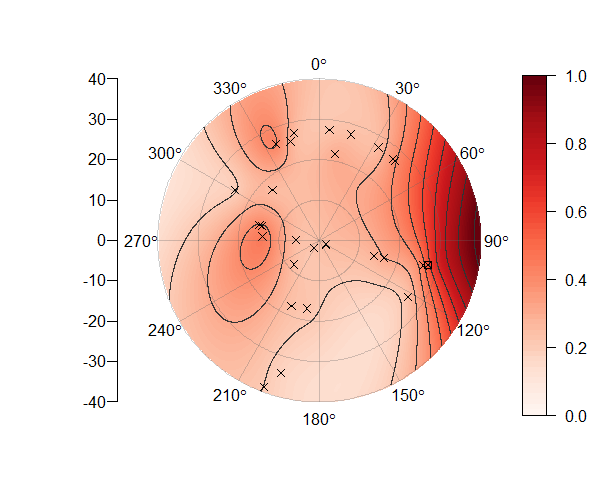
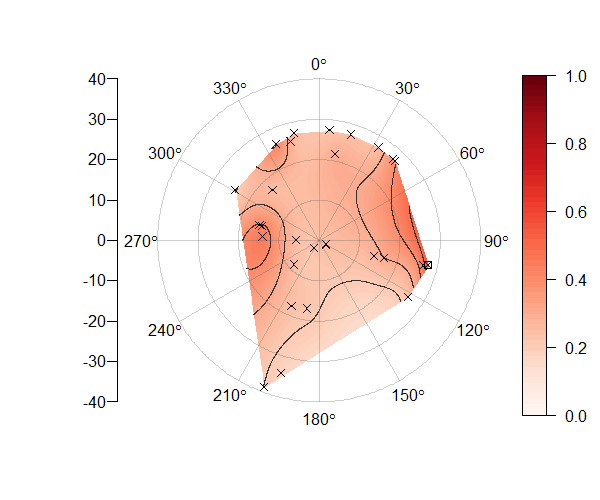
[[основные изменения]] Я, наконец, смог добавить контурные линии к моей первоначальной попытке, но поскольку две стороны исходной матрицы, которая искажается, фактически не касаются, линии не совпадают между 360 и 0 градусами. Поэтому я полностью переосмыслил проблему, но оставил исходный пост ниже, потому что все еще было здорово построить матрицу таким образом. Функция, которую я публикую сейчас, принимает x, y, z и несколько дополнительных аргументов и выплевывает что-то чертовски похожее на желаемое примеры, радиальные оси, легенда, контурные линии и все:
PolarImageInterpolate <- function(x, y, z, outer.radius = 1,
breaks, col, nlevels = 20, contours = TRUE, legend = TRUE,
axes = TRUE, circle.rads = pretty(c(0,outer.radius))){
minitics <- seq(-outer.radius, outer.radius, length.out = 1000)
# interpolate the data
Interp <- akima:::interp(x = x, y = y, z = z,
extrap = TRUE,
xo = minitics,
yo = minitics,
linear = FALSE)
Mat <- Interp[[3]]
# mark cells outside circle as NA
markNA <- matrix(minitics, ncol = 1000, nrow = 1000)
Mat[!sqrt(markNA ^ 2 + t(markNA) ^ 2) < outer.radius] <- NA
# sort out colors and breaks:
if (!missing(breaks) & !missing(col)){
if (length(breaks) - length(col) != 1){
stop("breaks must be 1 element longer than cols")
}
}
if (missing(breaks) & !missing(col)){
breaks <- seq(min(Mat,na.rm = TRUE), max(Mat, na.rm = TRUE), length = length(col) + 1)
nlevels <- length(breaks) - 1
}
if (missing(col) & !missing(breaks)){
col <- rev(heat.colors(length(breaks) - 1))
nlevels <- length(breaks) - 1
}
if (missing(breaks) & missing(col)){
breaks <- seq(min(Mat,na.rm = TRUE), max(Mat, na.rm = TRUE), length = nlevels + 1)
col <- rev(heat.colors(nlevels))
}
# if legend desired, it goes on the right and some space is needed
if (legend) {
par(mai = c(1,1,1.5,1.5))
}
# begin plot
image(x = minitics, y = minitics, t(Mat), useRaster = TRUE, asp = 1,
axes = FALSE, xlab = "", ylab = "", col = col, breaks = breaks)
# add contours if desired
if (contours){
CL <- contourLines(x = minitics, y = minitics, t(Mat), levels = breaks)
A <- lapply(CL, function(xy){
lines(xy$x, xy$y, col = gray(.2), lwd = .5)
})
}
# add radial axes if desired
if (axes){
# internals for axis markup
RMat <- function(radians){
matrix(c(cos(radians), sin(radians), -sin(radians), cos(radians)), ncol = 2)
}
circle <- function(x, y, rad = 1, nvert = 500){
rads <- seq(0,2*pi,length.out = nvert)
xcoords <- cos(rads) * rad + x
ycoords <- sin(rads) * rad + y
cbind(xcoords, ycoords)
}
# draw circles
if (missing(circle.rads)){
circle.rads <- pretty(c(0,outer.radius))
}
for (i in circle.rads){
lines(circle(0, 0, i), col = "#66666650")
}
# put on radial spoke axes:
axis.rads <- c(0, pi / 6, pi / 3, pi / 2, 2 * pi / 3, 5 * pi / 6)
r.labs <- c(90, 60, 30, 0, 330, 300)
l.labs <- c(270, 240, 210, 180, 150, 120)
for (i in 1:length(axis.rads)){
endpoints <- zapsmall(c(RMat(axis.rads[i]) %*% matrix(c(1, 0, -1, 0) * outer.radius,ncol = 2)))
segments(endpoints[1], endpoints[2], endpoints[3], endpoints[4], col = "#66666650")
endpoints <- c(RMat(axis.rads[i]) %*% matrix(c(1.1, 0, -1.1, 0) * outer.radius, ncol = 2))
lab1 <- bquote(.(r.labs[i]) * degree)
lab2 <- bquote(.(l.labs[i]) * degree)
text(endpoints[1], endpoints[2], lab1, xpd = TRUE)
text(endpoints[3], endpoints[4], lab2, xpd = TRUE)
}
axis(2, pos = -1.2 * outer.radius, at = sort(union(circle.rads,-circle.rads)), labels = NA)
text( -1.21 * outer.radius, sort(union(circle.rads, -circle.rads)),sort(union(circle.rads, -circle.rads)), xpd = TRUE, pos = 2)
}
# add legend if desired
# this could be sloppy if there are lots of breaks, and that's why it's optional.
# another option would be to use fields:::image.plot(), using only the legend.
# There's an example for how to do so in its documentation
if (legend){
ylevs <- seq(-outer.radius, outer.radius, length = nlevels + 1)
rect(1.2 * outer.radius, ylevs[1:(length(ylevs) - 1)], 1.3 * outer.radius, ylevs[2:length(ylevs)], col = col, border = NA, xpd = TRUE)
rect(1.2 * outer.radius, min(ylevs), 1.3 * outer.radius, max(ylevs), border = "#66666650", xpd = TRUE)
text(1.3 * outer.radius, ylevs,round(breaks, 1), pos = 4, xpd = TRUE)
}
}
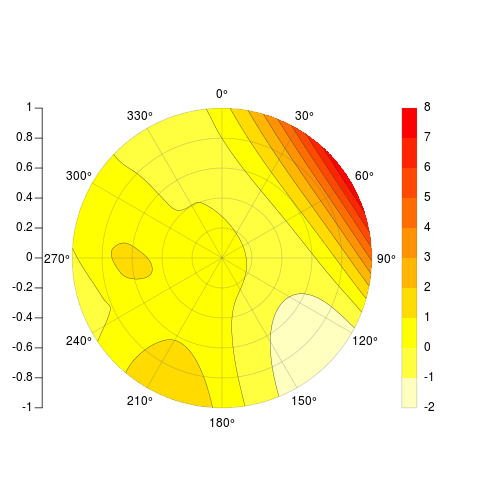
# Example
set.seed(10)
x <- rnorm(20)
y <- rnorm(20)
z <- rnorm(20)
PolarImageInterpolate(x,y,z, breaks = seq(-2,8,by = 1))
код доступен здесь: https://gist.github.com/2893780
[[мой первоначальный ответ следует]]
Я думал, что ваш вопрос будет очень познавательно для меня, поэтому я принял вызов и придумал следующую неполной функции. Он работает аналогично image(), хочет матрицу в качестве основного входа и выплевывает что-то похожее на ваш пример сверху минус контурные линии.
[[Я отредактировал код 6 июня, заметив, что он не строится в порядке, который я утверждал. Зафиксированный. В настоящее время работает над контурными линиями и легендой.]]
# arguments:
# Mat, a matrix of z values as follows:
# leftmost edge of first column = 0 degrees, rightmost edge of last column = 360 degrees
# columns are distributed in cells equally over the range 0 to 360 degrees, like a grid prior to transform
# first row is innermost circle, last row is outermost circle
# outer.radius, By default everything scaled to unit circle
# ppa: points per cell per arc. If your matrix is little, make it larger for a nice curve
# cols: color vector. default = rev(heat.colors(length(breaks)-1))
# breaks: manual breaks for colors. defaults to seq(min(Mat),max(Mat),length=nbreaks)
# nbreaks: how many color levels are desired?
# axes: should circular and radial axes be drawn? radial axes are drawn at 30 degree intervals only- this could be made more flexible.
# circle.rads: at which radii should circles be drawn? defaults to pretty(((0:ncol(Mat)) / ncol(Mat)) * outer.radius)
# TODO: add color strip legend.
PolarImagePlot <- function(Mat, outer.radius = 1, ppa = 5, cols, breaks, nbreaks = 51, axes = TRUE, circle.rads){
# the image prep
Mat <- Mat[, ncol(Mat):1]
radii <- ((0:ncol(Mat)) / ncol(Mat)) * outer.radius
# 5 points per arc will usually do
Npts <- ppa
# all the angles for which a vertex is needed
radians <- 2 * pi * (0:(nrow(Mat) * Npts)) / (nrow(Mat) * Npts) + pi / 2
# matrix where each row is the arc corresponding to a cell
rad.mat <- matrix(radians[-length(radians)], ncol = Npts, byrow = TRUE)[1:nrow(Mat), ]
rad.mat <- cbind(rad.mat, rad.mat[c(2:nrow(rad.mat), 1), 1])
# the x and y coords assuming radius of 1
y0 <- sin(rad.mat)
x0 <- cos(rad.mat)
# dimension markers
nc <- ncol(x0)
nr <- nrow(x0)
nl <- length(radii)
# make a copy for each radii, redimension in sick ways
x1 <- aperm( x0 %o% radii, c(1, 3, 2))
# the same, but coming back the other direction to close the polygon
x2 <- x1[, , nc:1]
#now stick together
x.array <- abind:::abind(x1[, 1:(nl - 1), ], x2[, 2:nl, ], matrix(NA, ncol = (nl - 1), nrow = nr), along = 3)
# final product, xcoords, is a single vector, in order,
# where all the x coordinates for a cell are arranged
# clockwise. cells are separated by NAs- allows a single call to polygon()
xcoords <- aperm(x.array, c(3, 1, 2))
dim(xcoords) <- c(NULL)
# repeat for y coordinates
y1 <- aperm( y0 %o% radii,c(1, 3, 2))
y2 <- y1[, , nc:1]
y.array <- abind:::abind(y1[, 1:(length(radii) - 1), ], y2[, 2:length(radii), ], matrix(NA, ncol = (length(radii) - 1), nrow = nr), along = 3)
ycoords <- aperm(y.array, c(3, 1, 2))
dim(ycoords) <- c(NULL)
# sort out colors and breaks:
if (!missing(breaks) & !missing(cols)){
if (length(breaks) - length(cols) != 1){
stop("breaks must be 1 element longer than cols")
}
}
if (missing(breaks) & !missing(cols)){
breaks <- seq(min(Mat,na.rm = TRUE), max(Mat, na.rm = TRUE), length = length(cols) + 1)
}
if (missing(cols) & !missing(breaks)){
cols <- rev(heat.colors(length(breaks) - 1))
}
if (missing(breaks) & missing(cols)){
breaks <- seq(min(Mat,na.rm = TRUE), max(Mat, na.rm = TRUE), length = nbreaks)
cols <- rev(heat.colors(length(breaks) - 1))
}
# get a color for each cell. Ugly, but it gets them in the right order
cell.cols <- as.character(cut(as.vector(Mat[nrow(Mat):1,ncol(Mat):1]), breaks = breaks, labels = cols))
# start empty plot
plot(NULL, type = "n", ylim = c(-1, 1) * outer.radius, xlim = c(-1, 1) * outer.radius, asp = 1, axes = FALSE, xlab = "", ylab = "")
# draw polygons with no borders:
polygon(xcoords, ycoords, col = cell.cols, border = NA)
if (axes){
# a couple internals for axis markup.
RMat <- function(radians){
matrix(c(cos(radians), sin(radians), -sin(radians), cos(radians)), ncol = 2)
}
circle <- function(x, y, rad = 1, nvert = 500){
rads <- seq(0,2*pi,length.out = nvert)
xcoords <- cos(rads) * rad + x
ycoords <- sin(rads) * rad + y
cbind(xcoords, ycoords)
}
# draw circles
if (missing(circle.rads)){
circle.rads <- pretty(radii)
}
for (i in circle.rads){
lines(circle(0, 0, i), col = "#66666650")
}
# put on radial spoke axes:
axis.rads <- c(0, pi / 6, pi / 3, pi / 2, 2 * pi / 3, 5 * pi / 6)
r.labs <- c(90, 60, 30, 0, 330, 300)
l.labs <- c(270, 240, 210, 180, 150, 120)
for (i in 1:length(axis.rads)){
endpoints <- zapsmall(c(RMat(axis.rads[i]) %*% matrix(c(1, 0, -1, 0) * outer.radius,ncol = 2)))
segments(endpoints[1], endpoints[2], endpoints[3], endpoints[4], col = "#66666650")
endpoints <- c(RMat(axis.rads[i]) %*% matrix(c(1.1, 0, -1.1, 0) * outer.radius, ncol = 2))
lab1 <- bquote(.(r.labs[i]) * degree)
lab2 <- bquote(.(l.labs[i]) * degree)
text(endpoints[1], endpoints[2], lab1, xpd = TRUE)
text(endpoints[3], endpoints[4], lab2, xpd = TRUE)
}
axis(2, pos = -1.2 * outer.radius, at = sort(union(circle.rads,-circle.rads)))
}
invisible(list(breaks = breaks, col = cols))
}
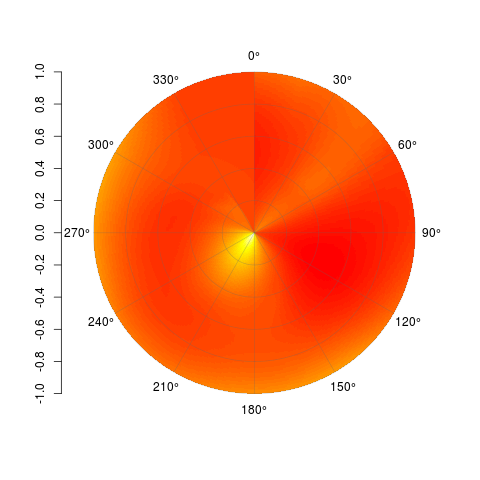
Я не знаю, как правильно интерполировать по полярной поверхности, поэтому, предполагая, что вы можете достичь этого и получить свои данные в матрицу, эта функция получит ее для вас. Каждая ячейка рисуется, как с image(), но внутренние из них крошечные. Вот пример:
set.seed(1)
x <- runif(20, min = 0, max = 360)
y <- runif(20, min = 0, max = 40)
z <- rnorm(20)
Interp <- akima:::interp(x = x, y = y, z = z,
extrap = TRUE,
xo = seq(0, 360, length.out = 300),
yo = seq(0, 40, length.out = 100),
linear = FALSE)
Mat <- Interp[[3]]
PolarImagePlot(Mat)
во что бы то ни стало, не стесняйтесь изменять это и делать с этим, что хотите. Код доступен на Github здесь:https://gist.github.com/2877281
Целевого Участка
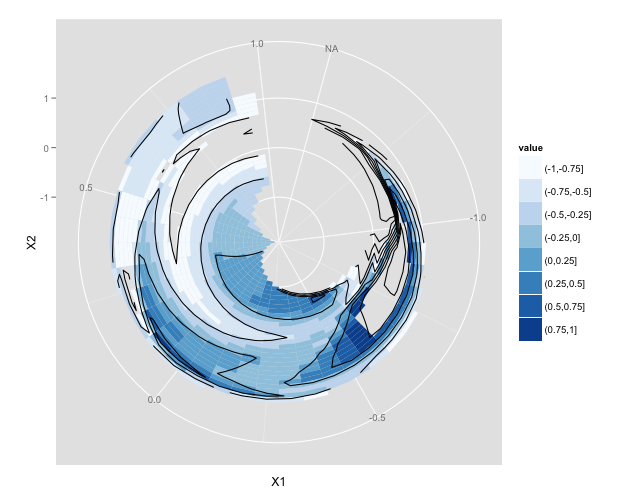
Пример Кода
library(akima)
library(ggplot2)
x = rnorm(20)
y = rnorm(20)
z = rnorm(20)
t. = interp(x,y,z)
t.df <- data.frame(t.)
gt <- data.frame( expand.grid(X1=t.$x,
X2=t.$y),
z=c(t.$z),
value=cut(c(t.$z),
breaks=seq(-1,1,0.25)))
p <- ggplot(gt) +
geom_tile(aes(X1,X2,fill=value)) +
geom_contour(aes(x=X1,y=X2,z=z), colour="black") +
coord_polar()
p <- p + scale_fill_brewer()
p
ggplot2 затем имеет много вариантов для изучения цветовых шкал re, аннотаций и т. д. но это должно помочь тебе начать.
кредит этот ответ Андри Де Фриза это привело меня к этому решению.
