R: вычислить и интерпретировать коэффициент шансов в логистической регрессии

коэффициент, возвращаемый логистической регрессией в r, является логитом или журналом шансов. Для преобразования логитов в отношение шансов, вы можете возведение ее в степень, как вы сделали выше. Для преобразования логитов в вероятности можно использовать функцию exp(logit)/(1+exp(logit)). Однако, есть некоторые вещи, чтобы отметить об этой процедуре.

во-первых, я буду использовать некоторые воспроизводимые данные для иллюстрации

library('MASS')
data("menarche")
m<-glm(cbind(Menarche, Total-Menarche) ~ Age, family=binomial, data=menarche)
summary(m)

возвращает:

Call:
glm(formula = cbind(Menarche, Total - Menarche) ~ Age, family = binomial, 
    data = menarche)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.0363  -0.9953  -0.4900   0.7780   1.3675  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -21.22639    0.77068  -27.54   <2e-16 ***
Age           1.63197    0.05895   27.68   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 3693.884  on 24  degrees of freedom
Residual deviance:   26.703  on 23  degrees of freedom
AIC: 114.76

Number of Fisher Scoring iterations: 4

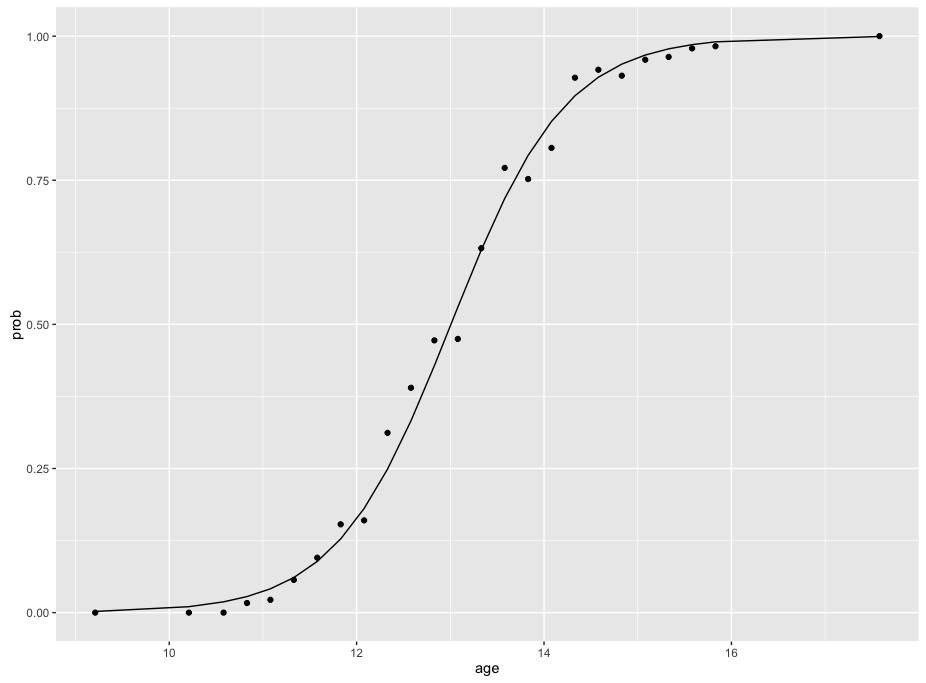
коэффициенты, отображаемые для логитов, просто как в твоем примере. Если мы построим эти данные и эту модель, мы увидим сигмоидальную функцию, характерную для логистической модели, соответствующей биномиальным данным

#predict gives the predicted value in terms of logits
plot.dat <- data.frame(prob = menarche$Menarche/menarche$Total,
                       age = menarche$Age,
                       fit = predict(m, menarche))
#convert those logit values to probabilities
plot.dat$fit_prob <- exp(plot.dat$fit)/(1+exp(plot.dat$fit))

library(ggplot2)
ggplot(plot.dat, aes(x=age, y=prob)) + 
  geom_point() +
  geom_line(aes(x=age, y=fit_prob))

обратите внимание, что изменение вероятностей не является постоянным - кривая сначала поднимается медленно, затем быстрее в середине, а затем выравнивается в конце. Разница в вероятностях между 10 и 12 гораздо меньше, чем разница в вероятностях между 12 и 14. Этот это означает, что невозможно суммировать соотношение возраста и вероятностей с одним числом без преобразования вероятностей.

чтобы ответить на ваши конкретные вопросы:

как вы интерпретируете отношения шансов?

отношение шансов для значения перехвата-это шансы на "успех" (в ваших данных это шансы взять продукт), когда x = 0 (т. е. нулевые мысли). Коэффициент шансов для вашего коэффициента-это увеличение шансов выше этого значения то перехватить, когда вы добавляете одно целое значение x (т. е. x=1; одна мысль). Используя данные menarche:

exp(coef(m))

 (Intercept)          Age 
6.046358e-10 5.113931e+00 

мы могли бы интерпретировать это как вероятность того, что менархе произойдет в возрасте = 0 .00000000006. Или, в принципе невозможно. Exponentiating возрастной коэффициент говорит нам ожидаемое увеличение шансов менархе для каждой единицы времени. В данном случае, это просто более quintupling. Коэффициент шансов 1 указывает на отсутствие изменений, в то время как коэффициент шансов 2 указывает на удвоение, так далее.

ваш коэффициент шансов 2,07 означает, что увеличение на 1 единицу "мыслей" увеличивает шансы взять продукт в 2,07 раза.

как вы конвертируете соотношение шансов мыслей в оценочную вероятность решения?

вам нужно сделать это для выбранных значений мыслей, потому что, как вы можете видеть на графике выше, изменение не является постоянным в диапазоне значений X. Если вы хотите вероятность некоторого значения для мысли, получить ответ следующим образом:

exp(intercept + coef*THOUGHT_Value)/(1+(exp(intercept+coef*THOUGHT_Value))