Расчет цикломатической сложности [закрыто]
Я нахожусь на стадии обучения цикломатической сложности (CC). Для практики я вычисляю цикломатическую сложность 2 примеров и хочу подтвердить, правильны ли мои ответы или нет...
ссылаясь на Википедию, CC дается M = E − N + 2P где:
- E = количество ребер графика
- N = количество узлов графа
- P = количество подключенных компонентов
пожалуйста помощь.
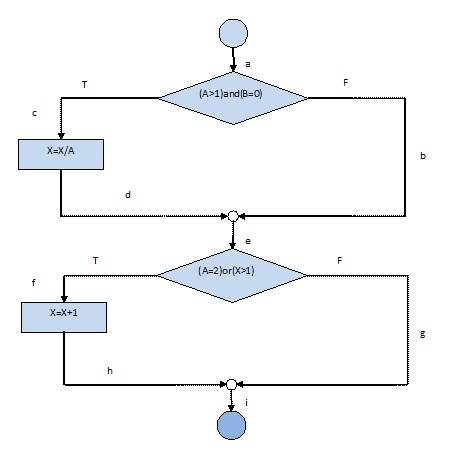
здесь E = 8, N = 9 и P = 1. Следовательно, M = 8-9 + (2x1) = 1.
Пример 2:
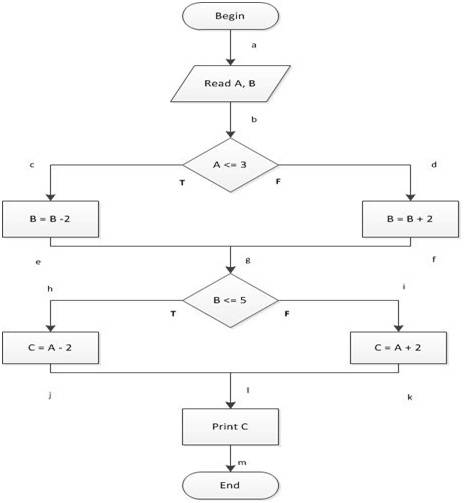
здесь E = 11, N = 10 и P = 1. Следовательно, M = 10-11 + (2x1) = 1.
следовательно, для обоих примеров CC равен 1. Пожалуйста, дайте мне знать, если мои расчеты верны или нет.
4 ответов
вам нужно позаботиться о том, чтобы правильно вставить значения в Формулу.
в Примере 1, Вы говорите
здесь, E = 8, N = 9 и P = 1
но на самом деле это наоборот: 9 ребер (=E), 8 узлов (=N), поэтому вы получаете CC 3.
в Примере 2 у вас есть правильные значения: E=11, N=10, P=1. Но вы вставляете их в неправильном порядке в Формулу; на самом деле это должно быть 11 - 10 + (2x1) = 3.
ярлык: если у вас есть изображение вашего графика, вы можете очень легко определить цикломатическую сложность. Просто подсчитайте количество областей, на которые фон разделен ребрами. В первом примере у вас есть 2 внутренние области (граничащие с краями) и одна окружающая область, дающая CC 3. То же самое относится и ко второму примеру. (Этот метод требует, чтобы ребра не пересекались друг с другом, очевидно.)
также, если это помогает, это число условных (If, while, for) операторов +1. Так в приведенном выше примере, есть 2 условных операторов . так что 2+1=3. Цикломатическая сложность в этом случае составляет 3
просто подсчитайте количество закрытых областей и добавьте к ним 1.
в вашем примере выше количество закрытых областей = 2, поэтому CC = 2+1 = 3
