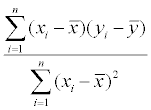Расчет наклонов в Numpy (или Scipy)
Я пытаюсь найти самый быстрый и эффективный способ расчета склонов с помощью Numpy и Scipy. У меня есть набор данных из трех переменных Y и одной переменной X, и мне нужно рассчитать их отдельные склоны. Например, я могу легко сделать это по одной строке за раз, как показано ниже, но я надеялся, что есть более эффективный способ сделать это. Я также не думаю, что linregress-лучший способ пойти, потому что мне не нужны никакие вспомогательные переменные, такие как перехват, Стандартная ошибка и т. д. результаты. Любая помощь очень ценится.
import numpy as np
from scipy import stats
Y = [[ 2.62710000e+11 3.14454000e+11 3.63609000e+11 4.03196000e+11
4.21725000e+11 2.86698000e+11 3.32909000e+11 4.01480000e+11
4.21215000e+11 4.81202000e+11]
[ 3.11612352e+03 3.65968334e+03 4.15442691e+03 4.52470938e+03
4.65011423e+03 3.10707392e+03 3.54692896e+03 4.20656404e+03
4.34233412e+03 4.88462501e+03]
[ 2.21536396e+01 2.59098311e+01 2.97401268e+01 3.04784552e+01
3.13667639e+01 2.76377113e+01 3.27846013e+01 3.73223417e+01
3.51249997e+01 4.42563658e+01]]
X = [ 1990. 1991. 1992. 1993. 1994. 1995. 1996. 1997. 1998. 1999.]
slope_0, intercept, r_value, p_value, std_err = stats.linregress(X, Y[0,:])
slope_1, intercept, r_value, p_value, std_err = stats.linregress(X, Y[1,:])
slope_2, intercept, r_value, p_value, std_err = stats.linregress(X, Y[2,:])
slope_0 = slope/Y[0,:][0]
slope_1 = slope/Y[1,:][0]
slope_2 = slope/Y[2,:][0]
b, a = polyfit(X, Y[1,:], 1)
slope_1_a = b/Y[1,:][0]
5 ответов
расчет линейной регрессии, в одном измерении, а расчет вектора. Это означает, что мы можем объединить умножения на всю Y матрица, а затем векторизировать подходит с помощью ось параметр в numpy. В вашем случае это работает следующим
((X*Y).mean(axis=1) - X.mean()*Y.mean(axis=1)) / ((X**2).mean() - (X.mean())**2)
вас не интересуют параметры качества подгонки, но большинство из них можно получить аналогичным образом.
самый быстрый и эффективный способ-использовать собственную функцию scipy из linregress, который рассчитывает все:
slope: наклон линии регрессии
перехват : перехват линии регрессии
R-значение : коэффициент корреляции
p-value: двустороннее p-значение для теста гипотезы, нулевая гипотеза которого заключается в том, что наклон равен нулю
поток stderr : стандартный ошибка оценки
и вот пример:
a = [15, 12, 8, 8, 7, 7, 7, 6, 5, 3]
b = [10, 25, 17, 11, 13, 17, 20, 13, 9, 15]
from scipy.stats import linregress
linregress(a, b)
вернет вас:
LinregressResult(slope=0.20833333333333337, intercept=13.375, rvalue=0.14499815458068521, pvalue=0.68940144811669501, stderr=0.50261704627083648)
P. S. Это просто математическая формула для склона:
С X и Y определены так же, как в вашем вопросе, вы можете использовать:
dY = (numpy.roll(Y, -1, axis=1) - Y)[:,:-1]
dX = (numpy.roll(X, -1, axis=0) - X)[:-1]
slopes = dY/dX
numpy.roll () помогает выровнять следующее наблюдение с текущим, вам просто нужно удалить последний столбец, который не является полезной разницей между последним и первым наблюдениями. Затем вы можете рассчитать все склоны сразу, без scipy.
в вашем примере dX всегда 1, поэтому вы можете сэкономить больше времени, вычисляя slopes = dY.
представление, которое проще принятого ответа:
x = np.linspace(0, 10, 11)
y = np.linspace(0, 20, 11)
y = np.c_[y, y,y]
X = x - x.mean()
Y = y - y.mean()
slope = (X.dot(Y)) / (X.dot(X))
уравнение для наклона исходит из векторная нотация для наклона линии с использованием простой регрессии.
то, как я это сделал, использует np.дифференциал (функция):
dx = np.diff (xvals),
dy = np.diff (yvals)
склоны = dy / dx