Расчет углов между сегментами линии (Python) с помощью math.инструмент atan2

Я работаю над проблемой пространственного анализа и частью этого процесса является вычисление угла между Соединенных отрезков.

каждый сегмент линии состоит только из двух точек, и каждая точка имеет пару координат XY (декартовых). Вот изображение из GeoGebra. мне всегда интересно получить положительный угол в диапазоне от 0 до 180. Однако, я получаю все виды углов в зависимости от порядка вершин в строке ввода сегменты.

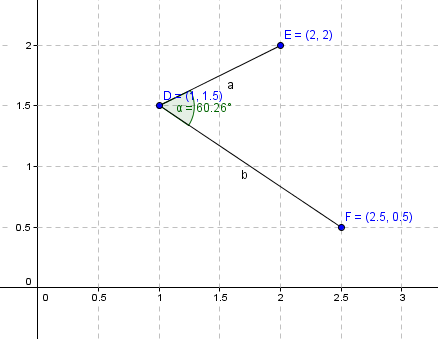
enter image description here

входные данные, с которыми я работаю, предоставляются в виде кортежей координат. В зависимости от порядка создания вершины последняя/конечная точка для каждого сегмента линии может быть разной. Вот некоторые из случаев в коде Python. Порядок сегментов линии, в котором я их получаю, является случайным, но в кортежах кортежей первый элемент является начальной точкой, а второй-конечной точкой. DE линейный сегмент, например, бы ((1,1.5),(2,2)) и (1,1.5) является начальной точкой, потому что она имеет первую позицию в кортеже координат.

мне, однако, нужно убедиться, что я получу тот же угол между DE,DF и ED,DF и так далее.

vertexType = "same start point; order 1"
            #X, Y    X Y coords
lineA = ((1,1.5),(2,2)) #DE
lineB = ((1,1.5),(2.5,0.5)) #DF
calcAngle(lineA, lineB,vertexType)
#flip lines order
vertexType = "same start point; order 2"
lineB = ((1,1.5),(2,2)) #DE
lineA = ((1,1.5),(2.5,0.5)) #DF
calcAngle(lineA, lineB,vertexType)

vertexType = "same end point; order 1"
lineA = ((2,2),(1,1.5)) #ED
lineB = ((2.5,0.5),(1,1.5)) #FE
calcAngle(lineA, lineB,vertexType)
#flip lines order
vertexType = "same end point; order 2"
lineB = ((2,2),(1,1.5)) #ED
lineA = ((2.5,0.5),(1,1.5)) #FE
calcAngle(lineA, lineB,vertexType)

vertexType = "one line after another - down; order 1"
lineA = ((2,2),(1,1.5)) #ED
lineB = ((1,1.5),(2.5,0.5)) #DF
calcAngle(lineA, lineB,vertexType)
#flip lines order
vertexType = "one line after another - down; order 2"
lineB = ((2,2),(1,1.5)) #ED
lineA = ((1,1.5),(2.5,0.5)) #DF
calcAngle(lineA, lineB,vertexType)

vertexType = "one line after another - up; line order 1"
lineA = ((1,1.5),(2,2)) #DE
lineB = ((2.5,0.5),(1,1.5)) #FD
calcAngle(lineA, lineB,vertexType)
#flip lines order
vertexType = "one line after another - up; line order 2"
lineB = ((1,1.5),(2,2)) #DE
lineA = ((2.5,0.5),(1,1.5)) #FD
calcAngle(lineA, lineB,vertexType)

я написал крошечную функцию, которая принимает комбинации линий как args и вычисляет угол между ними. Я использую math.atan2, который, казалось, лучше подходит для этого. 

def calcAngle(lineA,lineB,vertexType):
    line1Y1 = lineA[0][1]
    line1X1 = lineA[0][0]
    line1Y2 = lineA[1][1]
    line1X2 = lineA[1][0]

    line2Y1 = lineB[0][1]
    line2X1 = lineB[0][0]
    line2Y2 = lineB[1][1]
    line2X2 = lineB[1][0]

    #calculate angle between pairs of lines
    angle1 = math.atan2(line1Y1-line1Y2,line1X1-line1X2)
    angle2 = math.atan2(line2Y1-line2Y2,line2X1-line2X2)
    angleDegrees = (angle1-angle2) * 360 / (2*math.pi)
    print angleDegrees, vertexType

вывод, который я получаю:

> -299.744881297 same start point; order 1
> 299.744881297 same start point; order 2
> 60.2551187031 same end point; order 1
> -60.2551187031 same end point; order 2
> -119.744881297 one line after another - down; order 1
> 119.744881297 one line after another - down; order 2
> -119.744881297 one line after another - up; line order 1
> 119.744881297 one line after another - up; line order 2

как вы можете видите, я получаю разные значения в зависимости от порядка вершин в сегменте линии и порядок отрезков. Я попытался обработать углы, выяснив, какое отношение имела исходная линия, и перевернув линии,отредактировав угол и т. д. Я закончил с дюжиной таких случаев, и в какой-то момент они начинают перекрываться, и я больше не могу выяснить, должен ли -119.744 стать 60.255 (острый угол) или остаться как 119.744 (тупой угол) и т. д.

там любой дискретный способ обработки значений выходного угла, которые я получаю от math.atan2 получить только положительное значение в диапазоне от 0 до 180? если нет, то какой другой подход я должен принять?

6
angle atan2 cartesian-coordinates python trigonometry

2 ответов

самый простой и логичный способ решить эту проблему-использовать точечный продукт.

попробуйте этот код (я прокомментировал практически все):

import math
def dot(vA, vB):
    return vA[0]*vB[0]+vA[1]*vB[1]
def ang(lineA, lineB):
    # Get nicer vector form
    vA = [(lineA[0][0]-lineA[1][0]), (lineA[0][1]-lineA[1][1])]
    vB = [(lineB[0][0]-lineB[1][0]), (lineB[0][1]-lineB[1][1])]
    # Get dot prod
    dot_prod = dot(vA, vB)
    # Get magnitudes
    magA = dot(vA, vA)**0.5
    magB = dot(vB, vB)**0.5
    # Get cosine value
    cos_ = dot_prod/magA/magB
    # Get angle in radians and then convert to degrees
    angle = math.acos(dot_prod/magB/magA)
    # Basically doing angle <- angle mod 360
    ang_deg = math.degrees(angle)%360

    if ang_deg-180>=0:
        # As in if statement
        return 360 - ang_deg
    else: 

        return ang_deg

теперь попробуйте свои варианты lineA и lineB, и все должны дать один и тот же ответ.

6

слишком много работы. Возьмите абсолютное значение arccosine скалярное произведение из двух векторов, разделенных на каждую из длин линий.

2